←   Leptonen-Modell


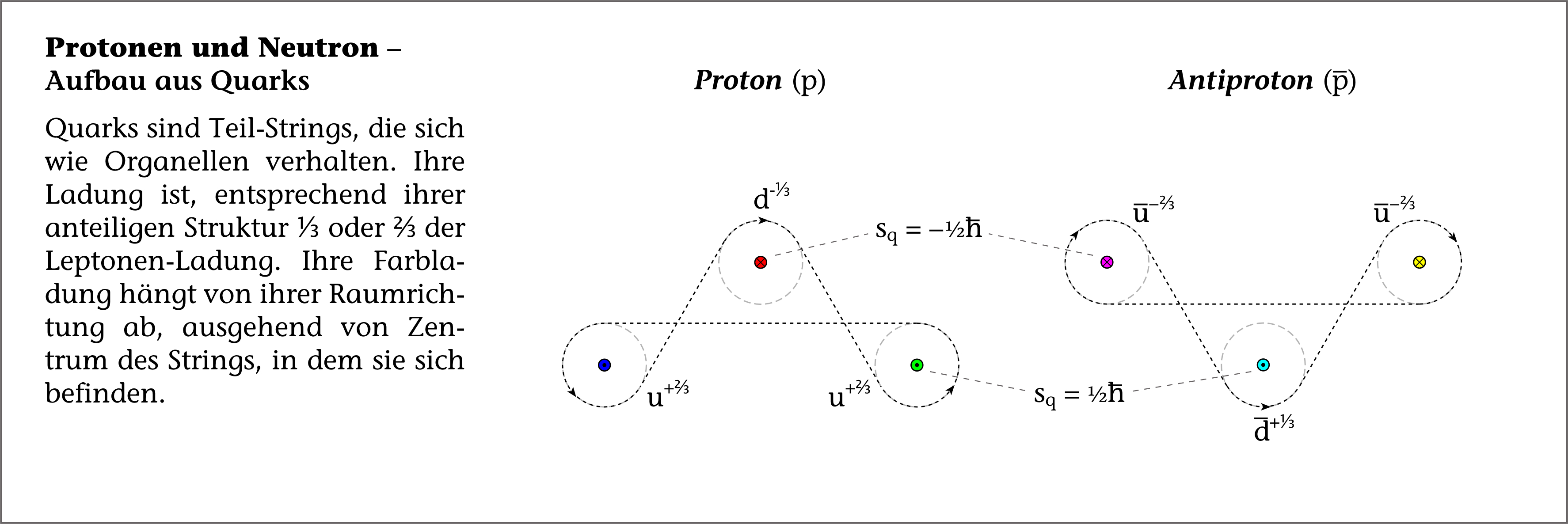
Quantenchromodynamik (Hadronen-Modell)
in der Quanten-Fluss-Theorie

Ein Symmetriebruch der Farbpolarisation des Leptonen-Wirkungsquanten-Strings bringt Quarks und Gluonen hervor


▾ Notizen

• Ein ausführlicher Artikel über die Gluonen und die Probleme der QCD findet sich in Ent, »Der Klebstoff der Welt«. Die FrQFT kann wichtige dieser Fragen, wie zum Confinement und der Gluonen-Energie, zumindestens qualitativ beantworten.
• Mesonen bestehen aus Quarks und Antiquarks. Wie arbeiten diese im String genau zusammen? Gibt es Mesonen aus allen Quark-Flavours?
Aktuelle Forschung
• Kleines elektrisches Dipolmoment des Neutrons: Kann das kleine elektrische Dipolmoment des Neutrons zur Berechnung der Wellenzahl der Leptonen benutzt werden? Siehe Sabine Hossenfelder, Vortrag in Stuttgart: Was läuft falsch in der gegenwärtigen Physik? bei Minute 48.
⋅ »Das Neutron – unverzichtbarer Bauteil aller Atomkerne mit mehr als einem Proton – ist nach außen hin zwar elektrisch neutral. Aber es setzt sich aus geladenen Bestandteilen zusammen.« (siehe Spektrum der Wissenschaft, online: Das Neutron bleibt symmetrisch)

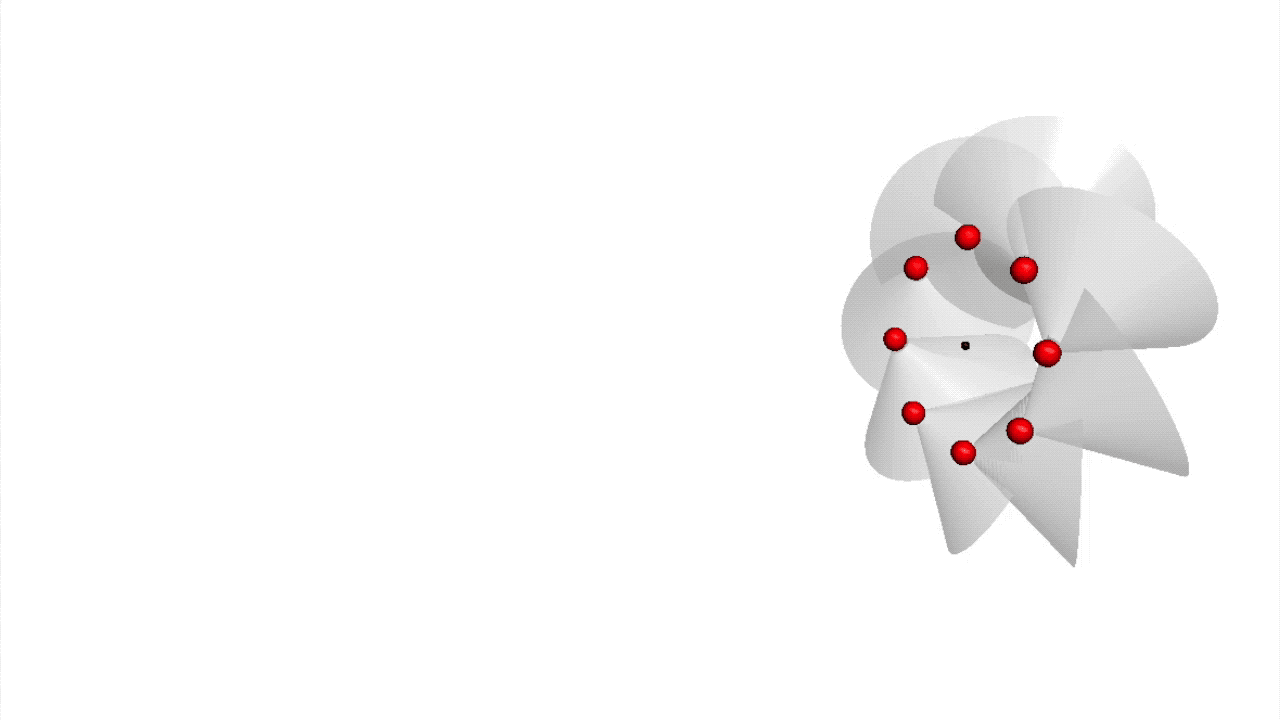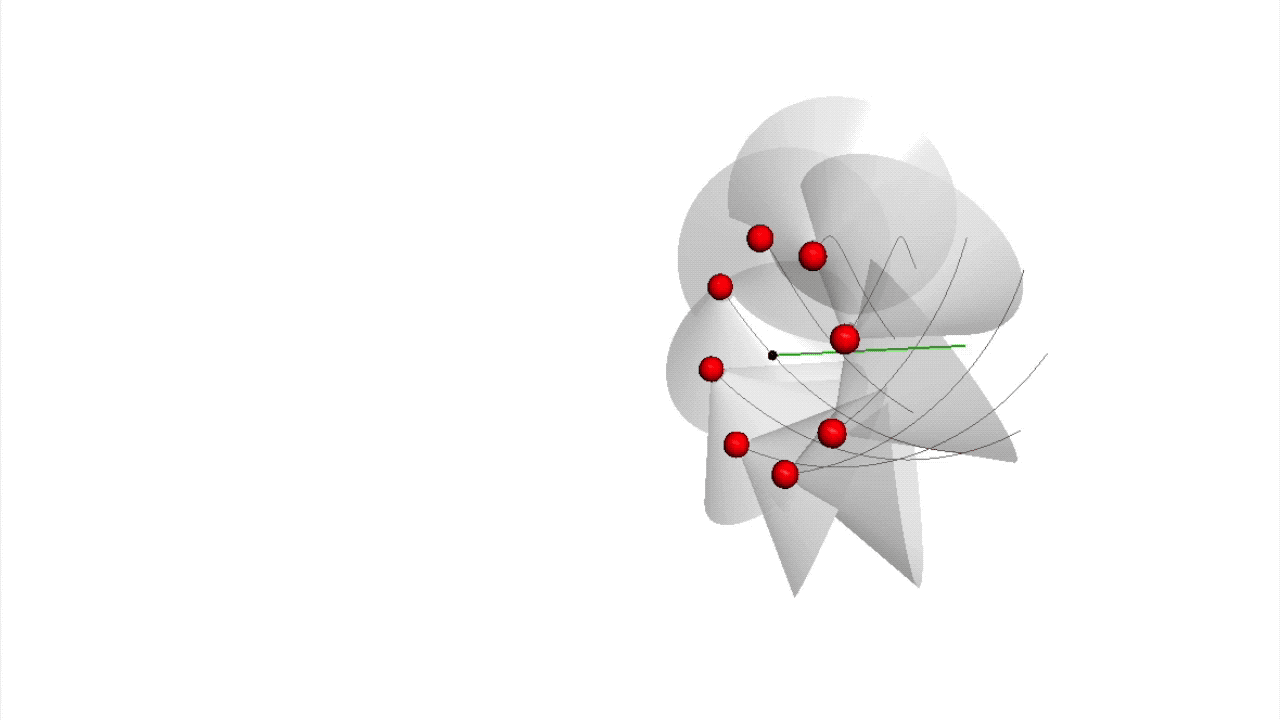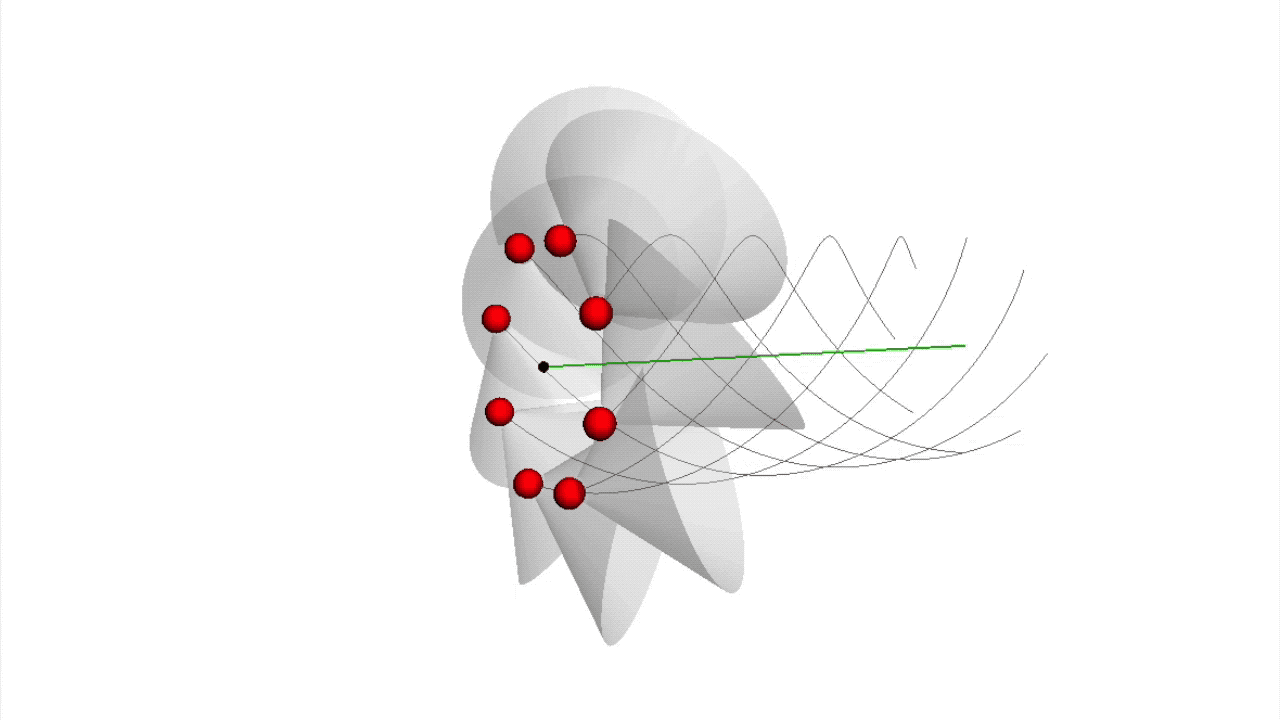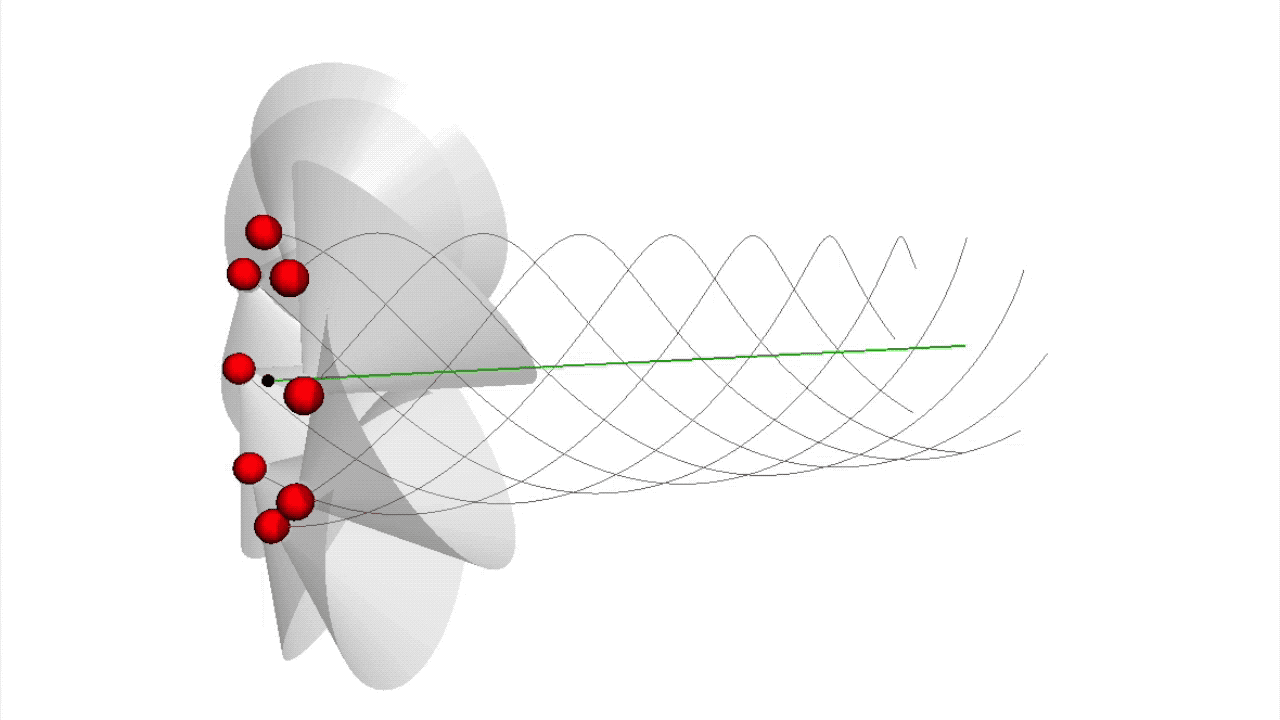
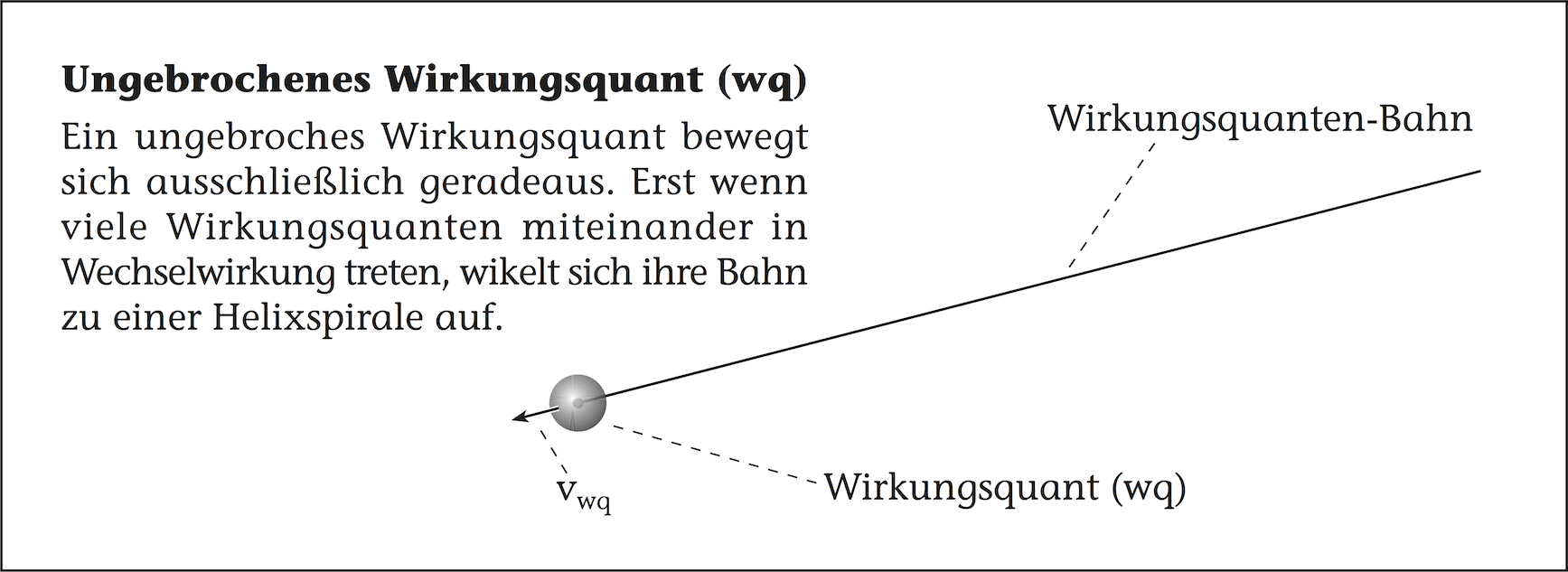
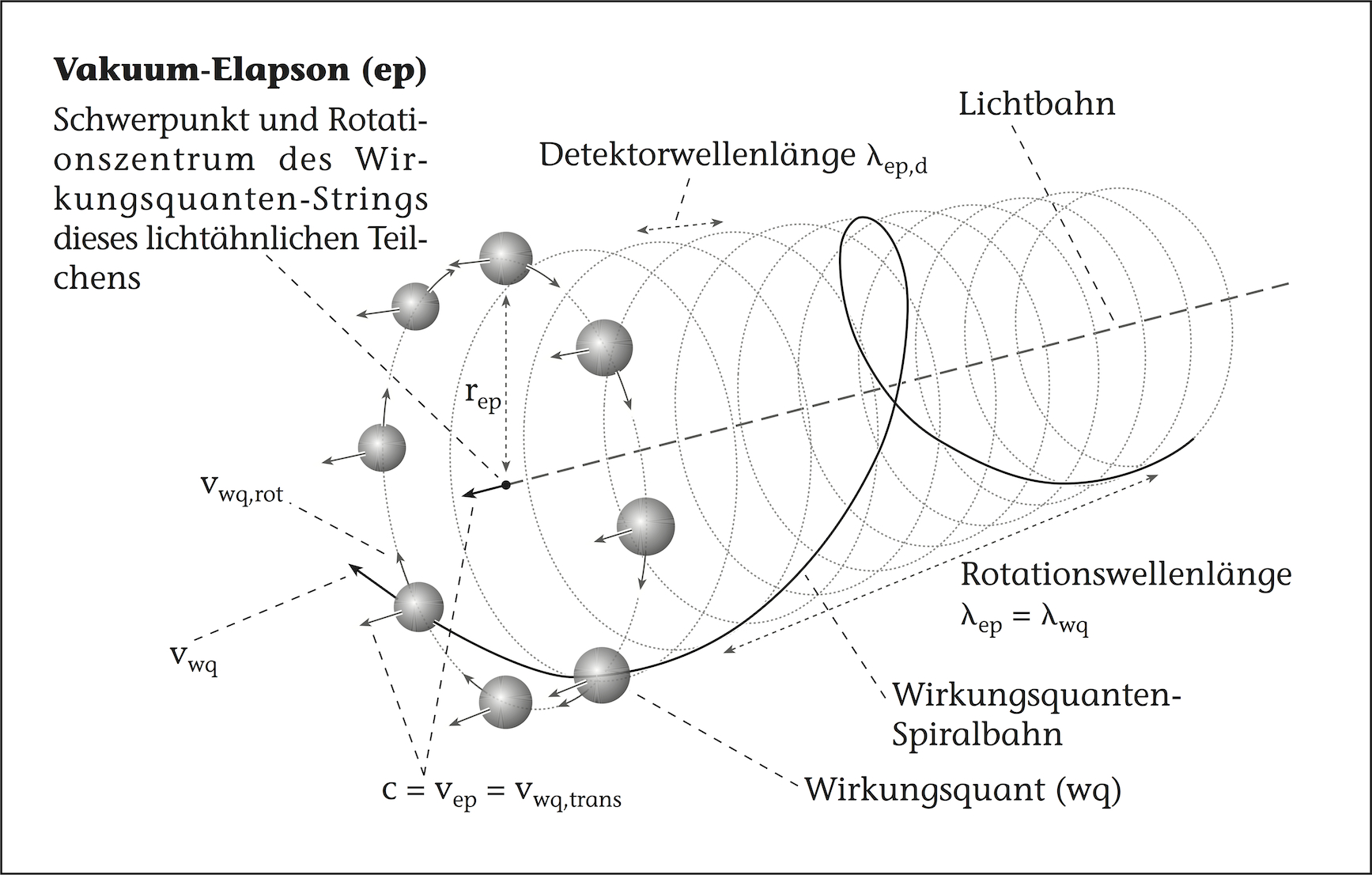
Der heutigen Quantenchromodynamik liegen die Farbladungen der und der diese verbindenden zugrunde. Bisher gibt es allerdings kein Verständnis dafür, welche physikalische Ursache die Farbladungen erzeugt. Die Wirkungsquanten-Strings der Quanten-Fluss-Theorie liefern eine neue Polarisation, auf deren Basis die Farbladungen zustande kommen. Denn die Existenz jedes Wirkungsquanten-Strings basiert auf einem fundamentalen Symmetriebruch der Bewegung der den String bildenden Wirkungsquanten. Schon im simpelsten Wirkungsquanten-String der Vakuum-Elapsonen oder beim Photonen-String kommt die Bahn der Wirkungsquanten aus ihrer symmetrischen Geradlinigkeit und wird zu einer Helixspiralbahn gebrochen.

Es ergibt sich also eine Polarisation der Bahn eines Wirkungsquants, die von der Richtung des Auslenkungswinkels und vom Auslenkungsabstand sowie von der Rotationsrichtung bestimmt ist. Diese neue Polarisation nenne ich Farbpolarisation. Die senkrecht zu ihrer Bewegungsrichtung rotierenden Vakuum-Elapsonen- und Photonen-Strings bestehen aus Wirkungsquanten, die alle in die selbe Richtung rotieren, aber von denen jedes einen anderen Brechungswinkel besitzt. Das Farbpolarisationspotenzial, das die Wirkungsquanten auf dem einfachen Kreis eines Vakuum-Elapsons hält, hat eine Sombrero-Form (siehe Abbildung XXX) und ist dem Higgs-Potenzial sehr ähnlich. Die Wirkungsquanten eines Photons werden von einem Farbpolarisationspotenzial erzeugt, das einem rotierenden, elliptischen Sombrero entspricht.

Die Summe dieser Farbpolarisationen aller Wirkungsquanten eines Vakuum-Elapsonen- und Photonen-Strings ergibt die Farbladung Weiß, also eine Eins für jede Farbpolarisationsdimension. Ebenso ergibt sich die Farbladung jedes Leptons zu Weiß.

Anders sieht es bei den Quarks und Gluonen aus: Da die Quarks ein Drittel oder zwei Drittel Leptonen sind, die zu mehreren in einem Hadronen-String sitzen, tragen sie nach innen eine Farbladung, während der Hadronen-String im ganzen nach außen und bei größerem Abstand neutral weiß erscheint. Die Gluonen sind hingegen ein Drittel oder zwei Drittel Vakuum-Elapsonen, die zu mehreren in einem Hadronen-String sitzen, und tragen daher ebenfalls eine entsprechende Farbladung. Die Gluonen rotieren sowohl um das Zentrum ihrer eigenen Teilkreisform, als auch mit dem String mit Lichtgeschwindigkeit abwechselnd durch alle Quarks des Hadrons. Dadurch ändert sich ständig ihre absolute Farbladung und auch die der Quarks auf recht komplexe Weise. Die Gluonen bewegen sich also mit Lichtgeschwindigkeit durch den Raum und sind irgendetwas zwischen Vakuum-Elapson und Photon.

Ein großes Rätsel der heutigen Physik ist das , das Eingesperrtsein der Quarks und Gluonen in den Hadronen. Doch das Confinement der Quarks und Gluonen ist eine logische Schlussfolgerung des Hadronen-Modells in der Quanten-Fluss-Theorie, wie sich nachfolgend herausstellt.

→  


Farbpolarisation und Farbladung

 		ausblenden

In Arbeit …

←   Quantenchromodynamik (Hadronen-Modell)

▾ Notizen

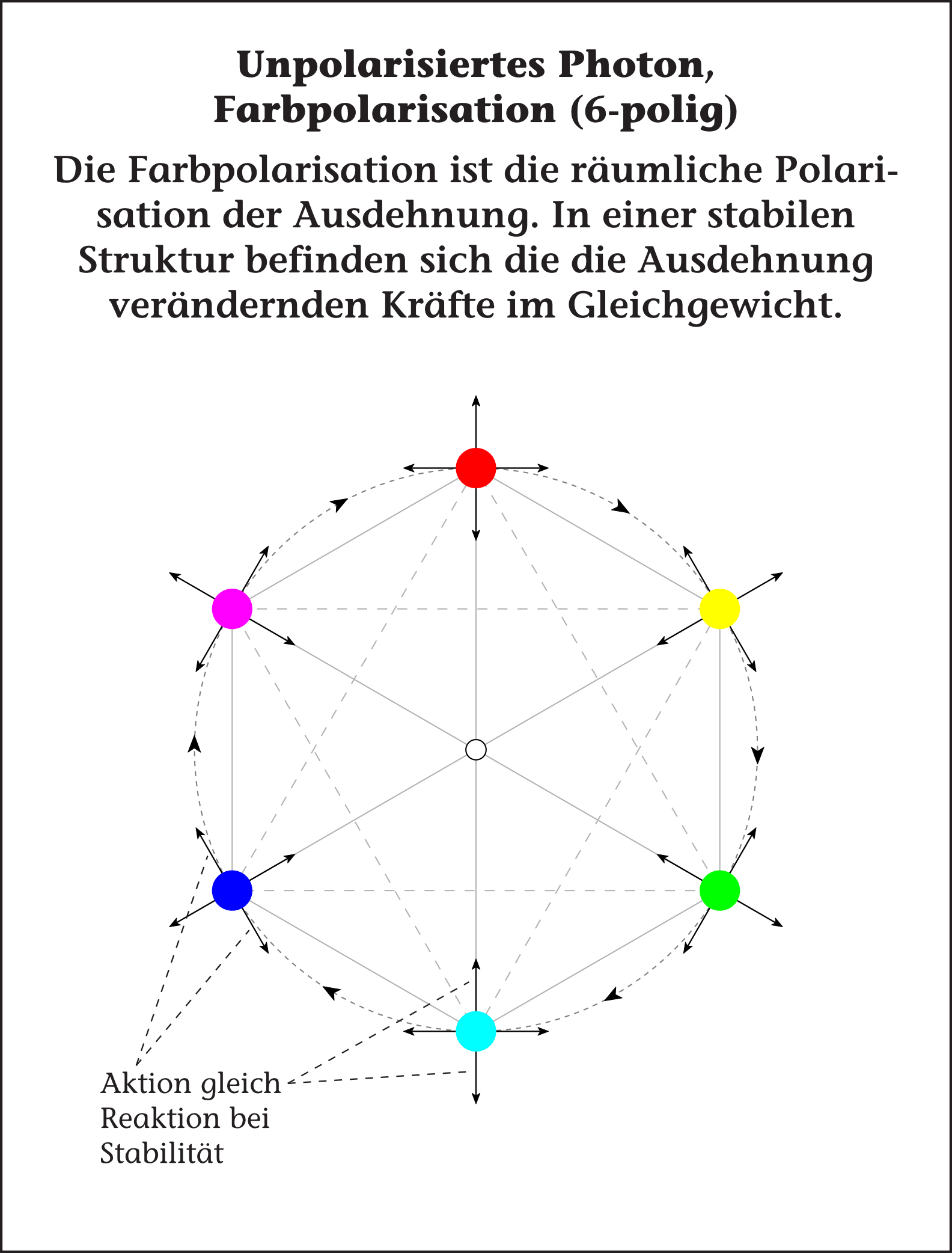
• Da die Farbpolarisation, die der Farbladung zu grunde liegt, von der Raumrichtung abhängig ist, ist ihr je Richtung eine von drei Farben zugewiesen. Diese Farben sind rot, grün und blau sowie in der jeweils entgegengesetzten Richtung antirot, antigrün und antiblau. Die Farbpolarisation entsteht durch die Symmetriebrechung der grundlegenden Zeitbewegung der Wirkungsquanten.
• Am Photon kann man erkennen, wie die Quantität der Farbpolarisation zu berechnen ist. Ein Photon muss nach außen die Farbladung weiß tragen. Seine Wirkungsquanten sind aber in unterschiedlichen, nicht symmetrisch verteilten Auslenkungswinkeln und Auslenkungsabständen gebrochen. Die Summe ihrer Farbpolarisationen muss die Farbladung Null, also weiß ergeben.
• Wie Farbladung durch einen String-Versatz aus dem Rotationszentrum der Wirkungsquanten heraus funktioniert sollte das rotationspolarisierte Photon verdeutlichen, denn es trägt nach außen hin keine Farbladung. Die sich durch die variablen Abstände der einzelnen Wirkungsquanten vom Rotationszentrum ergebenden Farbladung müssen in sich ausgeglichen sein.

Vakuum-Elapson, animiert
Animation 1 New window: Ein Wirkungsquanten-String eines unpolarisierten Photons. Die Wirkungsquanten sind als rote Kugeln mit ihren abgestrahlten Impulskegeln dargestellt. Ihre Impulskegel verbinden die Wirkungsquanten zu einem geschlossenen String, der so durch einen strukturellen Regelprozess stabilisiert ist.
Ungebrochenes Wirkungsquanten
Abbildung 1 New window: (Überschrift: Ungebrochene Wirkungsquanten-Bahn? "wikelt" -> "wickelt") Ein unbebrochenes Wirkungsquant bewegt sich auf einer symmetrisch geradlinigen Bahn. Es ist nicht abgelenkt durch Wechselwirkungen.
Elapson (ep)
Abbildung 2 New window: Der kreisrunde Vakuum-Elapsonen-String ist der symmetrischste denkbare Wirkungsquanten-String. Durch einen Symmetriebruch, ausgelöst durch ihre Wechselwirkung innerhalb des Strings, sind die sich eigentlich gradlinig bewegenden Wirkungsquanten auf eine Helixspiralbahn ausgelenkt. Sie laufen nun auf dem tiefsten Ring des Sombrero-Potentials eines Felds, dass dem Higgs-Feld sehr ähnelt. Jedes Wirkungsquant erhält so einen Spin und eine Farbpolarisation, die von der Richtung und dem Abstand seiner Auslenkung abhängt. Weil die Auslenkungen aller Wirkungsquanten des Strings sich in jeder Richtung ausgleichen, trägt der String nach außen hin die neutrale Farbladung weiß. In der Realität sind extrem viele, sehr kleine Wirkungsquanten im String, die sehr nahe beieinander liegen.
Unpolarisiertes Photon, Farbpolarisation (6-polig)
Abbildung 3 New window: Das Kräftegleichgewicht der einfachsten räumlichen Struktur entspricht dem Krempenring eines Sombrero-Potentials. Der Symmetriebruch der die räumliche Struktur gebenden Auslenkung der Bewegung der Wirkungsquanten aus der Mitte auf den Ring wird hier symbolisch mit einer Farbpolarisation in der Ebene dargestellt. Die reinste und intensivste Farbe stellt den optimalen Abstand dar, in Bezug zu seiner Rotationsfrequenz. Zur Mitte hin werden die Farben unpolarisiert und neutral weiß. Nach außen gehen sie ins Graue bis hin zum Schwarz. Drei Grundfarben mit Komplementärfarben sind notwendig, dies in der Ebene zu veranschaulichen. Diese Struktur entspricht interessanterweise genau einem der vier sechseckigen Schnitte durch einen Kuboktaeder des Vektor-Gleichgewichts. Durch ihre Rotation wechseln die Wirkungsquanten ihre Farbpolarisation ständig.

Farbpolarisation

Die Farbpolarisation eines Wirkungsquants entsteht durch seine Auslenkung von seiner geradlinigen Bewegungsmitte, auf der es sich bewegen würde, wenn es nicht in einem String eingebunden wäre. Die Wechselwirkung mit den anderen Wirkungsquanten des Strings zwingt seine Bewegung aber auf eine Helixspiralbahn.

Die Farbpolarisation eines Wirkungsquants berechnet sich aus dem Auslenkungsvektor, also dem Auslenkungswinkel und dem Auslenkungsabstand.

Die Rotationsrichtung spielt dabei keine Rolle, sie steckt im Spin des Teilchens.

Die Charakteristik sieht so aus: XXX XXX XXX XXX XXX XXX XXX

•

Die Farbe wird demnach durch die Richtung der Auslenkung bestimmt (Farbton, Hue).

•

Eine unausgelenkte Position würde mit weiß dargestellt.

•

Ein Auslenkungsradius, der der Rotationsfrequenz entspricht, ist maximal bunt und gesättigt (Sättigung).

•

Weiter innen wird es weißer und weiter außen schwärzer (Leuchtkraft, Luminance).

•

Jeweils gegenüber liegen sich Komplementärfarben.

•

Weiß bedeutet hier in einem Zusammenhang stehend, existent, auf einen Ort oder Punkt bezogen, neutral in sich abgeschlossen.

•

Schwarz bedeutet ohne Zusammenhang, also nicht existent, offen.

•

XXX

Jede Richtung im dreidimensionalen Raum sollte so eine einzigartige Farbe haben. Unsere bekannten Farben, rot, grün und blau (RGB), reichen, nach den obigen Bedingungen, allerdings nur für die Richtungen einer Ebene. Für die dritte Dimension wird noch eine vierte Farbe mit Komplementärfarbe benötigt, die vielleicht auch durch ein geeignetes Muster dargestellt werden könnte.

XXX Mehr zur Farbpolarisation im Abschnitt Definition von Subräumen. XXX XXX XXX

Farbladung

Die Farbladung ist, wie oben beschrieben, die Summe aller Farbpolarisationen der Wirkungsquanten eines Wirkungsquanten-Strings oder eines bestimmten Teils des Strings. Jeder Wirkungsquanten-String in der Quanten-Fluss-Theorie ist in seiner Summe weiß.

Anders sieht dies für Teil-Strings aus: Die Quarks eines Hadrons sind solche Teil-Strings in Form von Ecken (⅓ eines Leptonen-Strings) und Schlaufen (⅔ eines Leptonen-Strings) entsprechen. Diese Teil-Strings tragen für sich genommen eine Farbladung als Summe, die nicht weiß ist. Erst alle zusammen ergeben weiß.

Da sich die Ecken und Schlaufen in einer Ebene befinden, reichen in diesem Fall drei Farben aus, um die Ladungsverteilung zu beschreiben. Daher kommt die Quantenchromodynamik mit den RGB-Farben aus, denn es interessiert nur die relative Ladungsverteilung innerhalb eines Strings. XXX XXX XXX XXX In Arbeit … XXX

Die Farbladung eines Wirkungsquanten-Strings, oder von einem seiner Abschnitte, ist die Summe der Auslenkungsvektoren seiner Wirkungsquanten. Beim Aufsummieren ist zu beachten, dass die Auslenkungsvektoren nicht vom selben Ursprung ausgehen, sondern nebeneinander senkrecht auf der Lichtbahn des Strings stehen. Auch muss die Zeiverzögerung berücksichtigt werden, mit der die Wechselwirkung auf andere Abschnitte des Strings wirkt. Dabei ist wiederum zu berücksichtigen mit welcher Geschwindigkeit sich die Wechselwirkung ausbreitet, mit Lichtgeschwindigkeit oder mit erhöhter Lichtgeschwindigkeit(Link). Auch ist die Frage, welcher Anteil entlang des Strings läuft und welcher quer durch den Raum geht, falls dies zu unterscheiden ist. Oder ist die String-Spannung völlig unabhängig von der Farbladung? Wie die Summe genau zu bilden ist muss noch untersucht werden.

Vakuum, Vektor-Gleichgewicht und Farbpolarisation

» The vector equilibrium is the zero starting point for happenings or nonhappenings: it is the empty theater and empty circus and empty Universe ready to accommodate any act and any audience. « ~Richard Buckminster Fuller

Das Vakuum, welches aus unpolarisierten Photonen, aus Vakuum-Elapsonen, besteht, muss sich in einem dreidimensionalen, räumlichen Kräftegleichgewicht befinden. Nach Richard Buckminster Fuller ist dies das Vektor-Gleichgewicht in Form eines Kuboktaeders.

Die kleinste Menge an Grundfarben in einer Ebene, um eine Struktur erhaltende Ausdehnungspolarisation darzustellen, sind drei, wenn sich die Farben auf dem sich ergebenden Ring nicht wiederholen sollen (siehe ). Inklusive ihrer Komplementärfarben ergeben sich so sechs Farben, die auf einem Ring ein Sechseck abbilden. Diese Struktur entspricht interessanterweise genau einem der vier sechseckigen Schnitte durch einen Kuboktaeder des Vektor-Gleichgewichts.

Auch andere, wie Nassim Haramein, haben erkannt, dass damit die isotrope Vektor-Matrix der Stabilität des Vakuums zugrunde liegt. Dieser Zusammenhang mit der Farbpolarisation und darüber mit der Grundstruktur der Elementarteilchen-Strings der Quanten-Fluss-Theorie unterstricht diese Sichtweise und begründet sie noch tiefgehender durch beobachtete Eigenschaften der Quantenchromodynamik.

XXX XXX XXX XXX In Arbeit … XXX

Regelprozesse und das Sombrero-Potential des Higgs-Mechanismus

Einfache Regelprozesse, die eine Struktur in einer bestimmten Ausdehnung stabilisieren, laufen in einem Potential von Spieler und Gegenspieler, das die Form einer Sombrero-Hutkrempe hat (siehe (Animation einfügen!)). Im Higgs-Mechanismus oder Higgs-Feld spielt ein solches Sombrero-Potential eine zentrale Rolle.

Ich nehme stark an, dass an dieser Stelle das Verständnis von Elementarteilchen als strukturelle Regelprozesse Brücken zwischen der Gravitation, der Masse eines Elementarteilchens, der elektroschwachen Wechselwirkung, der Quantenchromodynamik und der Ausdehnung eines Elementarteilchens schlägt. Dies wird sich in der Quanten-Fluss-Theorie im Laufe der Zeit immer weiter herauskristallisieren. XXX XXX XXX XXX XXX XXX XXX XXX XXX In Arbeit … XXX

XXX

XXX XXX XXX XXX XXX XXX XXX XXX XXX In Arbeit … XXX

→  

ausblenden

Quarks

 		ausblenden

Protonen, Neutronen und Mesonen

←  

▾ Notizen

• Besitzen u- und d-Quarks unterschiedliche Frequenzen, weil sie verschiedene Massen haben?
– Wenn ja, dann rotieren ihre Wirkungsquanten unterschiedlich schnell um die Lichtbahn. Es ist im Hadron ja ein riesen Chaos von virtuellen Quarks und Gluonen. Vielleicht zerreißt der String ihres Hadrons dann ständig?
– Wenn nein, wie kommt dann die gleiche Frequenz zustande? Bewegen sich die leichteren Quarks im Raum dann schneller und kommen so auf die gleiche Frequenz? Oder sind sie durch den gemeinsamen String ihres Hadrons zwangssynchronisiert? Was genau erzeugt ihren Wirkungsquanten-Rotationsradius? Durch die Störungswellen der Wirkungsquanten des Strings selber? Der Mechanismus muss sich ja irgendwie von dem der Elapsonen bzw. Photonen unterscheiden! Den bei den Elapsonen kann keine Wechselwirkung von der gegenüberliegenden Seite des Strings ausgehen. Es können sich nur die benachbarten Wirkungsquanten beeinflussen. Mit anderen Worten: Wie funktioniert die WW der Farbpolarisation?
– Unterschied: Die Elapsonen haben ihre WW nur innerhalb ihres Strings, denn ein WQ kann nur das oder die benachbarten WQs beeinflussen. Bei den Leptonen und Hadronen ist dies anders: Weil diese sich nicht mit LG bewegen kann die Farbpolarisation und die elektroschwache Polarisation auf alle anderen Teile des Strings wirken.
• Quarks sind ein Drittel- oder Zweidrittelausschnitte aus Leptonen. Je kleiner der Ausschnitt, desto größer die Farbladung? Das kann eigentlich nicht sein. Denn die beiden Hälften eines Leptons müssen eine entgegengesetzte Farbladung des gleichen Betrags tragen; zueinander die jeweilige Antifarbladung. Soll die Farbladung eines Leptons nach außen hin neutral weiß sein, so muss jedes Teilstück eines Leptonen-Strings die Antifarbladung zum Rest des Strings tragen.

In Arbeit … XXX XXX XXX XXX XXX XXX XXX XXX XXX

XXX - XXX
Abbildung 4 New window: XXX XXX XXX

Protonen und Neutronen

Die Hypothese, dass Down-Quarks elektrisch negativ geladene ⅓-Leptonen und Up-Quarks elektrisch positiv geladene ⅔-Leptonen sind, passt so erst einmal gut zu den Werten, die sich für die Ladung der Protonen und Neutronen ergeben:

\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { | \MUp{}\MRi{p}^{+1} \rangle\;\;\;=\;\;\;| \PuUp \rangle + | \PuUp \rangle + | \PdDown \rangle } \] (QCD.Q.1)
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm} q_{p}\;\;\;=\;\;\;1 e\;\;\;=\;\;\;\frac{2}{3} e + \frac{2}{3} e - \frac{1}{3} e } \] (QCD.Q.2)
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { | \MDo{}\MLe{n}^{\,0} \rangle\;\;\;=\;\;\;| \PuUp \rangle + | \PdDown \rangle + | \PdDown \rangle } \] (QCD.Q.3)
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm} q_{n}\;\;\;=\;\;\;0 e\;\;\;=\;\;\;\frac{2}{3} e - \frac{1}{3} e - \frac{1}{3} e } \] (QCD.Q.4)

Abweichung vom Quark als anteiliges Lepton beim Spin
Eine Abweichung vom anteiligen Lepton stellt der Spin dar, der sowohl für das Proton und Neutron als auch für die Quarks mit \( \pm ½ \hbar \) halbwertig ist:

\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { s_{p}\;\;\;=\;\;\;\frac{1}{2} \hbar\;\;\;=\;\;\;\frac{1}{2} \hbar + \frac{1}{2} \hbar - \frac{1}{2} \hbar } \] (QCD.Q.5)
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { s_{n}\;\;\;=\;\;\;-\frac{1}{2} \hbar\;\;\;=\;\;\;\frac{1}{2} \hbar - \frac{1}{2} \hbar - \frac{1}{2} \hbar } \] (QCD.Q.6)

Quark und Leptonen Umwandlungen
In der Natur zerfallen Neutronen nach einer bestimmten Halbwertszeit jeweils in ein Proton, ein Elektron und ein Elektron-Anti-Neutrino, wobei noch Photonen entstehen können:,

\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \MDo{}\MLe{n}^{\,0}\;\;\;\rightarrow\;\;\;\MUp{}\MRi{p}^{+1} + \MDoDo{}\overset{\leftleftarrows}{W}^{\raise -1.2ex {-1}} + \MUpDo{}\gamma \\ \qquad\, \rightarrow \;\;\; \MUp{}\MRi{p}^{+1} + \MDo{}\MLe{e}^{-1} + \MDo{}\MLe{\overline{\nu}}_{e}^{\raise -.9ex {\,0}} + \MUpDo{}\gamma } \] (QCD.Q.7)

Die durch die Pfeile dargestellte und mit dem Leptonen-Modell zusammenhängende Spin-Symbolik erkläre ich im Abschnitt Symbolismus der Seite Elektroschwache Wechselwirkung.

Im Grunde setzt hierbei die Umwandlung eines Down-Quarks des Neutrons in ein Up-Quark des dadurch entstehenden Protons ein W-1 Boson der schwachen Wechselwirkung frei, das dann in ein Elektron und ein Elektron-Anti-Neutrino zerfällt:

\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \PdDown\;\;\;\rightarrow\;\;\;\PuUp + \MDoDo{}\overset{\leftleftarrows}{W}^{\raise -1.2ex {-1}} + \MUpDo{}\gamma } \] (QCD.Q.8)
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \MDoDo{}\overset{\leftleftarrows}{W}^{\raise -1.2ex {-1}}\;\;\;\rightarrow\;\;\;\MDo{}\MLe{e}^{-1} + \MDo{}\MLe{\overline{\nu}}_{e}^{\raise -.9ex {\,0}} } \] (QCD.Q.9)

Ladungserhaltung verletzender Neutronen-Zerfall
In Arbeit … Lässt sich dieser ungewöhnliche Zerfall mit dem neuen Elementarteilchen-Modell erklären? Wie erklärt das Standardmodell der Teilchenphysik ihn? XXX XXX XXX XXX XXX:

\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \MDo{}\MLe{n}^{\,0}\;\;\;\rightarrow\;\;\;\MUp{}\MRi{p}^{+1} + \MDo{}\MLe{\nu}_{e}^{\raise -.9ex {\,0}} + \MDo{}\MLe{\overline{\nu}}_{e}^{\raise -.9ex {\,0}} } \] (QCD.Q.10)

XXX
XXX XXX XXX XXX XXX XXX In Arbeit … XXX

Farbladung

XXX XXX XXX XXX XXX XXX XXX XXX XXX In Arbeit … XXX

Mesonen

XXX XXX XXX XXX XXX XXX XXX XXX XXX In Arbeit … XXX

XXX

XXX XXX XXX XXX XXX XXX XXX XXX XXX In Arbeit … XXX

→  

ausblenden

Gluonen

 		ausblenden

In Arbeit …

←  

(• Im Gegensatz zu Elapsonen gibt es eine WW zwischen Gluonen, die auch in der FrQFT ersichtlich ist, da Gluonen String-Ausschnitte der Elapsonen sind. Gucken, ob sich hierzu etwas in Ent, »Der Klebstoff der Welt«, findet. Sonst im Artikel auf Spektrum.de, Dirk Eidemüller, Ein Teilchen aus elementarer Kraft?, URL: http://www.spektrum.de/news/ein-teilchen-aus-elementarer-kraft/1372085)

In Arbeit … XXX XXX XXX XXX XXX XXX XXX XXX XXX

→  

ausblenden

Confinement

 		ausblenden

In Arbeit …

←  

(• Dieser Ansatz ist etwas sehr besonderes! Siehe auch SdW 12/2013 Preonen-Artikel. S. 50-51.)

Mit dem Confinement ist das Eingesperrtsein der Quarks und Gluonen in allen Hadronen, wie den Protonen und Neutronen des Atomkerns, gemeint. Man kann ein Quark nicht einfach aus einem Proton herausziehen. Sein Widerstand gegen das Herausziehen und der Energieaufwand wächst sogar erheblich an, umso weiter man es schon aus dem Proton herausbewegt hat.

Doch wenn Quarks, wie oben beschrieben, alle gemeinsam Teil des geschlossenen Strings eines Hadrons sind, dann leuchtet es sofort ein, dass man sie nicht ohne weiteres aus diesem Wirkungsquanten-String lösen kann. Denn in der Quanten-Fluss-Theorie gibt es nur geschlossene Wirkungsquanten-Strings. Um ein Quark heraus zu ziehen muss der String länger werden. Das bedeutet, er muss mit Wirkungsquanten aufgefüllt werden. Wirkunsgquanten sind Energieeinheiten, die in diesem Fall massiv zugeführt werden müssen. Führe ich so viele Wirkungsquanten hinzu, dass der String reißt, so bilden sich aus den nun reichlich vorhandenen Wirkungsquanten neue geschlossene Strings und somit auch Quanrks und Gluonen, so dass am Ende ein neues Hadron-Antihadron-Paar mit dem herausgezogenen Quanrk entsteht. Auch der Platz im ursprünglichen Proton wird wieder durch ein neues Quark ersetzt.

Das Confinement der Quarks und Gluonen ist also eine logische Schlussfolgerung des Hadronen-Modells in der Quanten-Fluss-Theorie. Die Quantenchromodynamik wird so um detailierte Bilder von den Hintergründen und Ursachen ergänzt, die eine tiefere Einsicht in die Zusammenhänge ermöglichen.

→   Quantengravitation der Elementarteilchen

ausblenden

Fußnoten

 		ausblenden
1. (Primärliteratur einfügen!)
Sekundärliteratur:
Vgl. Ent, »Der Klebstoff der Welt«.
Internet:
Vgl. Wikipedia, Quantenchromodynamik.
2. (Primärliteratur einfügen!)
Internet:
Vgl. Wikipedia, Higgs-Mechanismus, Higgs-Potential (mit Veranschaulichung).
Vgl. Müller, Higgs-Teilchen, Symmetriebrechung anschaulich.
3. (Primärliteratur einfügen!)
Sekundärliteratur:
Vgl. Ent, »Der Klebstoff der Welt«, S. 60, 61.
Internet:
Vgl. Wikipedia, Confinement.
Vgl. Alkofer, Quark Confinement (Online), S. 1.
4. Buckminster Fuller, Richard, SYNERGETICS (2nd. Ed.) at Sec. 503.03; 11 Dec'75.
Internet:
Cosmometry, Vector Equilibrium & Isotropic Vector Matrix. URL: https://cosmometry.net/vector-equilibrium-&-isotropic-vector-matrix.
5. Vgl. Beringer, Particle Physics Booklet, S. 8-9, 144-145.
Vgl. Fritzsch, Mikrokosmos, 6. Kap. Elektroschwache Wechselwirkungen, S. 105-118, hier S. 106.
Internet:
Vgl. Wikipedia, Weak interaction, Interaction types, Charged current interaction.
Spin und elektrische Ladung des W±-Bosons vgl. Wikipedia, W-Boson.
Schwacher Isospin und schwache Ladung des W±-Bosons vgl. Wikipedia, Schwache Ladung, Kopplungen der elektroschwachen WW im Standardmodell.
6. Dazu hab ich probeweise Auflistungen in meinem unveröffentlichten Manuskript v8.009 vom 18.07.2015.
7. Vgl. Beringer, Particle Physics Booklet, S. 144-145, hier S. 145.
8. (Primärliteratur einfügen!)
Sekundärliteratur:
Vgl. Ent, »Der Klebstoff der Welt«, S. 60, 61.
Internet:
Vgl. Wikipedia, Confinement.
Vgl. Alkofer, Quark Confinement (Online), S. 1.
ausblenden

Stand 21. Mai 2021, 09:00 CET.


Permanente Links:
(Klicke auf die Archivlogos
zum Abruf und Ansehen
der Archive dieser Seite.)

Logo Wayback Machine
archive.today
webpage capture