| ← |
Raum, Zeit, Alterung, Frequenz und Energie
Das strukturelle und prozessuale Verständnis von Raum und Zeit im Pound-Rebka-Snider-Experiment – die formale Lösung des ›Problems der Zeit‹
Zur Lösung des ›Problems der Zeit‹ wird in der Quanten-Fluss-Theorie zwischen drei verschiedenen Arten von Zeit unterschieden. Diese Zeitarten existieren in der Physik danach gemeinsam. Dies ist zum einen die räumlich absolut erscheinende der relativistischen Quantenfeldtheorie, als zunächst absolut . Zum zweiten sind es die Schwingungen der relativistischen Quantenfeldtheorie. Und zum dritten ist dies die , deren Veränderungen den aus der Allgemeinen Relativitätstheorie bekannten, räumlich variablen Alterungsprozessen zugrunde liegt. Dabei ist die Alterung die prozessuale Veränderung an einem Ort im Raum, die der Bewegung des Lichts im dreidimensionalen, entspricht. Die Lichtgeschwindigkeit sowie der strukturierte Raum im Gravitationsfeld sind nur an Orten des Kosmos in jeder Raumrichtung gleich – also isotrop. Im Allgemeinen variieren diese Eigenschaften an einem bestimmten Ort im Bewegungsraum je nach Raumrichtung.
Die variable Lichtgeschwindigkeit im dreidimensionalen Raum und der variabel strukturierte Raum spiegeln in der Quanten-Fluss-Theorie die Raumzeitkrümmung der Allgemeinen Relativitätstheorie wider. Damit handelt es sich in der neuen Theorie bei diesem Phänomen um reale Strukturveränderungen des Vakuums und der Elementarteilchen im an sich . Dies bedeutet, dass der Eindruck der Raumzeitkrümmung durch eine variable Dichteverteilung und durch variable Bewegungsmuster der Feinstruktur des Vakuums und der Elementarteilchen hervorgerufen wird. Diese Feinstruktur wird in der Quanten-Fluss-Theorie durch sogennate Wirkungsquanten gebildet. Die folgenden Kapitel beschäftigen sich mit der Entwicklung der mathematischen Beschreibung der Bewegungsstruktur eines lichtähnlichen Teilchens – hier allgemein Elapson (ep) genannt, quasi der Prototyp eines Photons (ph) – und der Wirkungsquanten (wq) des Vakuums.
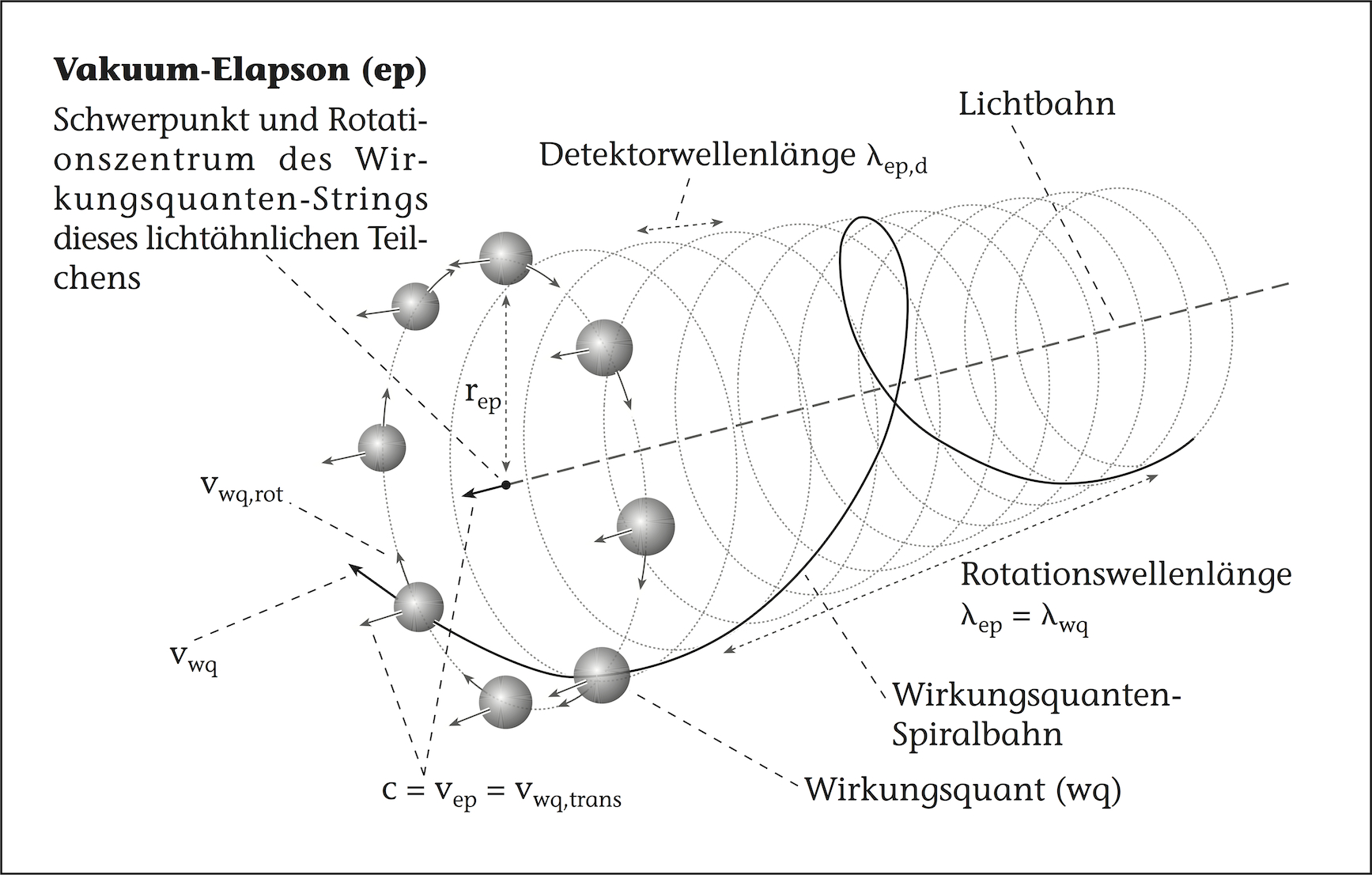
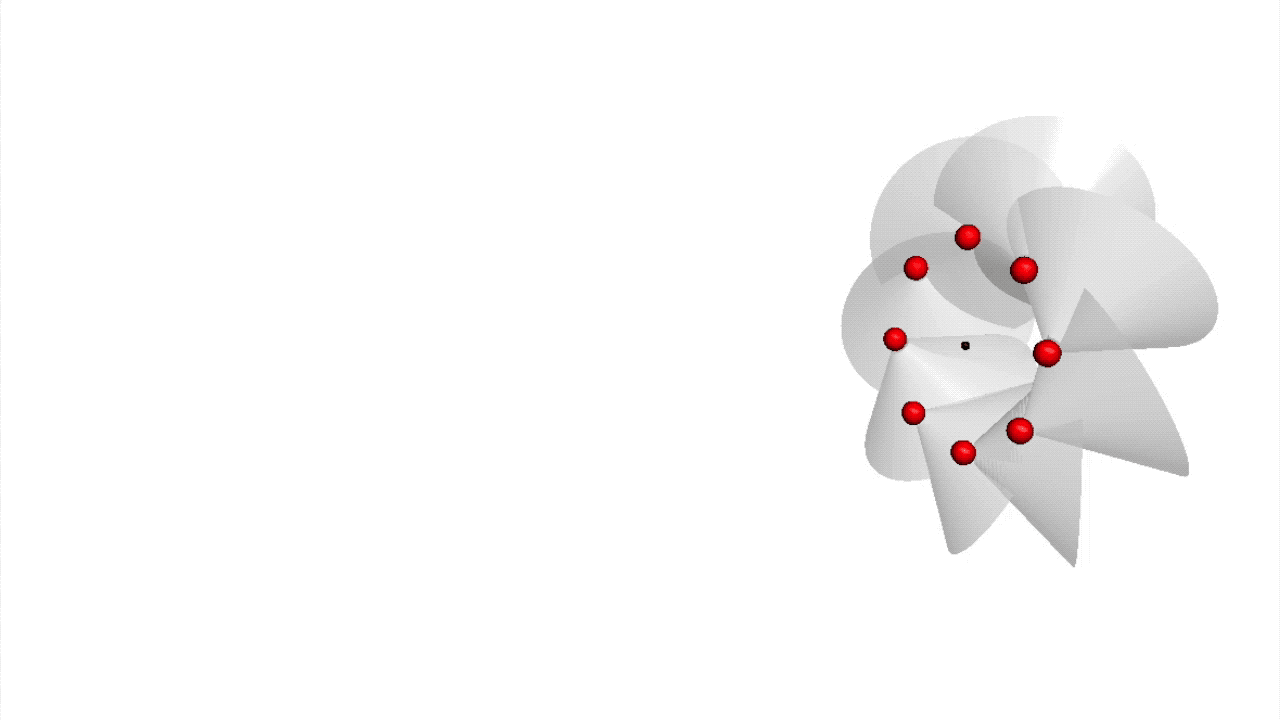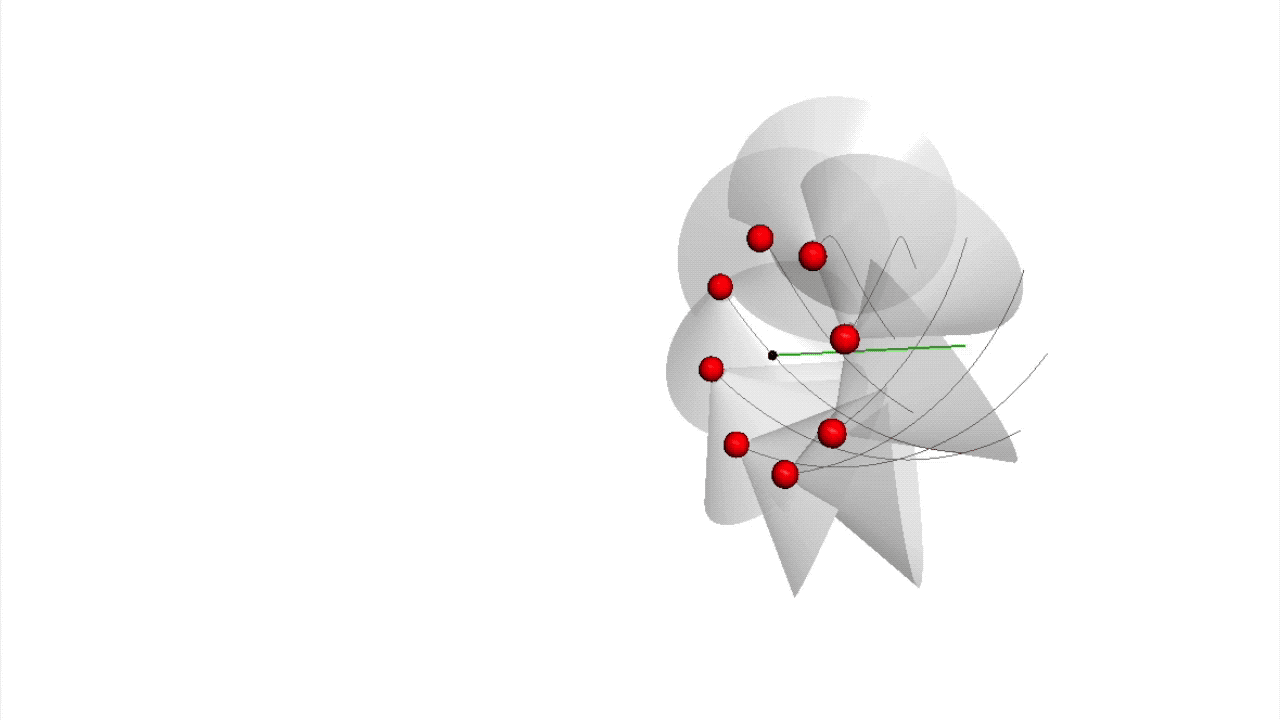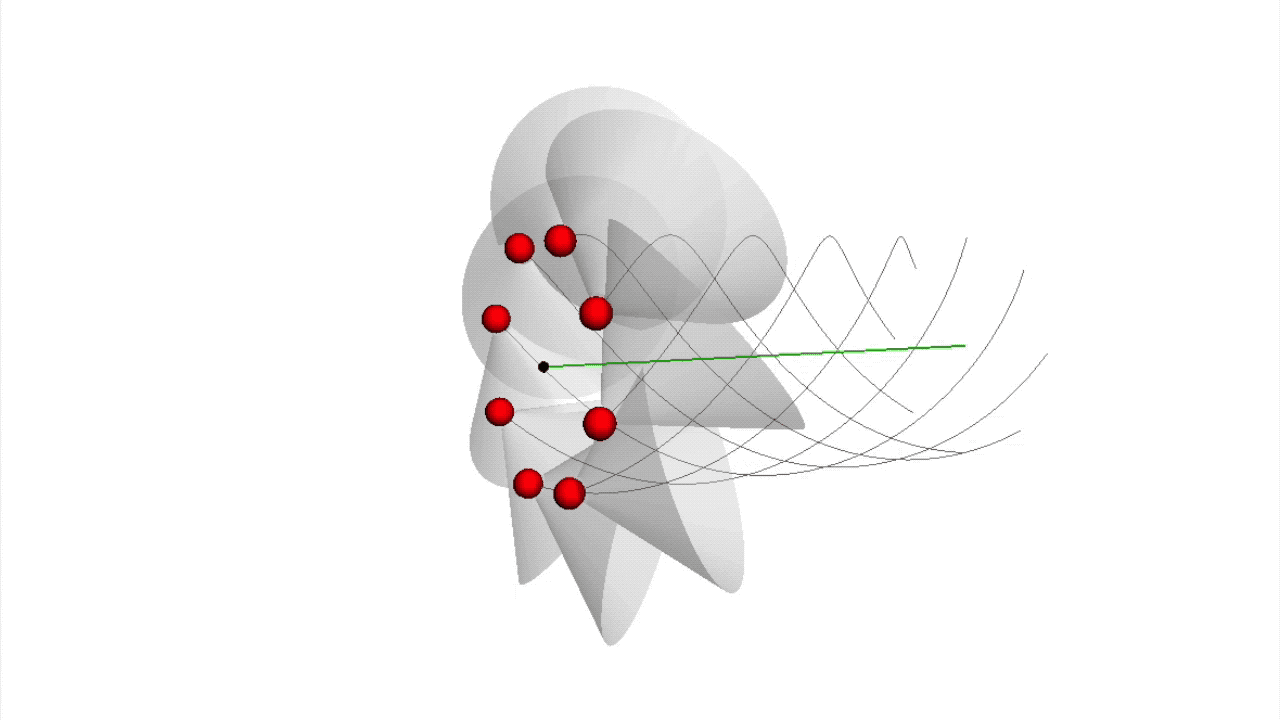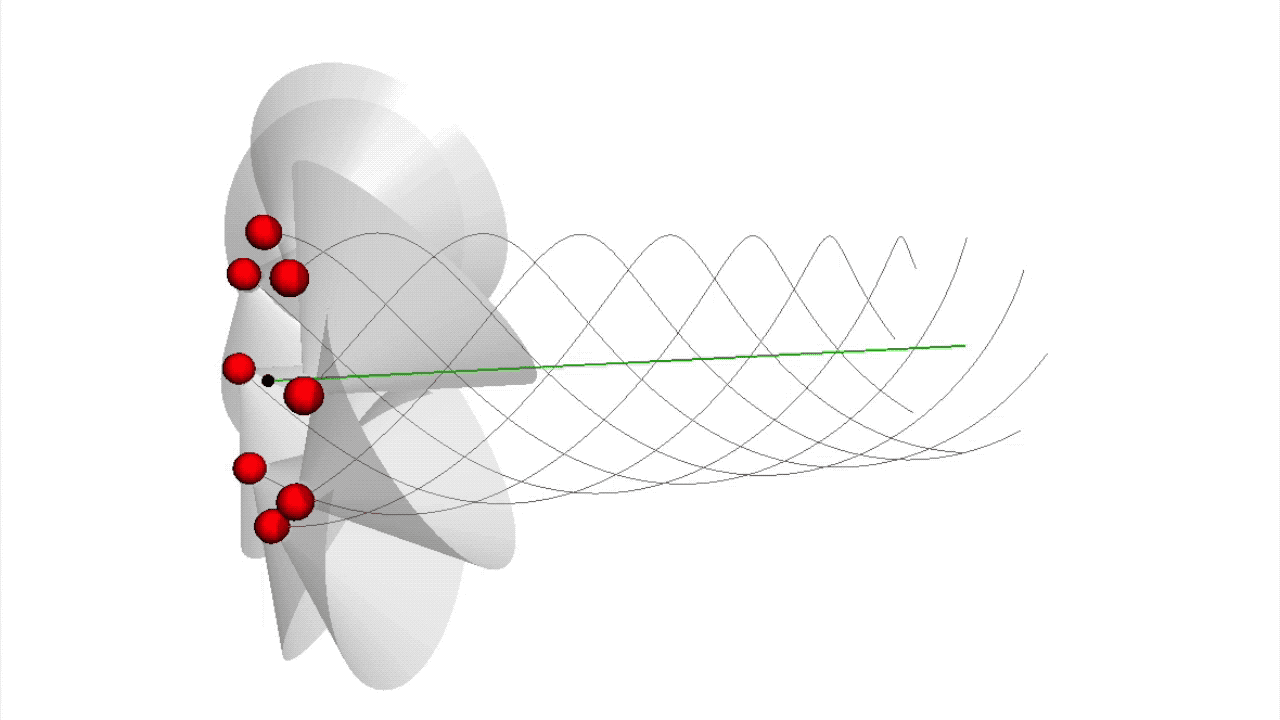
Beschäftigt man sich mit dem Zusammenhang zwischen der Alterung sowie der inneren Frequenz eines Elementarteilchens und versucht diesen durch verschiedene Bewegungen zu beschreiben, so macht man eine erstaunliche Entdeckung: Es kommt eine grundlegende Zeit in Form der zum Vorschein. Diese ist grundlegender als die Bewegung des Lichts. Die Wirkungsquanten bewegen sich mit √2⋅c0 auf einer helixförmigen Spiralbahn (siehe ), und dies unabhängig von der wirkenden Gravitation. c0 steht dabei für die Lichtgeschwindigkeitskonstante. Ihre Rotationsbewegung entspricht der inneren Frequenz des Vakuums und seiner Elementarteilchen und ihr Vorwärtsschrauben – ihre Translation – entspricht der örtlichen, je nach Gravitation und Richtung variablen Lichtgeschwindigkeit im dreidimensionalen Raum, wie sie aus der Allgemeinen Relativitätstheorie bekannt ist.
|
Der hier eingeführte Zusammenhang zwischen drei Bewegungskomponenten von Raum und Zeit als unterschiedliche zeitliche Aspekte der Physik, ist der erste Schritt zur Entwicklung der fraktalen Struktur der Quanten-Fluss-Theorie. Diese fraktale Struktur ermöglicht anschließend ein tiefgehendes Verständnis der Quantengravitation einschließlich des Phänomens der Dunklen Materie. Auch erschließt sich das Innenleben Schwarzer Löcher und der Aufbau des Universums.
| → |
|
Einführung |
|
Konzept des Kosmos, seiner Beobachtung und seiner Erhaltungssätze
| ← |
(• Die Konstanz der Wirkungsquanten-Geschwindigkeit ergibt sich nur im euklidischen Wirkungsquanten-Bewegungsraum! Die Konstanz der LG gilt nur im gekrümmten Licht-Bewegungsraum.)
Erhaltungssätze des Bewegungsraums des Kosmos und deren Brüche
In der Quanten-Fluss-Theorie ist der Raum des Kosmos mit Wirkungsquanten und den von ihnen gebildeten Wirkungsquanten-Strings der Elementarteilchen gefüllt. Im Kosmos gilt dabei eine erweiterte Energieerhaltung. Zum einen ist es die bekannte Energieerhaltung. Weil Wirkungsquanten Energieeinheiten sind, kann sich deren Anzahl im Kosmos unter normalen Umständen nicht verändern. Nicht einmal beim Übergang in ein Schwarzes Loch.
Aus der fraktalen Struktur des Universums ergibt sich auf gleiche Weise die Anzahlerhaltung der Elementarteilchen-Strings. Zu ihnen zählen auch die Vakuum-Elapsonen-Strings, die überdeutlich in der Mehrheit sind und deshalb bei der gleich folgenden im Vordergrund stehen. Die Elementarteilchen-String-Anzahlerhaltung gilt nur nicht beim Übergang in ein Schwarzes Loch. Dieser Bruch der Elementarteilchen-String-Anzahlerhaltung spielt allerdings nur bei der Betrachtung der in Bezug auf die Feststellung der Existenz Schwarzer Löcher eine Rolle. Bei der Betrachtung der Gravitation im Kosmos findet der Bruch der Elementarteilchen-String-Anzahlerhaltung keine weitere Beachtung.
Weil die Wirkungsquanten nicht nur Energieeinheiten, sondern ebenso Impuls- und Masseneinheiten sind, gilt auch Impuls-, Drehimpuls- und Massenerhaltung.
|
|
Euklidisch flacher Kosmos mit lokalem Symmetriebruch
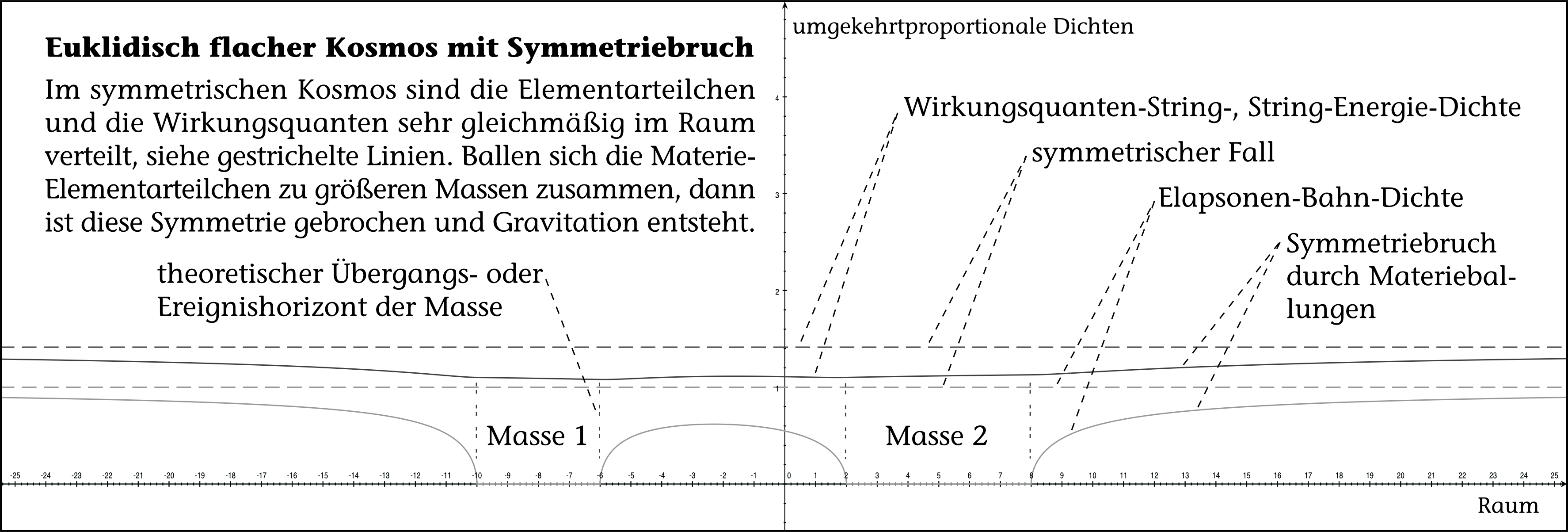
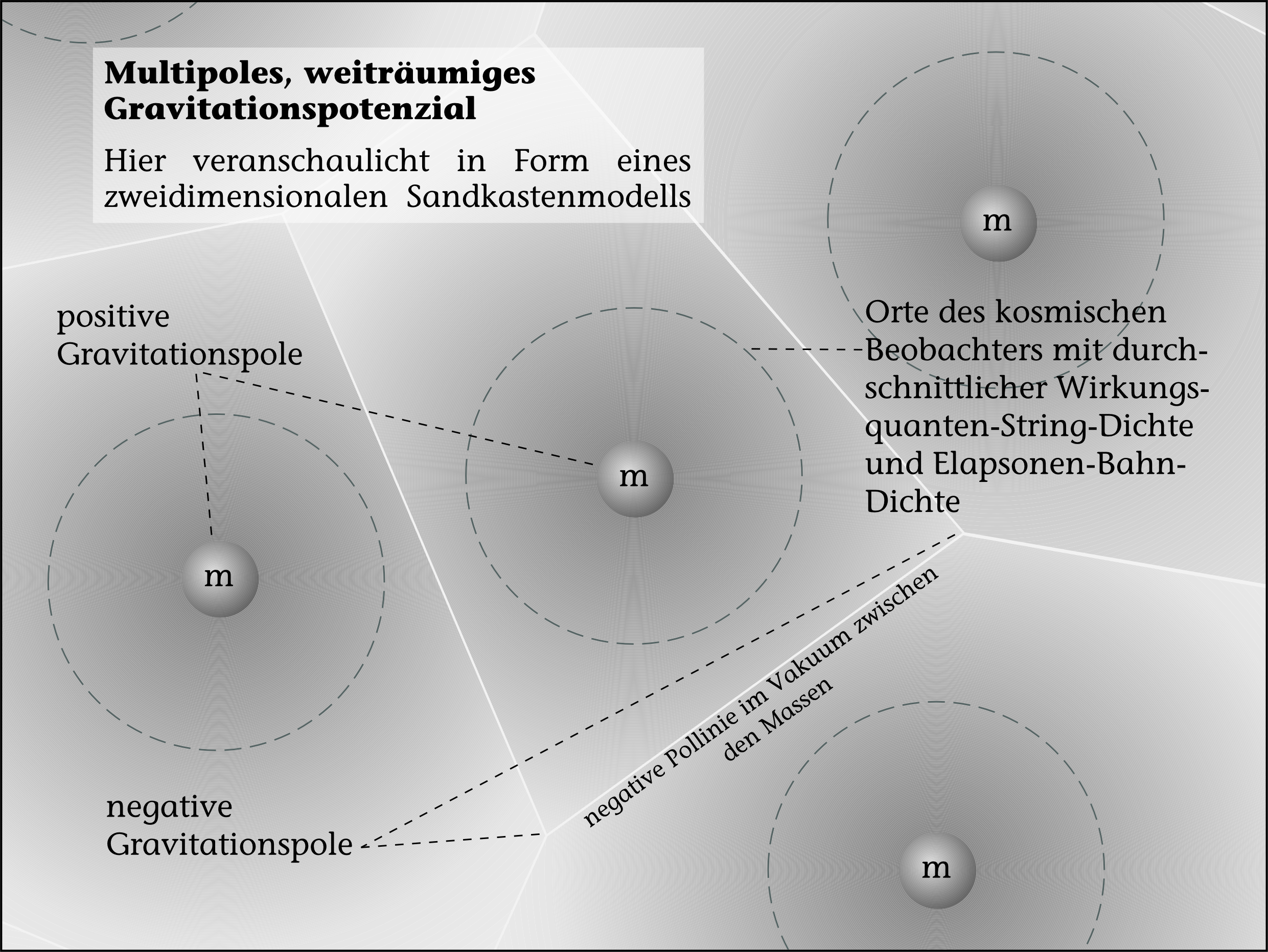
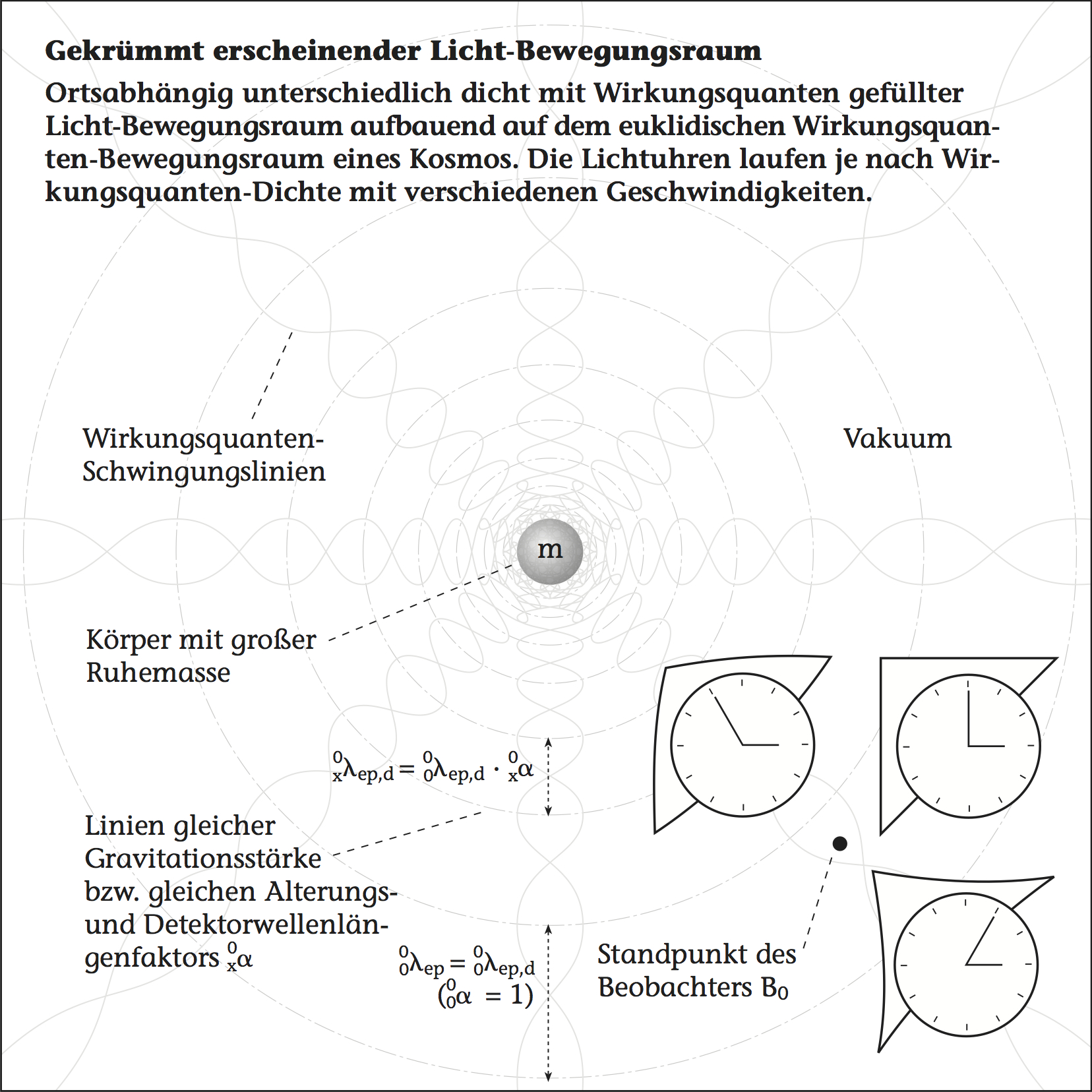
Das der Kosmos aus der körnigen Struktur der Wirkungsquanten besteht, hat Konsequenzen. Es existiert ein symmetrischer Zustand des Raums im Kosmos: Ähnlich wie in einem Sandkasten ist dann die Symmetrie hergestellt, wenn alle Wirkungsquanten gleichmäßig im Kosmos verteilt sind (siehe , dunkle gestrichelte Linie). Gleiches gilt für die Elementarteilchen-Strings (, helle gestrichelte Linie). Dieser theoretische Zustand wäre der symmetrische und euklidisch flache Kosmos. Wird diese Symmetrie gebrochen und gerät außer Balance, so entsteht die lokal asymmetrische Gravitation, die wir in unserem Kosmos beobachten (siehe , durchgezogene Linien). Die Materie-Elementarteilchen verklumpen – zu Galaxien, Sonnen und Planeten – und um sie herum erhöhen sich die relativen Dichten der Wirkungsquanten und Vakuum-Elapsonen aufs Überdurchschnittliche (siehe , negative Pole der Gravitation). Zwischen den sehr großen Massen verringert sich diese Dichte und wird unterdurchschnittlich. Im Mittel bleibt der Kosmos allerdings euklidisch Flach, genau wie es beobachtet wird.
Im Kosmos bleiben folglich Orte, an denen weiterhin eine mittlere Dichte der Wirkungsquanten und Vakuum-Elapsonen erhalten ist, wie im Druchschnitt des Kosmos. Denn auch in einem Sandkasten, in dem man den ursprünglich gleichmäßig verteilten Sand zu einem Gebirge formt, haben teile des Gebirges die gleiche Höhe, wie das ursprüngliche Niveau. Die Orte der durchschnittlichen Dichte befinden sich an den Übergangsflächen zwischen über- und unterdurchschnittlicher Dichte und umschließen die sehr großen Massen als Hüllen (siehe , gestrichelte Linien). An diesen Orten trägt die Lichtgeschwindigkeit im dreidimensinalen Raum den Wert der Lichtgeschwindigkeitskonstanten (siehe ). Und deshalb haben diese Orte des besondere Eigenschaften, wie nachfolgend beschrieben wird.
Notation
Um die Formeln der Quanten-Fluss-Theorie möglichst verständlich zu halten, selbst wenn der Sachverhalt komplexer wird, führe ich eine neue Notation ein. In dieser Notation kann sowohl der Ort des Beobachters, als auch der Ort der Beobachtung angegeben werden. Diese Angaben sind erforderlich, wenn Werte von den Eigenchaften dieser Orte abhängig sind. Zum Beispiel kann die Alterung des Beobachters ortsabhängig sein. Altert der Beobachter langsamer, so nimmt er an anderen Orten so wahr, als wenn sie schneller abliefen. Aber auch die Alterung am beobachteten Ort kann sich von Ort zu Ort unterscheiden. Wird vom Ort z aus der Ort y beobachtet, so wird dies am Beispiel der Lichtgeschwindigkeit im dreidimensionalen Raum durch folgende Notation deutlich:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {^{z}_{y}c} } \] | (ZAF.Ein.1) |
Der hochgestellte Ort z guckt auf oder beobachtet den niedrig gestellten Ort y.
Kosmische Beobachter
Um den Formalismus vom Beobachtungsstandpunkt her zu vereinfachen, kann das Geschehen aus der Sicht des Kosmos oder besser gesagt, aus der Sicht eines kosmischen Beobachters beschrieben werden. Die kosmischen Beobachter B0 an den Orten 0 zeichnet aus, dass an ihren Orten die der durchschnittlichen Dichte im Kosmos entsprechen. Zum Beispiel ist die Lichtgeschwindigkeit im dreidimensionalen Raum an seinen Orten gleich der Lichtgeschwindigkeitskonstanten (siehe , gestrichelte Linien):
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {^{0}_{0}c}\;\;\;=\;\;\;{_{\raise -.3ex 0}c}\;\;\;=\;\;\;{c_{\raise -.3ex 0}} } \] | () |
So bietet es sich an, dass beim kosmischen Beobachter die hochgestellte 0 zur Vereinfachung weggelassen werden kann. Um den Beobachtungsstandpunkt auf beliebige Beobachter zu erweitern, siehe Kapitel .
(Ist die LG auch in der ART zwischen zwei gleich großen Planeten reduziert oder nicht, wenn sich im Kosmos nur diese beiden befinden würden? Die Frage in einem Forum stellen.) Hinweis: Die Orte der kosmischen Beobachter (siehe , gestrichelte Linien) sind im asymmetrischen Fall der Wirkungsquanten-Verteilung im Kosmos (siehe , durchgezogene Linien) Orte, die immer der Gravitation ausgesetzt sind. Man unterliegt leicht dem Irrtum, dass an diesen Orten keine Gravitation wirken würde. Doch die Quanten-Fluss-Theorie unterscheidet sich an dieser Stelle leicht von der Allgemeinen Relativitätstheorie:
Bei Einstein führt jede Gravitation zur Reduzierung der Lichtgeschwindigkeit im dreidimensionalen Raum. Das bedeutet, dort wo Gravitation herrscht ist die ortsübliche Lichtgeschwindigkeit im dreidimensionalen Raum kleiner als c0. Die Orte ohne Gravitation sind die Orte, wo sich die Gravitation der größten Massenansammlungen im Kosmos aufhebt.
In der Quanten-Fluss-Theorie verhält es sich ein wenig anders: Die Anzahl der Wirkungsquanten und Elementarteilchen unterliegt jeweils der . Dabei entspricht die Elementarteilchen-Anzahl im Wesentlichen der Vakuum-Elapsonen-Anzahl, weil es von letzteren sehr viel mehr gibt. Sind die Wirkungsquanten beziehungswiese die Vakuum-Elapsonen im Kosmos auch lokal sehr gleichmäßig verteilt, so wirkt im ganzen Kosmos keine Gravitation (siehe , gestrichelte Linien). Häufen sich allerdings größere Mengen von Materie-Elementarteilchen zu großen Massen an, so ist die Dichte an Wirkungsquanten und Vakuum-Elapsonen um diese herum überdurchschnittlich (siehe , siehe durchgezogene Linien, und , innerhalb der gestrichelten Linien). An den Stellen zwischen den größten Massen des Kosmos muss die Dichte dann unterdurschnittlich sein (siehe , negative Pole der Gravitation). Die Orte der kosmischen Beobachter liegen an den zwischen über- und unterdurchschnittlicher Dichte (siehe , gestrichelte Linien). Die Gravitation hingegen hebt sich dort auf, wo Dichteminima sind, bei den negativen Polen der Gravitation. Das heißt, genau wie bei Einstein, an den Orten wo sich die Gravitation der größten Massenansammlungen im Kosmos aufhebt.
Der Unterschied zwischen beiden Theorien ist zunächst marginal: Zwischen den größten Massenansammlungen im Kosmos ist unglaublich viel Volumen. Aus Sicht der Quanten-Fluss-Theorie ist die Dichte an den Orten der negativen Pole der Gravitation also nur sehr leicht unterdurchschnittlich. Die ortsübliche Lichtgeschwindigkeit im dreidimensionalen Raum ist folglich nach Formel dort auch nur sehr leicht über der Lichtgeschwindigkeitskonstanten, was wir als Beobachter von der Erde aus kaum bemerken können. Denn dort befindet sich ja fast keine Materie. Allerdings entfaltet dieser Unterschied beim Phänomen der Dunklen Materie seine entscheidende Wirkung.
Kosmisch konstante Werte
Es gibt auch Werte, die aus einer bestimmten Perspektive nicht vom beobachteten Ort abhängen. Diese sind an allen Orten im Kosmos gleich, wenn sie vom selben Ort aus beobachtet werden. Dazu gehört beispielsweise die Geschwindigkeit der :
In diesem Fall kann in Formeln der beobachtete Ort weggelassen werden, denn er spielt keine Rolle.
Wirkungsquanten-Bewegungsraum
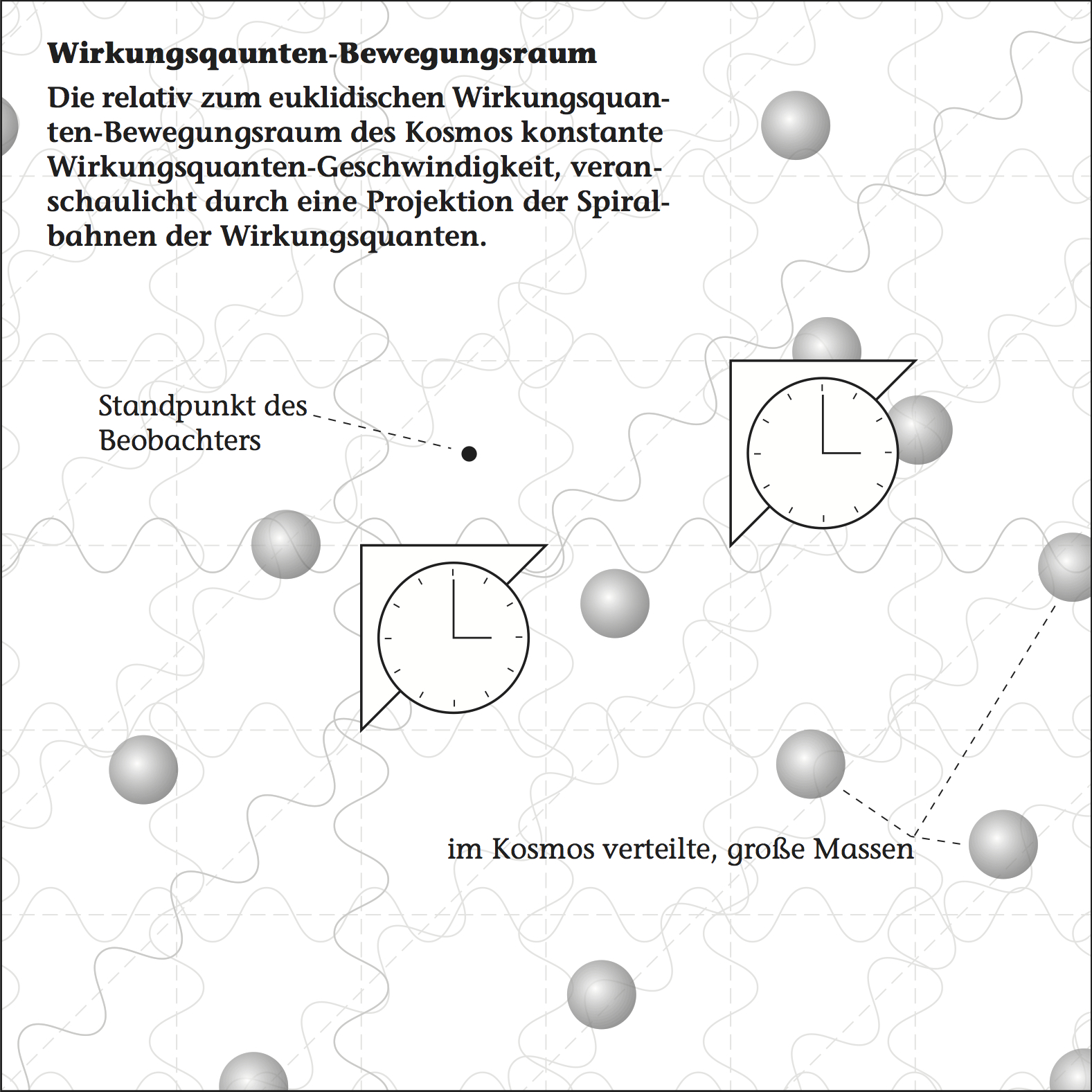
Die Perspektive, aus der heraus die Geschwindigkeit der als konstant erscheint ist der Wirkungsquanten-Bewegungsraum. Der Raum ist aus dieser Perspektive immer euklidisch flach.
Der Eindruck der Raumzeitkrümmung ergibt sich hier aus strukturellen und dynamischen Gründen: Die Dichte der Wirkungsquanten in Relation zu ihrer konstanten Bewegung variiert aus dieser Sicht genauso wie die Geschwindigkeit des Lichts oder der lichtähnlichen Strukturen in Relation zur konstanten Bewegung der Wirkungsquanten.
Auch die relative Dichteveränderung von hintereinander herlaufenden lichtähnlichen Teilchen, wie polarisierte Photonen, unpolarisierte Photonen des Vakuums – die Vakuum-Elapsonen –, oder ähnliche Strukturen in Materie-Elementarteilchen, verhält sich wie die relative Veränderung der Lichtgeschwindigkeit.
Die Raumzeitkrümmung der Allgemeinen Relativitätstheorie ebenso wie ihre gravitative Zeitdilatation erscheinen im Wirkungsquanten-Bewegungsraum also als Veränderung der dynamischen Strukturen des Vakuums und der Elementarteilchen in Relation zu den Verhältnissen beim Beobachter. Eine aus Sicht eines Beobachters verändert erscheinende Lichtgeschwindigkeit ist auch im Rahmen der Allgemeinen Relativitätstheorie als Shapiro-Verzögerung bekannt. Im Wirkungsquanten-Bewegungsraum gibt es diesbezüglich Besonderheiten, auf die wir gleich noch zu sprechen kommen.
Aus Sicht des nimmt die konstante einen Wert an, der in einem besonderen Verhältnis zur Lichtgeschwindigkeitskonstanten steht, wie wir noch sehen werden:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {^{0}v_{wq}}\;\;\;=\;\;\;\sqrt{ 2 } \cdot {_{\raise -.3ex 0}c} } \] | () |
Eine Besonderheit des Wirkungsquanten-Bewegungsraums ist, dass die Dichte der Wirkungsquanten an einem beobachteten Ort nicht in allen Richtungen gleich ist. Sie kann sich am selben Ort je nach Richtung unterscheiden. Daraus folgt auch, dass die effektive Geschwindigkeit des Lichts nicht am selben Ort in allen Richtungen gleich groß ist, sie ist anisotrop.
In der späteren Herleitung der Quantengravitation in der Quanten-Fluss-Theorie und ihrer Variabilität der Lichtgeschwindigkeit in der Schwarzschild-Metrik ergibt sich die Richtungsabhängige Veränderung der Lichtgeschwindigkeit zu:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {_{r,p}c_{mas}}\;\;\;=\;\;\;{_{\raise -.3ex 0}c} \cdot \left( 1 - 2 \cdot \frac{G \cdot M}{{_{\raise -.3ex 0}c}^{2} \cdot r} \right)^{p} } \] | (QGra.LV.106) |
Die Variable p in der Potenz besitzt dabei im Fall tangentialer Richtung der Lichtausbreitung zur zentralen Masse den Wert p = 1/2 und im Fall radialer Richtung den Wert p = 1. Hier steht r für den Abstand zum Zentrum der Masse. Das vorangestellte r,p vor der variablen Lichtgeschwindigkeit r,pcmas drückt also ihren Orts- und Richtungsbezug aus.
An Orten des kosmischen Beobachters selber stellt sich die variable Lichtgeschwindigkeit übrigens als isotrop dar.
Beim Wirkungsquanten-Bewegungsraum haben wir es mit einer Perspektive zu tun, die davon ausgeht, dass aus Sicht des kosmischen Beobachters, am Standpunkt durchschnittlicher Energiedichte des Vakuums, der effektive Wert der Lichtgeschwindigkeit dem Wert der Lichtgeschwindigkeitskonstanten 0c gleich ist:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {_{\raise -.3ex 0}c}\;\;\;=\;\;\;{c_{\raise -.3ex 0}} } \] | () |
Im Folgenden gehen wir zu Perspektiven über, die den Richtungsbezug der Lichtausbreitung nicht mehr besitzen.
Licht-Bewegungsraum
Beim Licht-Bewegungsraum haben wir es mit einer Perspektive zu tun, die den Wirkungsquanten-Bewegungsraum so verändert, dass die variable Lichtgeschwindigkeit an einem Ort immer in allen Richtungen isotrop ist. Dies wird dadurch erreicht, dass der Raum so gekrümmt wird, dass dies gewährleistet ist.
Da die Korrektur der Raumdehnung in Richtung einer isotropen, variablen Lichtgeschwindigkeit auf verschiedene Arten möglich ist, definiere ich hier, dass die Dehnung oder Stauchung des Raums in radialer Richtung zu einer Zentralmasse geschieht. Die Raumdehnung und die variable Lichtgeschwindigkeit in tangentialer Richtung bleibt davon unberührt.
Im nächsten Schritt soll nun beschrieben werden, wie der Übergang der Perspektiven zur Raumzeitkrümmung der Allgemeinen Relativitätstheorie vollzogen wird.
Raumzeitkrümmung der Allgemeinen Relativitätstheorie
In der bekannten Perspektive der Allgemeinen Relativitätstheorie wird nun noch eine vierte, imaginäre Raumdimension hinzugefügt in der eine Bewegung möglich ist, sodass die Lichtgeschwindigkeit auch effektiv immer als Konstante erscheint:
Bewegt sich Licht effektiv langsamer oder schneller als die Lichtgeschwindigkeitskonstante, dann dehnt sich der dreidimensionale Raum so, dass seine Geschwindigkeit den Wert der Lichtgeschwindigkeitskonstanten annimmt. Bewegen sich materielle Punkte durch den Raum, dann wird deren fehlender oder überschüssiger Anteil an der Lichtgeschwindigkeitskonstanten in der imaginären Zeitdimension so ergänzt, dass sich seine komplette Bewegungsgeschwindigkeit zur Lichtgeschwindigkeitskonstanten ergibt.
Im Licht-Bewegungsraum, der aus dem Wirkungsquanten-Bewegungsraum entwickelt wird, sind zwischen sehr großen Massen auch variable Lichtgeschwindigkeiten möglich, die bis nah heran an das √2-fache der Lichtgeschwindigkeitskonstanten reichen können. Diese Eigenschaft der Quanten-Fluss-Theorie und ihrer Quantengravitation, die mit ihrer variablen Vakuum-Energie um sehr große Massen herum zu tun hat, eröffnet eine wichtige Perspektive zur Lösung des Phänomens der Dunklen Materie.
Eine Lösung der Darstellung des Licht-Bewegungsraums in der Raumzeitkrümmung der Allgemeinen Relativitätstheorie sollte demnach die Wirkung des Phänomens der Dunklen Materie so sinnvoll abbilden und die Allgemeine Relativitätstheorie auf diese Weise modifizieren.
Weitere Vorgehensweise
Um die Formeln der folgenden Kapitel zu vereinfachen und dadurch leserlicher und verständlicher zu machen wird, wo sinnvoll, versucht, die Beobachtungen aus Sicht des kosmischen Beobachters zu beschreiben. Um den Beobachtungsstandpunkt auf beliebige Beobachter zu erweitern, siehe Kapitel .
| → |
|
| |
Zeit |
|
Die Bewegung der Wirkungsquanten entspricht dem Lauf der grundlegenden Zeit, dem einer Normaluhr
| ← |
|
(• Die Konstanz der Wirkungsquanten-Geschwindigkeit ergibt sich nur im euklidischen Wirkungsquanten-Bewegungsraum! Die Konstanz der LG gilt nur im gekrümmten Licht-Bewegungsraum.)
(Einpflegen: Titel in kosmische Zeit ändern? Der Begriff kosmische Zeit wird speziell verwendet, siehe hier. Kosmische Uhr und kosmische Zeit sollten an diese Stelle erwähnung finden. Die Auflösung des ›Problems der Gleichzeitigkeit‹ erwähnen!)
Die nachfolgenden Erklärungen werden aus Sicht eines beschrieben.
|
Die räumlich absolute und jeder Veränderung entsprechende Zeit der relativistischen Quantenfeldtheorie entsteht aus der Bewegung der Wirkungsquanten (wq), die das Vakuum und alle Elementarteilchen bilden. Der Weg wwq, den ein Wirkungsquant zurück legt, ist proportional zur seit Beginn des Wegs verstrichenen Zeit t:
Die eingeführte Proportionalitätskonstante ist die in der Hypothese zunächst als konstant angenommene Wirkungsquanten-Geschwindigkeit vwq. Die grundlegende Zeit, nachfolgend nur noch t genannt, entspringt folglich der Positionsveränderung der Wirkungsquanten des Bewegungsraums (siehe ).
Diese Bewegung nimmt der kosmische Beobachter aus diesem Grund logischer Weise an jedem Ort im Kosmos gleich wahr:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {_{y}v_{wq}}\;\;\;=\;\;\;{_{x}v_{wq}}\;\;\;=\;\;\;{v_{wq}} } \] | (ZAF.Zt.4) |
Paradigmenwechsel: Die Quanten-Fluss-Theorie vollzieht an dieser Stelle einen beinahe unmerklichen Paradigmenwechsel. Struktur und Bewegung werden zur Grundlage von Raum und Zeit. Den der Weg der Wirkungsquanten entspricht der Veränderung ihrer Position im Verhältnis zur aktuellen strukturellen Verteilung der Wirkungsquanten im Raum. Und diese Veränderung meint Bewegung. Das Maß für Raum und Zeit entspringt also der Bewegung in einer Struktur. Nur auf diese Weise ist es möglich, dass nachfolgend aus unterschiedlichen Bewegungskomponenten verschiedene Aspekte von Zeit entstehen, die zur Lösung des ›Problems der Zeit‹ führen.
In der bisherigen Physik versteht man, im Gegensatz dazu, Raum und Zeit als gegebene Größen aus denen die Bewegung entsteht.
Die Wirkungsquanten-Bewegung findet man als Äquivalent der Zeit im Wirkungsquanten-String jedes Elementarteilchens und so auch in den Wirkungsquanten-Strings des Vakuums – den Vakuum-Elapsonen – wieder. Daher sind alle Elementarteilchen und das Vakuum mit Zeit verknüpft.
Ein anderer Aspekt der Zeit, der im nächten Kapitel beschrieben wird, ist die je nach wirkender Gravitation variable .
| → |
|
| |
Alterung und strukturierter Raum |
|
Die Bewegung des Lichts entspricht dem Lauf der Alterung, einer variablen Gravitationsuhr
| ← |
|
Die nachfolgenden Erklärungen werden aus Sicht eines beschrieben.
|
|
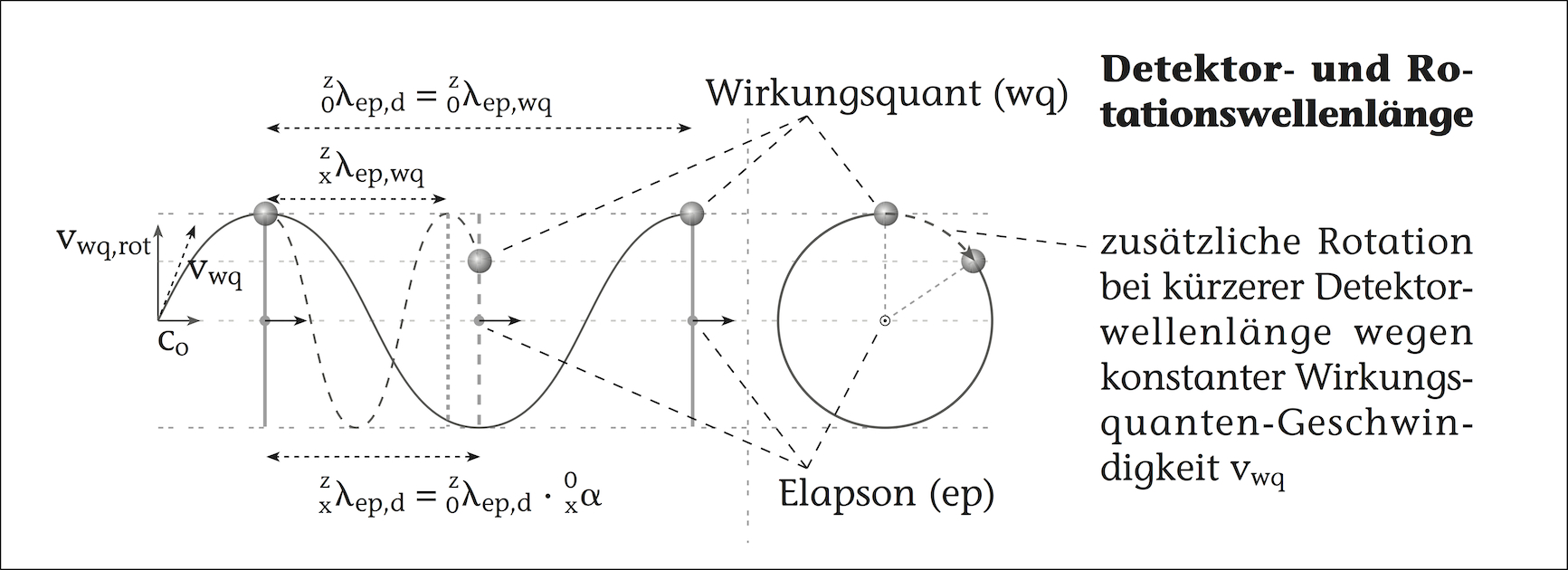
Anders als die räumlich absolute der relativistischen Quantenfeldtheorie entsteht die Alterung – die Zeit der Allgemeinen Relativitätstheorie – aus der Bewegung des Lichts; der Photonen (ph), der Vakuum-Elapsonen (ep) und vergleichbarer Wirkungsquanten-String-Strukturen der Elementarteilchen der Materie. Allgemeiner ist zu sagen, der Weg wph, den das Licht im Verhältnis zur Lichtstruktur des strukturierten Raums zurück legt, ist proportional zur seit Beginn dieses Wegs fortgeschrittenen Alterung a. In und entspricht dieser Weg dem Vorwärtsschrauben der Helixspiralbahn – ihrer Translation:
Der Strukturfaktor k des strukturellen Kontexts am Ort x trägt zusätzlich noch ein p für seine Richtungsabhängigkeit. k verkörpert in der Quanten-Fluss-Theorie so gemeinsam mit der variablen Lichtgeschwindigkeit die Raumzeitkrümmung der Allgemeinen Relativitätstheorie. Die Raumzeitkrümmung wird in der neuen Theorie so durch eine reale Verzerrung der Feinstruktur des Vakuums und der Elementarteilchen in Bezug auf die Wirkungsquanten-Struktur des an sich dargestellt.
Da die Zeit t im Kosmos an allen Orten konstant läuft, die Alterung hingegen nicht, entspricht der linke Term der Formel – die Alterung pro Zeit – einem ortsabhängigen Alterungsfaktor ⍺ (Alpha), während der rechte Term – der Weg des Lichts pro Zeit im strukturellen Kontext k – der ortsüblichen Lichtgeschwindigkeit c im strukturierten Raum aus Sicht des entspricht. Die Lichtgeschwindigkeit in der Wirkungsquanten-Struktur des Kosmos, ohne die Berücksichtigung des strukturellen Kontexts seiner Lichtstruktur, ist dann schlicht der Weg des Lichts pro Zeit t des Kosmos:
Die hier berechnete Lichtgeschwindigkeit xc ist dabei um ihre Richtungsabhängigkeit vom strukturellen Kontext bereinigt. Sie ist proportional zur Alterung der Elementarteilchen am Ort x. Wohingegen x,pc die richtungsabhängige Lichtgeschwindigkeit in Bezug auf die Wirkungsquanten-Struktur des Kosmos ist.
Aus der Sicht des kosmischen Beobachters B0 gleicht seine eigene Alterung seiner Zeit. Dabei läuft die Zeit t an jedem Ort gleich:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {_{\raise -.3ex 0}a}\;\;\;=\;\;\;t } \] | (ZAF.Alt.8) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\frac{ {_{\raise -.3ex 0}a} }{ t }\;\;\;=\;\;\;1 } \] | (ZAF.Alt.9) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow {_{\raise -.3ex 0}\alpha}\;\;\;=\;\;\;1 } \] | (ZAF.Alt.10) | ||
Diese Orte des kosmischen Beobachters sind Orte . Aus diesem Grund bewegt sich das Licht an diesen Orten in Größe der Lichtgeschwindigkeitskonstanten c0 in der Lichtstruktur des Raums:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {_{\raise -.3ex 0}c}\;\;\;=\;\;\;{c_{\raise -.3ex 0}} } \] | (ZAF.Alt.11) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}\frac{ {_{\raise -.3ex 0}c} }{ {_{\raise -.3ex 0}\alpha} }\;\;\;=\;\;\;\frac{ {_{x}c} }{ {_{x}\alpha} } } \] | (ZAF.Alt.12) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{\raise -.3ex 0}c}\;\;\;=\;\;\;\frac{ {_{x}c} }{ {_{x}\alpha} } } \] | (ZAF.Alt.13) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{x}c}\;\;\;=\;\;\;{_{\raise -.3ex 0}c} \cdot {_{x}\alpha} } \] | (ZAF.Alt.14) | ||
Über den Alterungsfaktor ⍺ kommt man so auf die variable Lichtgeschwindigkeit im Gravitationsfeld am Ort x.
Wegen der Formeln und ergibt sich Äquivalentes für die Alterung:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow {_{x}a}\;\;\;=\;\;\;{_{\raise -.3ex 0}a} \cdot {_{x}\alpha} } \] | (ZAF.Alt.15) |
Die Lichtbewegung findet man als Äquivalent der Alterung im Wirkungsquanten-String jedes Elementarteilchens und in den Wirkungsquanten-Strings des Vakuums wieder. Daher sind alle Elementarteilchen und das Vakuum mit Zeit und Alterung verknüpft. Konkret ergibt sich der Alterungsfaktor aus der Quantengravitation der Elementarteilchen und allgemeiner aus der kosmischen Quantengravitation, welche das Phänomen der Dunklen Materie einschließt. Die erster Näherung der später entwickelten, neuen Quantengravitation der Elementarteilchen ergibt genau die Gravitation der Allgemeinen Relativitätstheorie.
Im folgenden Kapitel wird gezeigt, wie aus der Zeit und der Alterung die eines Elementarteilchens hervorgeht.
| → |
|
| |
Frequenz und Energie |
|
Der Zusammenhang zwischen Alterungszeit und Frequenz im Gravitationsfeld
| ← |
|
| ▾ | Notizen |
• Kapitel überarbeiten!
• Wie ist es mit der Frequenz und Energie bei bewegten Materie-Elementarteilchen? Dort gibt es auch einen scheinbaren Widerspruch, denn schneller bewegen heißt verlangsamte Zeit also geringere Frequenz, aber auch mehr Energie höhere Frequenz? Er löst diesen Widerspruch durch zwei Frequenzen, steht dort. Die innere Frequenz ist die Compton-Frequenz, wenn ich richtig verstehe, und die äußere ist die Materiewelle. »Nur letztere [die Materiewelle] erfüllt die Bedingung, dass ihre Frequenz der Gesamtenergie (mit Einschluss der kinetischen und potentiellen) direkt proportional ist.«
• Umfang einer Ellipse (Bogenlänge): Wikipedia. Ellipse. Formelsammlung (Flächeninhalt und Umfang). Umfang.
Die nachfolgenden Erklärungen werden aus Sicht eines beschrieben.
Als weitere Bewegungskomponente der helixförmigen Spiralbewegung der Wirkungsquanten findet man ihre Rotationsgeschwindigkeit, die über den mittleren Umfang des Photons uph zur inneren Frequenz fph führt (siehe ).
Dabei gehe ich von einer Frequenz aus, die von der Bewegungsrichtung des Lichts unabhängig ist. Diese Annahme lässt sich zum einen damit begründen, dass die reine Richtungsänderung eines Photons, beispielsweise durch die Reflexion an einem Spiegel oder durch gravitative Lichtbeugung, keinen Einfluss auf seine Energie und damit auf seine Frequenz hat. Zum anderen würde sich ein logischer Bruch innerhalb der Quanten-Fluss-Theorie ergeben, wenn dies nicht so wäre. Denn der String eines Materie-Elementarteilchens, dessen Lichtbahn in ganz unterschiedlichen Raumrichtungen verläuft, muss an allen Stellen gleich schnell schwingen, sonst würde er zerreißen.
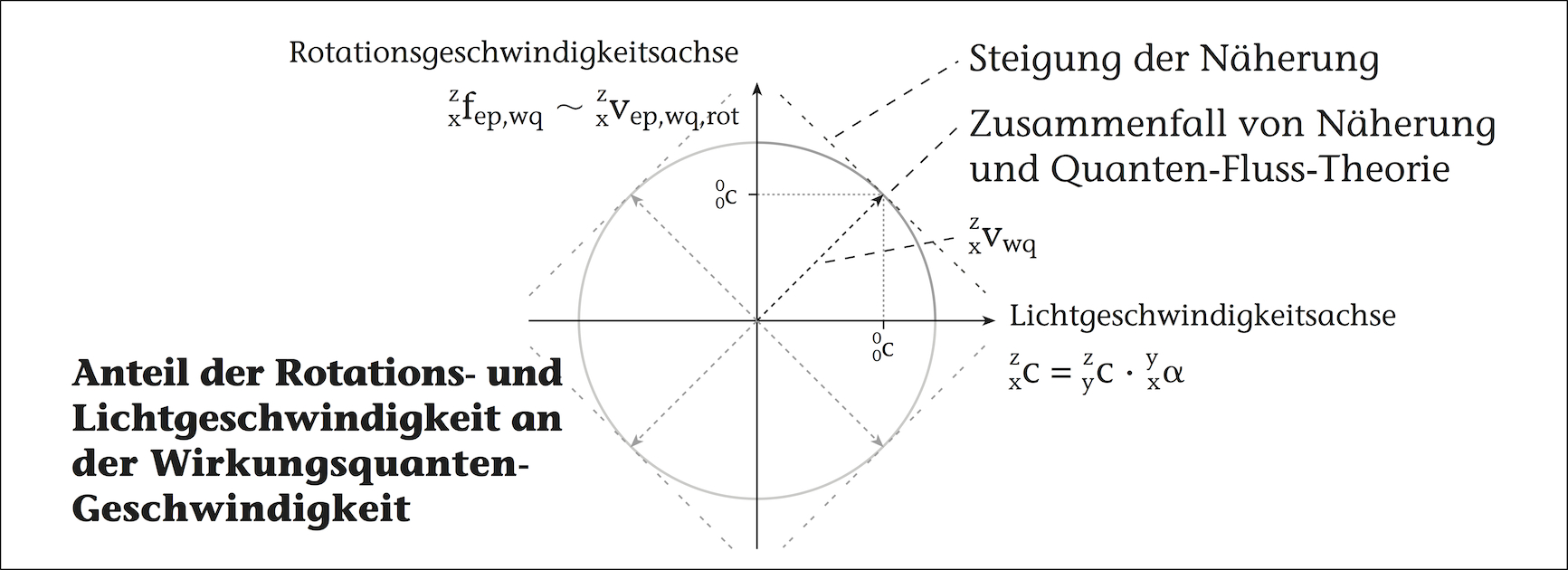
Über den Phytagoras stehen die örtliche, richtungsabhängige Rotations- und , vwq,rot und c, mit der vwq im Zusammenhang:
(Darauf eingehen – ggf. im extra Kapitel –, dass die Geometrie des Umfangs in bestimmten Situationen – an den Orten der kosmischen Beobachter und generell bei radialer Bewegungsrichtung in Bezug auf eine Zentralmasse – ein Kreis ist. Die begonnene Analyse zum Umfang dort einpflegen.)
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {v_{wq}}\;\;\;=\;\;\;\sqrt{ {_{x,p}v_{wq,rot}^{2}} + {_{x,p}c^{2}} } } \] | (ZAF.FE.1) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {_{x,p}v_{wq,rot}}\;\;\;=\;\;\;{_{x}f_{ph}} \cdot {_{x,p}u_{ph}} } \] | (ZAF.FE.2) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}{v_{wq}}\;\;\;=\;\;\;\sqrt{ ({_{x}f_{ph}} \cdot {_{x,p}u_{ph}})^{2} + {_{x,p}c^{2}} } } \] | (ZAF.FE.3) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{v_{wq}^{2}}\;\;\;=\;\;\;({_{x}f_{ph}} \cdot {_{x,p}u_{ph}})^{2} + {_{x,p}c^{2}} } \] | (ZAF.FE.4) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{v_{wq}^{2}} - {_{x,p}c^{2}}\;\;\;=\;\;\;({_{x}f_{ph}} \cdot {_{x,p}u_{ph}})^{2} } \] | (ZAF.FE.5) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\sqrt{ {v_{wq}^{2}} - {_{x,p}c^{2}} }\;\;\;=\;\;\;{_{x}f_{ph}} \cdot {_{x,p}u_{ph}} } \] | (ZAF.FE.6) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{x}f_{ph}}\;\;\;=\;\;\; \frac{ \sqrt{ {v_{wq}^{2}} - {_{x,p}c^{2}} } }{ {_{x,p}u_{ph}} } } \] | (ZAF.FE.7) | ||
Die innere Frequenz findet sich sowohl im Wirkungsquanten-String jedes Elementarteilchens als auch in den Wirkungsquanten-Strings des Vakuums wieder. Daher sind alle Elementarteilchen und das Vakuum mit Zeit, Alterung, Frequenz und Energie verknüpft.
Die Helixbahnhypothese führt so zu einer nach meinem Wissen bisher unbekannten Abhängigkeit zwischen der inneren Frequenz und der Alterungszeit.
Auf diese Weise löst sich sowohl der scheinbare Widerspruch zwischen innerer Frequenz und Zeit als auch das ›Problem der Zeit‹ auf.
Im nachfolgenden Kapitel wird die vwq aus dem Pound-Rebka-Snider-Experiment berechnet. Setzt man diese hier ein, so ergibt sich, mit Hilfe der Formeln und , folgende Vereinfachung. Um dabei die Formeln nicht zu kompliziert zu gestallten, wird mit um den bereinigten Größen gearbeitet:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {v_{wq}}\;\;\;=\;\;\;\sqrt{ 2 } \cdot {c_{0}}\;\;\;=\;\;\;\sqrt{ 2 } \cdot {_{\raise -.3ex 0}c} } \] | () | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {_{x}f_{ph}}\;\;\;=\;\;\; \frac{ \sqrt{ {v_{wq}^{2}} - {_{x}c^{2}} } }{ {_{x}u_{ph}} } } \] | (ZAF.FE.8) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}{_{x}f_{ph}}\;\;\;=\;\;\;\frac{ \sqrt{ \Bigl( \sqrt{ 2 } \cdot {_{\raise -.3ex 0}c} \Bigr)^2 - {_{x}c}^{2} } }{ {_{x}u_{ph}} } } \] | (ZAF.FE.9) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{x}f_{ph}}\;\;\;=\;\;\;\frac{ \sqrt{ 2 \cdot {_{\raise -.3ex 0}c}^2 - \Bigl( {_{\raise -.3ex 0}c} \cdot {_{x}\alpha} \Bigr)^{2} } }{ {_{x}u_{ph}} } } \] | (ZAF.FE.10) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{x}f_{ph}}\;\;\;=\;\;\;\sqrt{ 2 - {_{x}\alpha}^{2} } \cdot \frac{ {_{\raise -.3ex 0}c} }{ {_{x}u_{ph}} } } \] | (ZAF.FE.11) | ||
So ergibt sich die Frequenz in Abhängigkeit vom Alterungsfaktor.
Die innere Frequenz ist über Plancks Proportionalität von Energie und Frequenz proportional zur Energie eines Elementarteilchens(Link genauer). Dies ergibt sich in der Quanten-Fluss-Theorie auf natürliche Weise aus einem prinzipiellen Abzählproblem der Wirkungsquanten beim Messen der Energie des Elementarteilchens:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {_{x}E}\;\;\;=\;\;\;{_{x}f} \cdot h } \] | (Un.10) |
Die Energie eines Elementarteilchens steht mit der Vakuumenergiedichte am Ort seines Aufenthalts im Zusammenhang, wie sich zeigen wird. Da die Vakuumenergiedichte der im Raum entspricht, stößt man dadurch letztendlich auf die Struktur Schwarzer Löcher.
Welch starken Realitätsbezug die helixförmige Spiralbahn der Wirkungsquanten hat, wird sich im Verlauf der Entwicklung der Quanten-Fluss-Theorie klar verdeutlichen. Ein wichtiger Schritt wird im folgenden Kapitel mit der Herleitung der aus dem Pound-Rebka-Snider-Experiment getan.
| → |
|
| |
Wirkungsquanten-Geschwindigkeit |
|
Die erhöhte Lichtgeschwindigkeit, eine neue fundamentale Konstante – die Lichtgeschwindigkeit in neuem Gewand, ein Drilling wird geboren
| ← |
|
| ▾ | Notizen |
• Eine Berechnung der gravitativen Rotverschiebung findet sich auch in Variable Lichtgeschwindigkeit in der Allgemeinen Relativitätstheorie, siehe auch Datei "Variable Lichtgeschwindigkeit in der Allgemeinen Relativitätstheorie.pdf".
Die nachfolgenden Erklärungen werden aus Sicht eines beschrieben.
|
|
Um die Größe der Wirkungsquanten-Geschwindigkeit vwq zu erhalten, ist es möglich die Rotationsgeschwindigkeit der Wirkungsquanten vwq,rot zu bestimmen und erstere daraus zu berechnen, wie die und die Formel verdeutlichen. Denn die örtliche Lichtgeschwindikeit c wird als gegeben angesehen, weil sie sich aus der Quantengravitation der Elementarteilchen ergibt:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {v_{wq}}\;\;\;=\;\;\;\sqrt{ {_{x,p}v_{wq,rot}^{2}} + {_{x,p}c^{2}} } } \] | () |
Es würde also sehr weiter helfen, wenn man etwas über das Verhältnis der Rotationsgeschwindigkeit zur örtlichen Lichtgeschwindigkeit herausfindet.
Das Pound-Rebka-Snider-Experiment
Das Pound-Rebka-Snider-Experiment (Erwähnen! Das Pound-Rebka-Snider-Experiment und Maser-Experimente messen die gravitative Rot- und Blauverschiebung einer Lichtwelle, also die Detektorfrequenz einer Lichtwelle und nicht die innere Frequenz eines Photons. Messen Atomuhren die innere Frequenz von Materie-Elementarteilchen? Bei geringer Gravitation fallen beide Messergebnisse zusammen, aber bei hoher Gravitation nicht! (Graph erstellen?) Zur Verifikation wird der Zusammenfall bei geringer Gravitation an der Erdoberfläche oder im Weltraum nahe der Erde benutzt.) – und verwandte Experimente, zusammenfassend einfach Pound-Rebka-Snider-Experiment genannt – bringt die örtliche Lichtgeschwindigkeit mit der inneren Frequenz in Verbindung. Das Experiment untersucht diesbezüglich, wie sich die relative Frequenzänderung yx𝝂ph bei der Bewegung im Gravitationsfeld vom Ort y zum Ort x verhält:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {_{\overline{yx}}\nu_{ph}}\;\;\;=\;\;\;\frac{ {_{x}f_{ph}} - {_{y}f_{ph}} }{ {_{y}f_{ph}} } } \] | (ZAF.Wq.1) |
Die Formel macht deutlich, dass diese relative Frequenzänderung unabhängig vom Beobachterstandort ist, weil ein Wechsel des Beobachterstandorts als Faktor in alle drei Frequenzen eingeht und sich so wegkürzt.
Wie durch das Pound-Rebka-Snider-Experiment bestätigt wurde, fällt die relative Frequenzänderung eines Elementarteilchens bei Annäherung an eine große Masse äußerst klein und positiv aus:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { 0\;\;\;<\;\;\;{_{\overline{yx}}\nu_{ph}}\;\;\;\ll\;\;\;1 } \] | (ZAF.Wq.2) |
Aus Sicht der Allgemeinen Relativitätstheorie bestätigt das Pound-Rebka-Snider-Experiment, dass der relative Alterungsfaktor ⍺ auf der Erdoberfläche hinreichend genau in der gleichen Größenordnung von Eins ausgehend kleiner wird, wie die relative Frequenzdifferenz yx𝝂ph größer wird. Deshalb kann folgende Näherung angenommen werden. (Besser herleiten! Diese Näherung ergibt sich daraus, dass die Detektorfrequenz einer Lichtwelle und die innere Frequenz eines Photons bei sehr geringer Gravitation, z. B. an der Erdoberfläche, zusammenfallen.) Die Bedeutung hochgestellter Orte wird in den Abschnitten und beschreiben:
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {^{y}_{y}\alpha}\;\;\;=\;\;\;1 } \] | (ZAF.Wq.3) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}\frac{ {_{x}c} }{ {_{y}c} }\;\;\;=\;\;\;{^{y}_{x}\alpha}\;\;\;\approx\;\;\;{^{y}_{y}\alpha} - {_{\overline{yx}}\nu_{ph}} } \] | (ZAF.Wq.4) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{^{y}_{x}\alpha}\;\;\;\approx\;\;\;1 - {_{\overline{yx}}\nu_{ph}} } \] | (ZAF.Wq.5) | ||
Die relative Frequenzänderung aus Formel kann zur weiteren Entwicklung mit Hilfe der Formeln und umgeschrieben werden, wobei sich der Nenner aller eingesetzten Frequenzen wegkürzt. Durch Einsetzen der Näherung ergibt sich dann:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {_{x}f_{ph}}\;\;\;=\;\;\; \frac{ \sqrt{ {v_{wq}^{2}} - {_{x,p}c^{2}} } }{ {_{x,p}u_{ph}} } } \] | () | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}{_{\overline{yx}}\nu_{ph}}\;\;\;=\;\;\;}{ \frac{ \sqrt{ {v_{wq}^{2}} - {_{x,p}c^{2}} } - \sqrt{ {v_{wq}^{2}} - {_{y,p}c^{2}} } }{ \sqrt{ {v_{wq}^{2}} - {_{y,p}c^{2}} } } } \] | (ZAF.Wq.6) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{\overline{yx}}\nu_{ph}} \cdot \sqrt{ {v_{wq}^{2}} - {_{y,p}c^{2}} }\;\;\;=\;\;\;}{ \sqrt{ {v_{wq}^{2}} - {_{x,p}c^{2}} } - \sqrt{ {v_{wq}^{2}} - {_{y,p}c^{2}} } } \] | (ZAF.Wq.7) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{\overline{yx}}\nu_{ph}} \cdot \sqrt{ {v_{wq}^{2}} - {_{y,p}c^{2}} } + \sqrt{ {v_{wq}^{2}} - {_{y,p}c^{2}} }\;\;\;=\;\;\;}{ \sqrt{ {v_{wq}^{2}} - {_{x,p}c^{2}} } } \] | (ZAF.Wq.8) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}({_{\overline{yx}}\nu_{ph}} + 1) \cdot \sqrt{ {v_{wq}^{2}} - {_{y,p}c^{2}} }\;\;\;=\;\;\;\sqrt{ {v_{wq}^{2}} - {_{x,p}c^{2}} } } \] | (ZAF.Wq.9) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}({_{\overline{yx}}\nu_{ph}} + 1)^2 \cdot ({v_{wq}^{2}} - {_{y,p}c^{2}})\;\;\;=\;\;\;{v_{wq}^{2}} - {_{x,p}c^{2}} } \] | (ZAF.Wq.10) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}({_{\overline{yx}}\nu_{ph}} + 1)^2 \cdot {v_{wq}^{2}} - ({_{\overline{yx}}\nu_{ph}} + 1)^2 \cdot {_{y,p}c^2}\;\;\;=\;\;\;}{ {v_{wq}^{2}} - {_{x,p}c^2} } \] | (ZAF.Wq.11) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{x,p}c^2} - ({_{\overline{yx}}\nu_{ph}} + 1)^2 \cdot {_{y,p}c^2}\;\;\;=\;\;\;}{ {v_{wq}^{2}} - ({_{\overline{yx}}\nu_{ph}} + 1)^2 \cdot {v_{wq}^{2}} } \] | (ZAF.Wq.12) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{y,p}c^2} \cdot {^{y}_{x}\alpha^2} - ({_{\overline{yx}}\nu_{ph}} + 1)^2 \cdot {_{y,p}c^2}\;\;\;=\;\;\;}{ {v_{wq}^{2}} - ({_{\overline{yx}}\nu_{ph}} + 1)^2 \cdot {v_{wq}^{2}} } \] | (ZAF.Wq.13) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{y,p}c^2} \cdot \left({^{y}_{x}\alpha^2} - ({_{\overline{yx}}\nu_{ph}} + 1)^2\right)\;\;\;=\;\;\;}{ {v_{wq}^{2}} \cdot \left(1 - ({_{\overline{yx}}\nu_{ph}} + 1)^2\right) } \] | (ZAF.Wq.14) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\frac{ {v_{wq}^{2}} }{ {_{y,p}c^2} }\;\;\;=\;\;\;}{ \frac{ {^{y}_{x}\alpha^2} - ({_{\overline{yx}}\nu_{ph}} + 1)^2 }{ 1 - ({_{\overline{yx}}\nu_{ph}} + 1)^2 } } \] | (ZAF.Wq.15) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}\frac{ {v_{wq}^{2}} }{ {_{y,p}c^2} }\;\;\;\approx\;\;\;}{ \frac{ (1 - {_{\overline{yx}}\nu_{ph}})^2 - ({_{\overline{yx}}\nu_{ph}} + 1)^2 }{ 1 - ({_{\overline{yx}}\nu_{ph}} + 1)^2 } } \] | (ZAF.Wq.16) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\frac{ {v_{wq}^{2}} }{ {_{y,p}c^2} }\;\;\;\approx\;\;\;}{ \frac{ 1 - 2 \cdot {_{\overline{yx}}\nu_{ph}} + {_{\overline{yx}}\nu_{ph}^2} }{ 1 - ({_{\overline{yx}}\nu_{ph}} + 1) } }{ - \frac{ {_{\overline{yx}}\nu_{ph}^2} + 2 \cdot {_{\overline{yx}}\nu_{ph}} + 1 }{ 1 - ({_{\overline{yx}}\nu_{ph}} + 1)^2 } } \] | (ZAF.Wq.17) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\frac{ {v_{wq}^{2}} }{ {_{y,p}c^2} }\;\;\;\approx\;\;\;}{ \frac{ - 4 \cdot {_{\overline{yx}}\nu_{ph}} }{ 1 - ({_{\overline{yx}}\nu_{ph}^2} + 2 \cdot {_{\overline{yx}}\nu_{ph}} + 1) } } \] | (ZAF.Wq.18) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\frac{ {v_{wq}^{2}} }{ {_{y,p}c^2} }\;\;\;\approx\;\;\;}{ \frac{ 4 \cdot {_{\overline{yx}}\nu_{ph}} }{ {_{\overline{yx}}\nu_{ph}^2} + 2 \cdot {_{\overline{yx}}\nu_{ph}} } } \] | (ZAF.Wq.19) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\frac{ {v_{wq}^{2}} }{ {_{y,p}c^2} }\;\;\;\approx\;\;\;}{ \frac{ 2 }{ \frac{1}{2} \cdot {_{\overline{yx}}\nu_{ph}} + 1 } } \] | (ZAF.Wq.20) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{v_{wq}}\;\;\;\approx\;\;\;\sqrt{ \frac{ 2 }{ \frac{1}{2} \cdot {_{\overline{yx}}\nu_{ph}} + 1 } } \cdot {_{y,p}c} } \] | (ZAF.Wq.21) | ||
Die Verhältnisse auf der Erdoberfläche
Weil die relative Frequenzänderung, wie in Formel dargestellt, sehr klein ausfällt, kann sie nun als Null angenommen werden. Weiter ist davon auszugehen, dass der im Kosmos absolute Alterungsfaktor ⍺ der Erdoberfläche sehr nahe bei Eins liegt. Denn die Gravitation an der Erdöberfläche ist extrem gering für kosmische Verhältnisse, sodass wir uns nahezu als sehen dürfen. Die Verzerrung des verschwindet aus diesem Grund nahezu, so dass der Richtungsparameter p vernachlässigbar wird. Und es gilt dann Formel :
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}{_{\overline{yx}}\nu_{ph}}\;\;\;\approx\;\;\;0 } \] | (ZAF.Wq.22) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}{_{y}\alpha}\;\;\;\approx\;\;\;1 } \] | (ZAF.Wq.23) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}{_{y,p}c}\;\;\;\approx\;\;\;{_{y}c} } \] | (ZAF.Wq.24) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}{v_{wq}}\;\;\;\approx\;\;\;\sqrt{ \frac{ 2 }{ \frac{1}{2} \cdot 0 + 1 } } \cdot {_{y}c} } \] | (ZAF.Wq.25) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{v_{wq}}\;\;\;\approx\;\;\;\sqrt{ 2 } \cdot {_{\raise -.3ex 0}c} \cdot {_{y}\alpha} } \] | (ZAF.Wq.26) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{v_{wq}}\;\;\;\approx\;\;\;\sqrt{ 2 } \cdot {_{\raise -.3ex 0}c} \cdot 1 } \] | (ZAF.Wq.27) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{v_{wq}}\;\;\;\approx\;\;\;\sqrt{ 2 } \cdot {_{\raise -.3ex 0}c} } \] | (ZAF.Wq.28) | ||
Für Orte eines kosmischen Beobachters wird letztendlich die Gleichheit angenommen:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}{v_{wq}}\;\;\;=\;\;\;\sqrt{ 2 } \cdot {_{\raise -.3ex 0}c} } \] | (ZAF.Wq.29) |
Wegen des Postulats der konstanten Wirkungsquanten-Geschwindigkeit gilt diese Formel im gesamten Kosmos. Dabei steht die Wirkungsquanten-Geschwindigkeit für die neue, erhöhte Lichtgeschwindigkeit.
An Orten, die nahezu dem kosmischen Beobachter gleichen – wie der Erdoberfläche –, ist damit die Rotationsgeschwindigkeit der Wirkungsquanten nahezu gleich der Lichtgeschwindigkeitskonstaten 0c – der Translationsgeschwindigkeit der Elapsonen-Strings. Dies ergibt sich aus Formel :
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {v_{wq}}\;\;\;=\;\;\;\sqrt{ {_{x,p}v_{wq,rot}^{2}} + {_{x,p}c^{2}} } } \] | () | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{x,p}v_{wq,rot}}\;\;\;=\;\;\;\sqrt{ {v_{wq}^2} - {_{x,p}c^{2}} } } \] | (ZAF.Wq.29) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}{_{0,p}v_{wq,rot}}\;\;\;=\;\;\;\sqrt{ (\sqrt{ 2 } \cdot {_{\raise -.3ex 0}c})^{2} - {_{\raise -.3ex 0}c}^{2} } } \] | (ZAF.Wq.30) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{0,p}v_{wq,rot}}\;\;\;=\;\;\;{_{\raise -.3ex 0}c} } \] | (ZAF.Wq.31) | ||
Danach stellt die Lichtgeschwindigkeitskonstante in der neuen Struktur des Bewegungsraums, also des Vakuums, in dreierlei Hinsicht etwas besonderes dar. Wobei die Wirkunsquanten-Geschwindigkeit das neue, an jedem Ort gültige Fixum verkörpert:
Ich folgere: Für einen trägt an seinem Ort nicht nur die Bewegung der Lichtteilchen – der Photonen – den Wert der Lichtgeschwindigkeitskonstanten(Verweis?), sondern auch deren Rotationsgeschwindigkeit. Weil die Lichtgeschwindigkeitskonstante auch noch in erhöhter Form in der Wirkunsquanten-Geschwindigkeit steckt, spielt diese eine Dreifachrolle. Wenn die Gravitation der Materie-Elementarteilchen der großen Massen des Kosmos ins Spiel kommt, fangen die beiden erstgenannten Varianten der Lichtgeschwindigkeit an sich entgegengesetzt zu entwickeln. Während sich die äußere Bewegung des Lichts im dreidimensionalen Raum nahe an den großen Massen verzögert, beschleunigt sich die Rotationsgeschwindigkeit dort und führt zu schnelleren Schwingungen der Elementarteilchen.
Konstant bleibt alleine die neue Wirkungsquanten-Geschwindigkeit, also die dritte, erhöhte Variante der Lichtgeschwindigkeit. Sie spielt so eine neue und zentrale Rolle.
In der heutigen Physik ist die gegensätzliche Doppelrolle der variablen Lichtgeschwindigkeit und der Drilling der Lichtgeschwindigkeit insgesamt, mit der Lichtgeschwindigkeitskonstanten im neuen Gewand der Wirkungsquanten-Geschwindigkeit, noch nicht erkannt. Dies ist einer der Gründe, warum die Lösung des ›Problems der Zeit‹ und damit die Vereinheitlichung der modernen Physik nicht gelingt. Die heutige Physik ordnet die Rotationsgeschwindigkeit über die innere Frequenz implizit der relativistischen Quantenfeldtheorie zu. Die Translationsgeschwindigkeit wird hingegen explizit der Allgemeinen Relativitätstheorie zugeordnet. Weil nur die Allgemeine Relativitätstheorie eine Aussage über die Veränderung der Lichtgeschwindigkeit im dreidimensionalen Raum macht, wird nur deren Aussage der Verringerung der Lichtgeschwindigkeit nahe großer Massen in Erwägung gezogen.
Stellt man sich nun mit den neuen Erkenntnissen im Hinterkopf vor, dass sich die beiden erstgenannten variablen Lichtgeschwindigkeiten aus Sicht der heutigen Physik bei steigender Gravitation nicht entgegengesesetzt verändern, wie in der Quanten-Fluss-Theorie, sondern wie heute angenommen beide verringern, die Frequenz sowie die Energie aber gleichzeitig ansteigen, so kann man nun durchschauen, warum man in der heutigen Physik zwangsläufig in der Sackgasse der Unendlichkeit landet.
| → |
|
| |
Dichtestruktur von Raum und Zeit |
|
Die Existenz Schwarzer Löcher und die fraktale Struktur des Universums
| ← |
|
Die nachfolgenden Erklärungen werden aus Sicht eines beschrieben.
Selbst ohne weiteres Wissen über den später entwickelten Mechanismus der Quantengravitation zu haben, ist es möglich, Informationen über fundamentale Eigenschaften des Bewegungsraums des Kosmos zu gewinnen. Aus den zuvor entwickelten, recht einfachen Formeln zur , und lässt sich ein Zusammenhang zwischen der relativen Wirkungsquanten-String-Dichte und der relativen Elapsonen-Bahn-Dichte im Kosmos herleiten. Aus diesem Zusammenhang, gemeinsam mit den im Kosmos, lässt sich die Erkenntnis gewinnen, dass der Kosmos Schwarze Löcher enthalten muss. Und es lässt sich darüber hinaus mit einiger Sicherheit erschließen, wie es in einem Schwarzen Loch aussieht: In einem Schwarzen Loch existiert ein Kosmos und dessen Urknall entspricht der Entstehung des Schwarzen Lochs. Folglich leben wir in einem fraktalen Universum.
Mit relativer Dichte ist eine bestimmte Dichte im Verhältnis zur im Kosmos gemeint. Diese durchschnittliche Dichte findet sich an allen Orten des B0.
Im Idealisierten Fall besteht der hier untersuchte Bewegungsraum des Vakuums des Kosmos aus kreisrunden, nicht elektromagnetisch polarisierten Wirkungsquanten-Strings, den Vakuum-Elapsonen. Die im Vakuum eingebetteten elektromagnetisch polarisierten Photonen und Elementarteilchen der Materie sind zum einen in ihrer Anzahl gegenüber den Vakuum-Elapsonen zu vernachlässigen und zum anderen tragen sie in Bezug auf die nachfolgend entwickelte Relation die gleichen entscheidenden Eigenschaften wie diese. Aus diesem Grund beschränke ich mich auf die Betrachtung der Elapsonen im Allgemeinen und meine damit vornehmlich die Vakuum-Elapsonen.
Relative Wirkungsquanten-String-Dichte oder -String-Energiedichte des Kosmos
Die Wirkungsquanten-Dichte ρep,wq eines Elapsonen-Strings, die Wirkungsquanten-String-Dichte, ergibt sich aus der Anzahl seiner Wirkungsquanten nep,wq im Verhältnis zur String-Länge uep: Die Anzahl an Wirkungsquanten eines Strings nep,wq ergibt sich nach Formel aus dem Verhältnis seiner Energie Eep zur Energie eines einzelnen Wirkungsquants Ewq. Das Ergebnis vereinfacht sich weiter, wenn man weiß, dass nach Formel die Energie jedes Wirkungsquants im Kosmos für einen bestimmten Beobachter überall gleich groß ist, weil Wirkungsquanten Energieeinheiten sind. Der Wechsel des Orts der Beaobachtung ergibt sich für die Energie nach Formel :
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {_{\raise -.3ex 0}\alpha}\;\;\;=\;\;\;1 } \] | () | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {_{x}n_{ep,wq}}\;\;\;=\;\;\;\frac{ {_{x}E_{ep}} }{ {_{x}E_{wq}} } } \] | () | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {_{x}E_{wq}}\;\;\;=\;\;\;{_{0}E_{wq}} } \] | () | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {_{y}E_{ep}}\;\;\;=\;\;\;{_{z}E_{ep}} \cdot \frac{ \sqrt{ 2 - {_{y}\alpha}^{2} } }{ \sqrt{ 2 - {_{z}\alpha}^{2} } } } \] | () | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {_{x}\rho_{ep,wq}}\;\;\;=\;\;\;\frac{ {_{x}n_{ep,wq}} }{ {u_{ep}} } } \] | (ZAF.RWD.1) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{x}\rho_{ep,wq}}\;\;\;=\;\;\;\frac{ \frac{ {_{x}E_{ep}} }{ {_{x}E_{wq}} } }{ {u_{ep}} } } \] | (ZAF.RWD.2) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{x}\rho_{ep,wq}}\;\;\;=\;\;\;\frac{ \frac{ {_{x}E_{ep}} }{ {_{0}E_{wq}} } }{ {u_{ep}} } } \] | (ZAF.RWD.3) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{x}\rho_{ep,wq}}\;\;\;=\;\;\;\frac{ {_{0}E_{ep}} \cdot \sqrt{ 2 - {_{x}\alpha}^{2} } }{ {_{0}E_{wq}} \cdot {u_{ep}} \cdot \sqrt{ 2 - {_{\raise -.3ex 0}\alpha}^{2} } } } \] | (ZAF.RWD.4) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{x}\rho_{ep,wq}}\;\;\;=\;\;\;\frac{ {_{0}E_{ep}} \cdot \sqrt{ 2 - {_{x}\alpha}^{2} } }{ {_{0}E_{wq}} \cdot {u_{ep}} } } \] | (ZAF.RWD.5) | ||
So lässt sich die Wirkungsquanten-Dichte eines Strings am Ort x durch seine Energie am Ort eines kosmischen Beobachters, den örtlichen Alterungsfaktor und seinen Umfang ausdrücken.
Die im Kosmos durchschnittliche Wirkungsquanten-Dichte eines Strings gewinnt man, indem man für diese Formel den Ort x = 0 des kosmischen Beobachters wählt:
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {_{\raise -.3ex 0}\rho_{ep,wq}}\;\;\;=\;\;\;\frac{ {_{0}E_{ep}} \cdot \sqrt{ 2 - {_{\raise -.3ex 0}\alpha}^{2} } }{ {_{0}E_{wq}} \cdot {u_{ep}} } } \] | (ZAF.RWD.6) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{\raise -.3ex 0}\rho_{ep,wq}}\;\;\;=\;\;\;\frac{ {_{0}E_{ep}} }{ {_{0}E_{wq}} \cdot {u_{ep}} } } \] | (ZAF.RWD.7) | ||
Die relative Wirkungsquanten-Dichte ist die Dichte im Verhältnis zum Durchschnitt:
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \frac{ {_{x}\rho_{ep,wq}}}{ {_{\raise -.3ex 0}\rho_{ep,wq}} }\;\;\;=\;\;\;}{ \frac{ \frac{ {_{0}E_{ep}} \cdot \sqrt{ 2 - {_{x}\alpha}^{2} } }{ {_{0}E_{wq}} \cdot {u_{ep}} } }{ \frac{ {_{0}E_{ep}} }{ {_{0}E_{wq}} \cdot {u_{ep}} } } } \] | (ZAF.RWD.8) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\frac{ {_{x}\rho_{ep,wq}}}{ {_{\raise -.3ex 0}\rho_{ep,wq}} }\;\;\;=\;\;\;\sqrt{ 2 - {_{x}\alpha}^{2} } } \] | (ZAF.RWD.9) | ||
Schlussfolgerung: Die relative Wirkungsquanten-String-Dichte eines Eleapsonen-Strings ist für alle Strings an einem bestimmten Ort gleich und hängt ausschließlich vom Alterungsfaktor des betrachteten Orts ab. Berechnet man die relative Wirkungsquanten-Dichte für einen , und nicht nur für den kosmischen, dann kommt man auf das selbe Ergebnis. Diese Eigenschaft des Bewegungsraums ist also auch Beobachter unabhängig. Mit seiner Hilfe lässt sich also eine allgemeine Aussage über diese Eigenschaft eines Orts des Bewegungsraums machen. Diese Eigenschaft ist die relative Energiedichte der Strings des Bewegungsraums, weil jedes Wirkungsquant einer Energieeinheit entspricht.
Relative Elapsonen-Bahn-Dichte oder Elementarteilchen-Liniendichte des Kosmos
Um die relative Elapsonen-Dichte entlang ihrer Bewegungsbahn, die Elapsonen-Bahn-Dichte, zu berechnen, beginnt man mit der Berechnung der absoluten Elapsonen-Dichte auf einer Wegstrecke. Die Dichte ergibt sich dabei aus der Anzahl der Elapsonen nep pro Wegstrecke wep. Die Elapsonen bewegen sich mit der ortsüblichen Lichtgeschwindigkeit xc im dreidimensionalen Raum, die sich nach Formel proportional zum absoluten Alterungsfaktor ⍺ verändert. Deshalb stauen sich die hintereinanderher laufenden Elapsonen bei Verlangsamung umgekehrt proportional zum abnehmenden Alterungsfaktor auf, weil ihre Detektorwellenlänger λep,d sich entsprechend verringert (siehe ). Dadurch sind auf der Wegstrecke umgekehrt proportional zum absoluten Alterungsfaktor mehr Elapsonen zu finden, als beim kosmischen Beobachter: (Die Detektorwellenlängenveränderung der Elapsonen nach , verschieben und hier dort hin verweisen (siehe ).)
So lässt sich die absolute Dichte der Elapsonen auf ihrer Bewegungsbahn im Kosmos einfach ausdrücken.
Auf die absolute Dichter der Elapsonen auf ihrer Bewegungsbahn im kosmischen Druchschnitt kommt man dann, wenn man am Ort des kosmichen Beobachters B0 schaut:
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {_{\raise -.3ex 0}\alpha}\;\;\;=\;\;\;1 } \] | () | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {_{\raise -.3ex 0}\rho_{ep}}\;\;\;=\;\;\;\frac{ _{\raise -.3ex 0}{n_{ep}} }{ {w_{ep}} \cdot {_{\raise -.3ex 0}\alpha} } } \] | (ZAF.RED.4) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{\raise -.3ex 0}\rho_{ep}}\;\;\;=\;\;\;\frac{ _{\raise -.3ex 0}{n_{ep}} }{ {w_{ep}} } } \] | (ZAF.RED.5) | ||
Die relative Elapsonen-Bahn-Dichte ist die Dichte im Verhältnis zum Durchschnitt:
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \frac{ {_{x}\rho_{ep}}}{ {_{\raise -.3ex 0}\rho_{ep}} }\;\;\;=\;\;\;\frac{ \frac{ _{\raise -.3ex 0}{n_{ep}} }{ {w_{ep}} \cdot {_{x}\alpha}} }{ \frac{ _{\raise -.3ex 0}{n_{ep}} }{ {w_{ep}} } } } \] | (ZAF.RED.6) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\frac{ {_{x}\rho_{ep}}}{ {_{\raise -.3ex 0}\rho_{ep}} }\;\;\;=\;\;\;\frac{ 1 }{ {_{x}\alpha} } } \] | (ZAF.RED.7) | ||
Auch die relative Elapsonen-Bahn-Dichte ist also ausschließlich vom Alterungsfaktor abhängig.
Schlussfolgerung: Hier gilt im Prinzip eine analoge Schlussfolgerung zu der der .
|
Relation von Wirkungsquanten-String-Dichte und Elapsonen-Bahn-Dichte im Kosmos
Um die Relation der Wirkungsquanten-String- und Elapsonen-Bahn-Dichte zu berechnen lässt sich ausnutzen, dass beide relativen Dichten ausschließlich vom Alterungsfaktor abhängig sind. So kann man beide nach dem Alterungsfaktor ⍺ umstellen und gleichsetzen.
Für die relative Wirkungsquanten-String-Dichte ergibt sich dann:
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \frac{ {_{x}\rho_{ep,wq}}}{ {_{\raise -.3ex 0}\rho_{ep,wq}} }\;\;\;=\;\;\;\sqrt{ 2 - {_{x}\alpha}^{2} } } \] | () | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\Bigl( \frac{ {_{x}\rho_{ep,wq}}}{ {_{\raise -.3ex 0}\rho_{ep,wq}} } \Bigr)^{2}\;\;\;=\;\;\;2 - {_{x}\alpha}^{2} } \] | (ZAF.RWE.1) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\Bigl( \frac{ {_{x}\rho_{ep,wq}}}{ {_{\raise -.3ex 0}\rho_{ep,wq}} } \Bigr)^{2} + {_{x}\alpha}^{2}\;\;\;=\;\;\;2 } \] | (ZAF.RWE.2) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{x}\alpha}^{2}\;\;\;=\;\;\;2 - \Bigl( \frac{ {_{x}\rho_{ep,wq}}}{ {_{\raise -.3ex 0}\rho_{ep,wq}} } \Bigr)^{2} } \] | (ZAF.RWE.3) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{x}\alpha}\;\;\;=\;\;\;\sqrt{ 2 - \Bigl( \frac{ {_{x}\rho_{ep,wq}}}{ {_{\raise -.3ex 0}\rho_{ep,wq}} } \Bigr)^{2} } } \] | (ZAF.RWE.4) | ||
Für die relative Elapsonen-Bahn-Dichte ergibt sich dann:
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \frac{ {_{x}\rho_{ep}}}{ {_{\raise -.3ex 0}\rho_{ep}} }\;\;\;=\;\;\;\frac{ 1 }{ {_{x}\alpha} } } \] | () | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{x}\alpha}\;\;\;=\;\;\;\frac{ 1 }{ \frac{ {_{x}\rho_{ep}}}{ {_{\raise -.3ex 0}\rho_{ep}} } } } \] | (ZAF.RWE.5) | ||
Setzt man beide Dichteformeln gleich und stellt die Gleichung nach der Elapsonen-Bahn-Dichte um, erhält man die Relation:
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \frac{ 1 }{ \frac{ {_{x}\rho_{ep}}}{ {_{\raise -.3ex 0}\rho_{ep}} } }\;\;\;=\;\;\;\sqrt{ 2 - \Bigl( \frac{ {_{x}\rho_{ep,wq}}}{ {_{\raise -.3ex 0}\rho_{ep,wq}} } \Bigr)^{2} } } \] | (ZAF.RWE.6) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\frac{ {_{x}\rho_{ep}}}{ {_{\raise -.3ex 0}\rho_{ep}} }\;\;\;=\;\;\;\frac{ 1 }{ \sqrt{ 2 - \Bigl( \frac{ {_{x}\rho_{ep,wq}}}{ {_{\raise -.3ex 0}\rho_{ep,wq}} } \Bigr)^{2} } } } \] | (ZAF.RWE.7) | ||
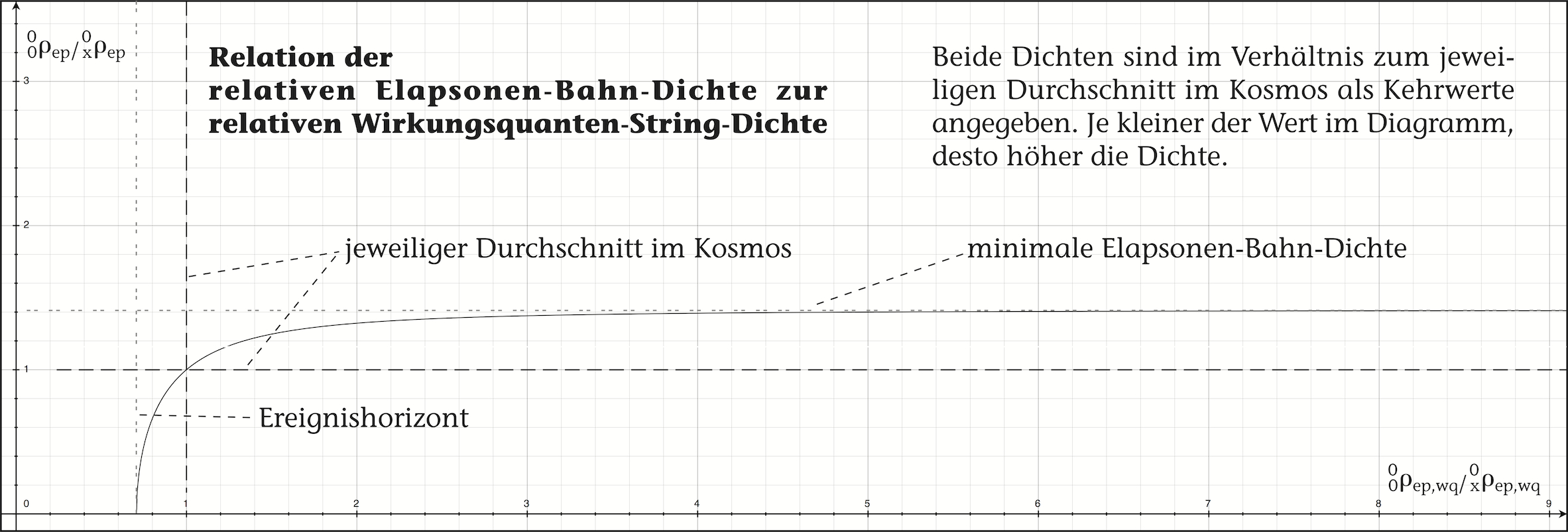
Die stellt die Relation in Form der Kehrwerte der Dichten dar; zum einen, damit sich die interessanten Zusammanhänge nicht im Unendlichen abspielen; und zum anderen, weil die Verhältnisse auf diese Weise eher denen einer Zentralmasse entsprechen. Denn der Kehrwert der Elapsonen-Bahn-Dichte ist nach Formel dem absoluten Alterungsfaktor x⍺ gleich, der zu einer Masse hin bei steigender Gravitation abnimmt, bis er am Ereignishorizont zu Null wird. Eine gedachte Zentralmasse würde sich im Diagramm im Nullpunkt befinden.
Doch wie ist das Diagramm nun zu interpretieren? Das Diagramm zeigt, dass zur Zentralmasse hin nicht nur die Elapsonen-Bahn-Dichte, sondern auch die Wirkungsquanten-String-Dichte im Bewegungsraum, also letztendlich im Vakuum, ansteigt.
Interpretation: Denkt man sich die Zentralmasse mal so klein, wie möglich. Während die Wirkungsquanten-String-Dichte zum Zentrum hin beständig weiter zunimmt, gilt dies für die Dichte der Elapsonen entlang ihrer Bewegungsbahn auch. Aber an der Stelle √0,5 geht die Elapsonen-Dichte plötzlich gegen unendlich; im Diagramm fällt die Kurve auf Null herunter.
Die Quanten-Fluss-Theorie unterstellt eine endliche Anzahl an Wirkungquanten und Elapsonen in einem endlichen Volumen.(Diese Definition in die Einführung? Sie kann auch lauten, dass der Kosmos nur endlich viele WQ und vEp enthält.) Dann kann es nirgendwo eine wirklich unendliche Dichte an Elapsonen geben. Doch was passiert dann an dieser Stelle?
Die entwickelten Formeln der Helixspiralbahn der Wirkungsquanten in einem Elapsonen-String verlieren ihre Gültigkeit, sobald sich der String auflöst und damit die Wirkungsquanten-Bahn ihre Helixform verliert. Ich nehme an, dass genau dies an dieser Stelle passiert. Unterhalb von √0,5 gibt es dann auf der gleichen Ebene keine Wirkungsquanten-Strings mehr, wie oberhalb. Es gibt nur noch freie Wirkungsquanten, die nach dem fraktalen Existenzprinzip dann Mikro-Wirkungsquanten-Strings sind. Doch dies bedeutet eine Verletzung der Wirkungsquanten-String-Anzahlerhaltung. (Die Verletzung der Wirkungsquanten-String-Anzahlerhaltung muss es nicht geben, wenn bei der Entstehung des Schwarzen Lochs alle Wirkungsquanten-Strings, die zuvor in der urpsrünglichen Masse vorhanden waren, am Ereignishorizont verbleiben. Im Schwarzen Loch wären dann nur Wirkungsquanten, die sich auch zuvor schon frei zwischen den Strings bewegt haben.)
Danach ist diese Stelle ein Übergangspunkt von einer Fraktal-Ebene des Universums auf eine andere; ein Phasenübergang. Da dieser Übergang für eine Annäherung aus jeder Richtung auf die Zentralmasse gilt handelt es sich in Wirklichkeit um eine kugelförmige Übergangsfläche. Und diese Übergangsfläche hat etwas mit den Schwarzen Löchern der Allgemeinen Relativitätstheorie gemein: Weil der absolute Alterungsfaktor x⍺ gegen Null geht, kommt dort die Lichtgeschwindigkeit im dreidimensionalen Raum im Prinzip zum Stehen, genau so, als wenn man sich einem Ereignishorizont, eines Schwarzen Lochs nähern würde. Die Verletzung der Wirkungsquanten-String-Anzahlerhaltung wäre folglich nach außen hin durch eine Art Übergangshorizont abgeschirmt.
Ich schließe also, die Relation von Wirkungsquanten-String- und Elapsonen-Bahn-Dichte zeigt zusammen mit den Erhaltungssätzen des Bewegungsraums die Existenz Schwarzer Löcher im Kosmos und offenbart die fraktale Struktur des Universums.
Relative Wirkungsquanten- oder Vakuum-Energie-Dichte im Kosmos
In Planung …
| → |
|
| |
Formeln des Bewegungsraums |
|
Die allgemeine, ergänzende Formelsammlung
| ← |
|
Beobachter- und Beobachtungsortswechsel
Bisher wurden beobachtete Veränderungen – hier Prozesse genannt, wie Bewegungen oder Schwingungen – überwiegend aus der Perspektive eines im Kosmos ruhenden beschrieben. Für einen solchen Beobachter laufen Zeit und Alterung gleich, wie im Kapitel schon gezeigt wurde:
Weil es nun komplexer wird, wurde ein für den Ort eingeführt, von dem aus beobachtet wird.
In diesem Fall eine 0 für eine Beobachtung aus Sicht des kosmischen Beobachters B0, der von Orten mit im Kosmos durchschnittlicher Wirkungsquanten- und Elapsonen-Dichte aus beobachtet.
Für die Änderung der Alterung im dreidimensionalen Raum ergab sich dann die Formel :
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{^{0}_{x}a}\;\;\;=\;\;\;{^{0}_{0}a} \cdot {^{0}_{x}\alpha} } \] | () |
Der Alterungsfaktor ⍺ aus Sicht des kosmsichen Beobachters ist als zum Kosmos absolut zu bezeichnen.
Der relative Alterungsfaktor zwischen zwei beliebigen Orten x und y entspricht dem Verhältnis der absoluten Alterungen beider Orte:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {^{y}_{x}\alpha}\;\;\;=\;\;\;\frac{ {^{0}_{x}a} }{ {^{0}_{y}a} } } \] | (ZAF.Bw.1) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{^{y}_{x}\alpha}\;\;\;=\;\;\;}{ \frac{ {^{0}_{0}a} \cdot {^{0}_{x}\alpha} }{ {^{0}_{0}a} \cdot {^{0}_{y}\alpha} } } \] | (ZAF.Bw.2) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{^{y}_{x}\alpha}\;\;\;=\;\;\;\frac{ {^{0}_{x}\alpha} }{ {^{0}_{y}\alpha} } } \] | (ZAF.Bw.3) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{^{0}_{x}\alpha}\;\;\;=\;\;\;{^{0}_{y}\alpha} \cdot {^{y}_{x}\alpha} } \] | (ZAF.Bw.4) | ||
So stehen auch die beiden absoluten Alterungsfaktoren zweier Orte über den relativen Alterungsfaktor im Zusammenhang.
Das Verhältnis bleibt das gleiche, wenn man von einem Ort z die Orte y und x beobachtet. Also ergibt sich für die Alterung und die Lichtgeschwindigkeit allgemeiner:
Der Wechsel des Beobachtungsorts von Alterung ist somit recht simpel beschrieben.
Etwas komplexer sieht es aus, wenn die Schwingungen von Elemeantarteilchen und die mit ihnen verknupften Eigenschaften, wie Frequenz, Energie, Impuls und Masse, an unterschiedlichen Orten im Bewegungsraum beobachtet werden. Alle genannten Größen ändern sich proportional mit der Frequenz (siehe Formel (weitere Formeln)). Wenn man berücksichtigt, dass der vom bereinigte Umfang uph sich nicht verändert, kann man für das Verhältnis der Frequenzänderung sagen:
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {_{x}f_{ph}}\;\;\;=\;\;\;\sqrt{ 2 - {_{x}\alpha}^{2} } \cdot \frac{ {_{\raise -.3ex 0}c} }{ {_{x}u_{ph}} } } \] | () | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \frac{ {_{y}f_{ph}} }{ {_{z}f_{ph}} }\;\;\;=\;\;\;}{ \frac{ \sqrt{ 2 - {_{y}\alpha}^{2} } \cdot \frac{ {_{\raise -.3ex 0}c} }{ {_{y}u_{ph}} } }{ \sqrt{ 2 - {_{z}\alpha}^{2} } \cdot \frac{ {_{\raise -.3ex 0}c} }{ {_{z}u_{ph}} } } } \] | (ZAF.Bw.8) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\frac{ {_{y}f_{ph}} }{ {_{z}f_{ph}} }\;\;\;=\;\;\;\frac{ \sqrt{ 2 - {_{y}\alpha}^{2} } }{ \sqrt{ 2 - {_{z}\alpha}^{2} } } } \] | (ZAF.Bw.9) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{y}f_{ph}}\;\;\;=\;\;\;{_{z}f_{ph}} \cdot \frac{ \sqrt{ 2 - {_{y}\alpha}^{2} } }{ \sqrt{ 2 - {_{z}\alpha}^{2} } } } \] | (ZAF.Bw.10) | ||
Das selbe Verhältnis ergibt sich auch für die Veränderung von Energie, Impuls und Masse:
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {_{x}E}\;\;\;=\;\;\;{_{x}f} \cdot h } \] | () | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}{_{y}f_{ph}} \cdot h\;\;\;=\;\;\;{_{z}f_{ph}} \cdot h \cdot \frac{ \sqrt{ 2 - {_{y}\alpha}^{2} } }{ \sqrt{ 2 - {_{z}\alpha}^{2} } } } \] | (ZAF.Bw.11) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{y}E_{ph}}\;\;\;=\;\;\;{_{z}E_{ph}} \cdot \frac{ \sqrt{ 2 - {_{y}\alpha}^{2} } }{ \sqrt{ 2 - {_{z}\alpha}^{2} } } } \] | (ZAF.Bw.12) | ||
Die Wahrnehmung eines beliebigen Beobachters eines jeden Veränderungsprozesses, egal ob Bewegung oder Schwingung, irgendwo im Kosmos ist von seiner eigenen Alterung abhängig. Diese Prozesse erscheinen ihm umgekehrt proportional zu seinem eigenen Alterungsfaktor im Kosmos. Altert er am Ort y mit ⍺ langsamer, läuft jeder von ihm am Ort x beobachtete Prozess apc umso schneller ab:
Mit einem Prozess ist dabei jede Art der Veränderung gemeint, jede Bewegung, also selbst die Bewegung der Wirkungsquanten.
So ergibt sich für einen beliebigen Prozess am Ort x, der zuvor vom Ort z aus und nun von y aus beobachtet wird, unter Benutzung von Formel :
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}{^{0}_{x}a_{pc}}\;\;\;=\;\;\;{^{0}_{x}a_{pc}} } \] | (ZAF.Bw.15) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{^{y}_{x}a_{pc}} \cdot {^{0}_{y}\alpha}\;\;\;=\;\;\;{^{z}_{x}a_{pc}} \cdot {^{0}_{z}\alpha} } \] | (ZAF.Bw.16) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{^{y}_{x}a_{pc}}\;\;\;=\;\;\;{^{z}_{x}a_{pc}} \cdot \frac{ {^{0}_{z}\alpha} }{ {^{0}_{y}\alpha} } } \] | (ZAF.Bw.17) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{^{y}_{x}a_{pc}}\;\;\;=\;\;\;{^{z}_{x}a_{pc}} \cdot {^{y}_{z}\alpha} } \] | (ZAF.Bw.18) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{^{y}_{x}a_{pc}}\;\;\;=\;\;\;\frac{ {^{z}_{x}a_{pc}} }{ {^{z}_{y}\alpha} } } \] | (ZAF.Bw.19) | ||
Der Beobachterwechsel für Prozesse ist also recht simpel zu beschreiben.
Wirkungsquanten-Strings
Für alle Wirkunsgquanten-Strings gilt, dass die Gesamtenergie eines Elementarteilchen-Strings Eele die Summe der Energie Ewq all seiner nele,wq Wirkungsquanten ist (siehe Formel FP.1). Dabei ist die Energie jedes Wirkungsquants Ewq für den selben Beaobachter überall gleich groß, weil es sich um Energieeinheiten handelt. Für unterschiedliche Beobachter können die Energieeinheiten allerdings unterschiedlich groß sein. Deshlab nehmen alle Beobachter die gleiche Anzahl an Wirkungsquanten in einem Elementarteilchen wahr, dass sich am selben Ort befindet:
Die Wirkungsquanten-Anzahl ergibt sich also aus dem Verhältnis seiner Energie zur Energie eines Wirkungsquants.
Wegen der Einsteinschen Energie-Masse-Äquivalenz gilt äquivalentes auch für die Masse (siehe Formel FP.2).
(Die Detektorwellenlängenveränderung der Elapsonen aus , ZAF.RED.1, hier entwickeln und von dort hierher verweisen.)
| → |
|
| |
Definition von Subräumen |
|
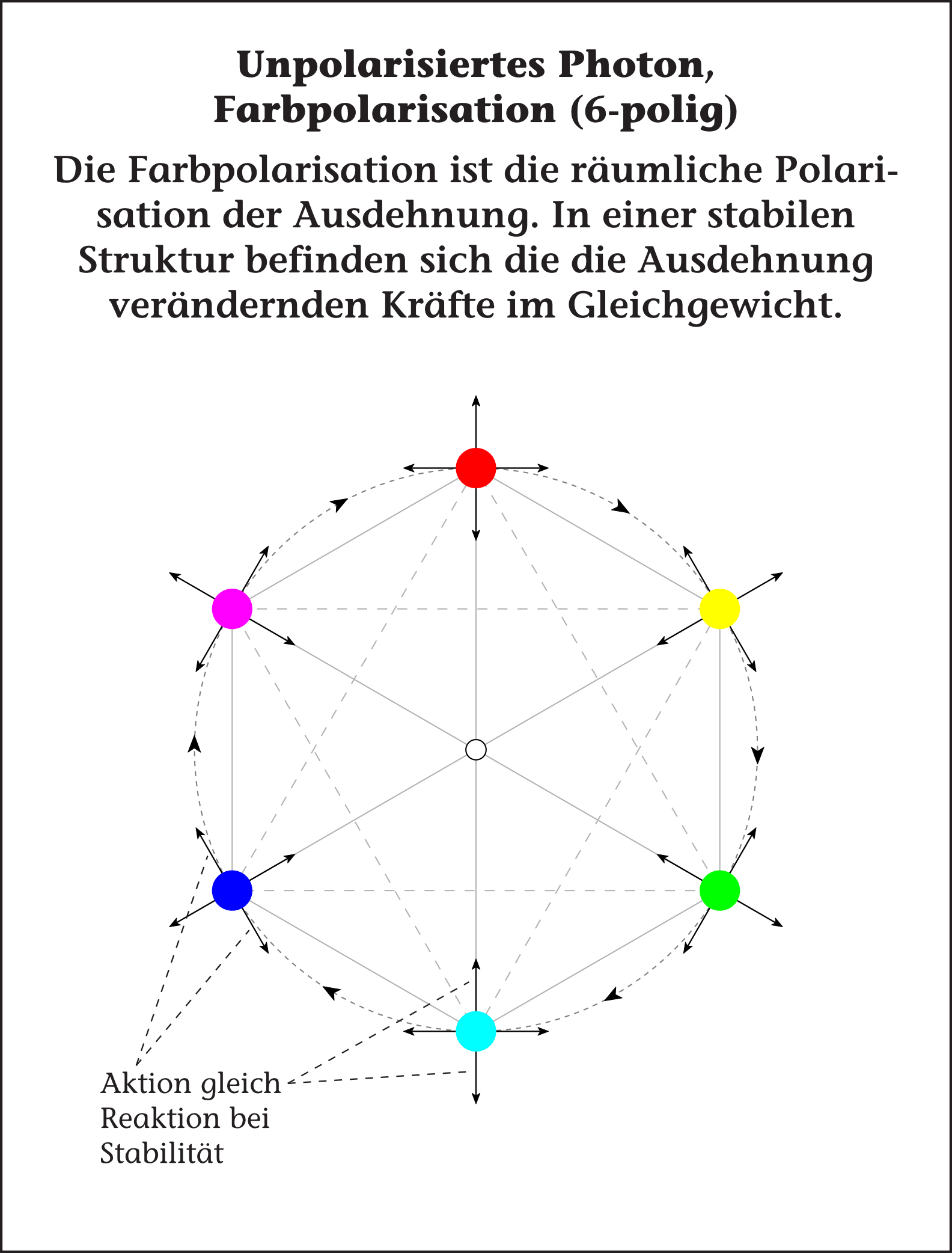
Farbpolarisation ist Raumrichtungspolarisation
| ← |
|
|
Sollen strukturierte Dinge in einem Raum existieren, dann müssen diese vom Rest räumlich abgegrenzt sein. Wir kommen nicht darum herum, sie in einem Subraum zu verorten.
Zur Definition eines n-dimensionalen Subraums in einem n-dimensionalen Raum werden immer mindestens n+1 Punkte benötigt:
| • |
In einem Punkt, also in null Dimensionen, kann genau ein Punkt definiert werden. Sein Gegenpol fällt mit diesem zusammen. |
| • |
Auf einer Gerade, in einem eindimensionalen Raum, werden mindestens zwei Punkte benötigt, um eine Linie zu definieren. Die Gegenpole der Linienendpunkte fallen genau mit dem jeweils anderen Endpunkt zusammen. |
| • |
Auf einer Fläche, in einem zweidimensionalen Raum, werden mindestens drei Punkte benötigt, um eine Teilfläche zu definieren. Die Gegenpunkte liegen jeweils zwischen den anderen beiden Punkten. Zusammen sind es sechs, die ein Hexagramm ergeben. |
| • |
In einem dreidimensionalen Raum werden mindestens vier Punkte benötigt, um einen Unterraum oder Subraum zu definieren. Die Gegenpunkte liegen immer zwischen den anderen drei Punkten. Es ergeben sich gemeinsam acht Punkte. |
So erklärt sich, warum auf einem Kreis mindestens drei Farben zum Mischen nötig sind, damit sich die Mischfarben auf dem Farbkreis nicht wiederholen. Auf einer Farbkugel sind daher vier Farben notwendig, dies zu erreichen.
Dies erklärt die Darstellung der Farbpolarisation der Quantenchromodynamik mit drei (siehe ) oder vier Grundfarben und deren Komplementärfarben. In der Quanten-Fluss-Theorie ist dies die Raumrichtungspolarisation.
Ein Prisma
Wie kommt es, dass die Raumrichtungspolarisation so gut zum Farbspektrum passt?
Ein Hinweis auf die Antwort auf die Frage liegt in einem Prisma:
Weißes Licht lässt sich durch ein Prisma in sein Farbspektrum zerlegen, welches nach seiner Farbe und Frequenz in unterschiedliche Raumrichtungen aufgefächert wird. Die Analogie ist so gesehen tatsächlich frappierend.
Entsprechend gilt für jedes Elementarteilchen, dass es umso kleiner ist, je höher seine Frequenz. Auch hier hängt die Raumrichtungspolarisation von der Frequenz ab.
Es ist also interessant, sich darum Gedanken zu machen, wie weit diese Zusammenhänge miteinander Verbunden werden können. Dichten von Medien könnten hier, nach meiner Intuition, eine Rolle spielen.
Besonderheit
Hier drinne steckt bemerkenswerterweise das Zählen, weil Subräume einer Dimension immer mindestens einen Punkt mehr zur Definition benötigen, als die Dimensionszahl selber, von der sie einen Teil mit der gleichen Dimensionszahl abgrenzen. Im inneren, in der Abgrenzung eines Teils, steckt also auf eine gewisse Weise mehr, als der Aufwand, diesen Raum der Möglichkeiten zur Verfügung zu stellen.
Dies hat Ähnlichkeiten mit den Bits: Stellen wir acht Bits zur Verfügung, die ja jeweils Null oder Eins sein können, so ergeben sich 256 Möglichkeiten, diese zu setzen, sie zu variieren.
| → |
|
| |
Holografisches Prinzip |
|
Subräume, ihr Informationsgehalt und ihr Informationsaustausch
| ← |
|
Beim Holographischen Prinzip geht es um das Verhältnis der Informationsmenge, die durch die Kugeloberfläche eines Subraumes von innen nach außen fließen kann, im Verhältnis zum Informationsgehalt seines sphärischen Volumens.
Das ist dabei durch die vorstehend beschriebene Raumrichtungspolarisation seiner Struktur gegeben, durch seine Farbpolarisation.
Verhältnis der Kombinationsmöglichkeiten des Kugelinneren zu seiner Oberfläche
Der Informationsfluss durch die Kugeloberfläche eines Subraums kann durch hypothetische Pixel, gleich großer Teilflächen, seiner Oberfläche beschrieben werden. Jeder Pixel fungiert hierbei als Bit, das Null oder Eins sein kann. Die maximale Informationsmenge seiner Oberfläche ist das, was maximal in einem Moment durch sie hindurch fließen und so nach außen dringen kann. Sie entspricht der maximalen Kombinationsmöglichkeit seiner Oberflächen-Pixel.
Der theoretisch maximale Informationsgehalt des Kugelvolumens entspricht den maximalen Kombinationsmöglichkeiten seiner Voxel, gleich großer Teilvolumen in ihm, die den Kantenlänge der Pixeln seiner Oberfläche gleichen. Auch hier kann nach dem Holographischen Prinzip kombinatorisch jedes Voxel wie ein Bit nur Null oder Eins sein.
Unter freien Bedingungen ist bei Volumen, die deutlich größer als ein Voxel sind, die Kombinationsanzahl des Volumens deutlich größer, als die Kombinationsanzahl der Oberfläche. XXX XXX XXX XXX XXX
Voxel stehen miteinander in einem Zusammenhang
Das Holographische Prinzip besagt nun, dass die Kombinationsmöglichkeit der Voxel in einem festen Verhältnis zu denen der Pixel steht. Beide sind Proportional zu einander.
Dies lässt sich so interpretieren, dass der Informationsgehalt der Voxel nicht größer sein kann, als der Informationsgehalt, der durch die Pixel der sie umschließenden Kugeloberfläche nach außen transportiert werden kann.
Mit noch anderen Worten sind die Bits der Voxel nicht frei kombinierbar, sondern nur in dem Maß, wie die Bits seiner Oberfläche multipliziert mit einer Konstanten. Die Voxel im Inneren der Kugel stehen also miteinander in einem Zusammenhang, der umso größer wird, je mehr Voxel das Volumen enthält. XXX XXX XXX XXX XXX XXX
Der Informationsfluss zwischen zwei Subräumen bringt diese in eine Abhängigkeit
Der Informationsfluss zwischen zwei Subräumen bringt diese in einen Zusammenhang. Sie können sich nicht mehr unabhängig voneinander verändern, also entwickeln, weil sie miteinander in einer Rückkopplung kommunizieren.
Dies wird auch dadurch deutlich, dass die sie beide zusammen umgebende Kugel im Verhältnis zu ihren Voxeln viel weniger Pixel auf ihrer Oberfläche besitzt, als dies bei den beiden in ihr enthaltenen Subräumen der Fall war. XXX XXX XXX XXX XXX
| → |
| |
Fußnoten |
|
| 1. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Quantenfeldtheorie. | |
| 2. |
Vgl. Fließbach, Allgemeine Relativitätstheorie. Vgl. Harrison, Kosmologie, Kap. 8 Allgemeine Relativitätstheorie, S. 253-290. Vgl. Born, Die Relativitätstheorie Einsteins, Kap. VII. Die allgemeine Relativitätstheorie Einsteins, S. 266-324. Vgl. Einstein, »Die Grundlagen der allgemeinen Relativitätstheorie«. Internet: Vgl. Wikipedia, Allgemeine Relativitätstheorie. | |
| 3. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Allgemeine Relativitätstheorie, Grundlegende Konzepte, Raumzeitkrümmung. | |
| 4. |
Internationaler Standard: Vgl. NIST, CODATA Value: speed of light in vacuum. Internet: Wiki einpflegen. | |
| 5. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Energieerhaltungssatz. | |
| 6. |
(Primärliteratur einfügen!) Vgl. Marinoni, »A geometric measure of dark energy with pairs of galaxies«. Vgl. Lesch, Kosmologie für helle Köpfe, hier S. 144, 201. Sekundärliteratur: Vgl. Börner, »Die Dunkle Energie und ihre Feinde«, hier S. 41-42. Vgl. Freedman, »Das Expandierende Universum«. Internet: (Internetliteratur einfügen!) | |
| 7. |
Internationaler Standard: Vgl. NIST, CODATA Value: speed of light in vacuum. Internet: Wiki einpflegen. | |
| 8. |
Vgl. Shapiro, »Fourth Test of General Relativity«. Internet: Vgl. Wikipedia, Shapiro-Verzögerung. | |
| 9. |
Vgl. Schwarzschild, Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie. Internet: Vgl. Wikipedia, Schwarzschild-Metrik. | |
| 10. |
Vgl. Giese, The Origin of Gravity, Kap. 2 Bending of a Beam of Light Passing a Massive Object, S. 1-4, hier Formel 2.1, S. 1. Diese Formel kann man aus der Veränderung der Detektorwellenlänge der Schwarzschild-Lösung herleiten: Vgl. Harrison, Kosmologie, Kap. 9 Schwarze Löcher, S. 291-323, hier S. 295, ergänzendes S. 297, 320. Internet: Vgl. Wikipedia, Gravitational redshift, Definition. | |
| 11. | Wie der Richtungsparameter zu verstehen ist wird im Kapitel Lichtverlangsamung beschrieben. | |
| 12. | Vgl. Giulini, Gravitation, Equivalence Principle, and Quantum Mechanics, S. 13-14. | |
| 13. |
Vgl. Fließbach, Allgemeine Relativitätstheorie, Teil III Physikalische Grundlagen der ART, Kap. 12 Gravitationsrotverschiebung, S. 58-64. Vgl. Vessot, »Test of Relativistic Gravitation with Maser«. Vgl. Pound, »Effect of Gravity on Gamma Radiation«. Internet: Vgl. Wikipedia, Pound-Rebka-Experiment. | |
| 14. | Vgl. Pound, »Effect of Gravity on Gamma Radiation«, Intruduction, S. B 788. | |
| 15. | Dies ist mit Sicherheit richtig. Ich meine ich hatte dies vor Jahren irgendwo gelesen und daher übernommen. Leider konnte ich es bisher nicht wieder finden oder ersehen, woher ich es abgeleitet hatte. Dies ist also heraus zu finden. Alternativ zeigen, dass die Steigung der Formel $ \frac{ g \cdot h }{ c^{2} } $ aus dem Pound-Rebka-Snider-Experiment entsprechend passt. Beziehungsweise $ \frac{ \Delta \nu }{ \nu_{0} } = - \frac{ \Delta \phi_{g} }{ c^{2} } $ , vgl. Pound, »Effect of Gravity on Gamma Radiation«, S. B 788. | |
| 16. | Dies ist mit Sicherheit richtig. Ich meine ich hatte dies vor Jahren irgendwo gelesen und daher übernommen. Leider konnte ich es bisher nicht wieder finden oder ersehen, woher ich es abgeleitet hatte. Dies ist also heraus zu finden. Alternativ zeigen, dass die Steigung der Formel $ \frac{ g \cdot h }{ c^{2} } $ aus dem Pound-Rebka-Snider-Experiment entsprechend passt. Beziehungsweise $ \frac{ \Delta \nu }{ \nu_{0} } = - \frac{ \Delta \phi_{g} }{ c^{2} } $ , vgl. Pound, »Effect of Gravity on Gamma Radiation«, S. B 788. | |
| 17. |
Vgl. Harrison, Kosmologie, Kap. 9 Schwarze Löcher, S. 291-323. Internet: Vgl. Wikipedia, Schwarzes Loch. | |
| 18. |
(Primärliteratur einfügen!) Vgl. Harrison, Kosmologie, Kap. 9 Schwarze Löcher, S. 291-323, hier S. 301-322. Internet: Vgl. Wikipedia, Ereignishorizont. | |
| 19. | Es handelt sich im Fall der Quanten-Fluss-Theorie nicht wirklich um einen Ereignishorizont im Sinne der Allgemeinen Relativitätstheorie. Wie genau sich die Dinge dort Verhalten, wo sich die Elapsonen stauen, ist zu untersuchen. Klar scheint, dass in dieser Theorie von außen betrachtet kein Elementarteilchen unzerstört durch den Übergangshorizont gehen kann. Dann ist dies auch aus Sicht des Elementarteilchens nicht möglich. (Literatur: Artikel GEO 10/2014, "Wie schwarz ist Schwarz?", S. 130–144.) (Thema auf die Diskussionsseite aufnehmen.) |
| |
Stand 20. November 2025, 23:00 CET.
-
Permanente Links:
(Klicke auf die Archivlogos
zum Abruf und Ansehen
der Archive dieser Seite.) -

-
archive.todaywebpage capture