| ← |
Elementarteilchenmodell mit Wirkungsquanten-Strings
Schwärme von Wirkungsquanten fügen sich zu Wirkungsquanten-Strings zusammen
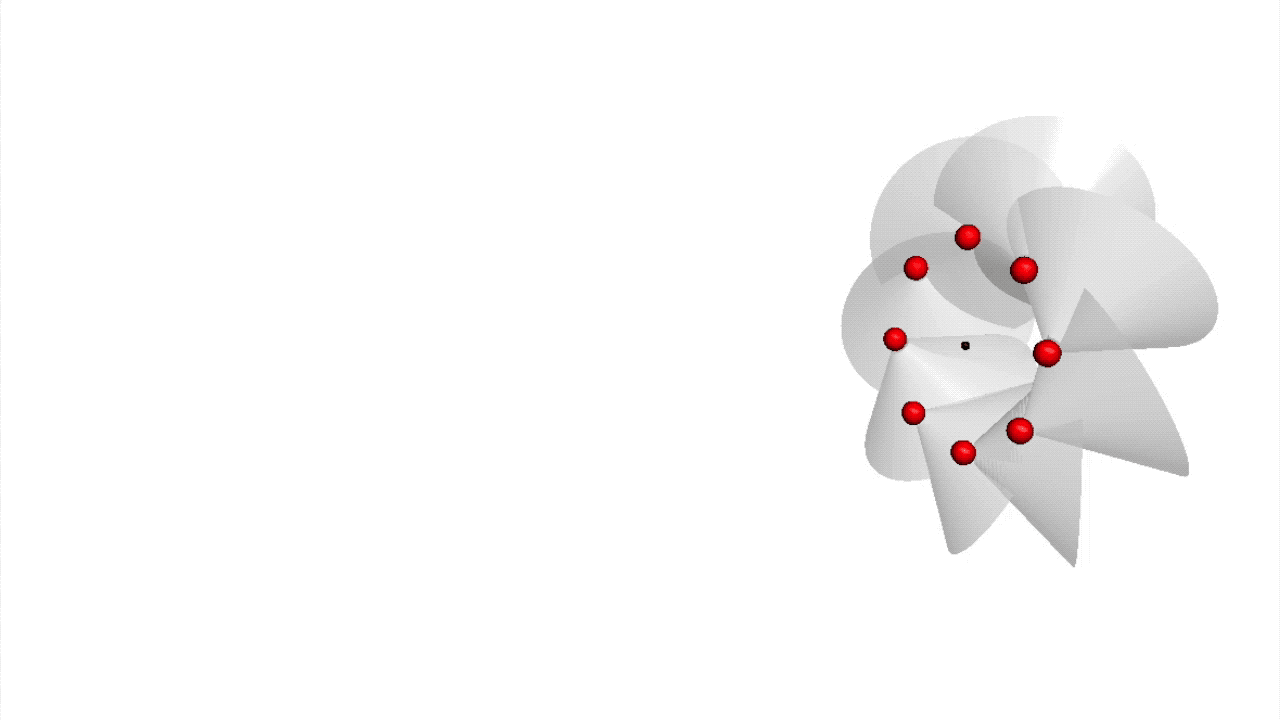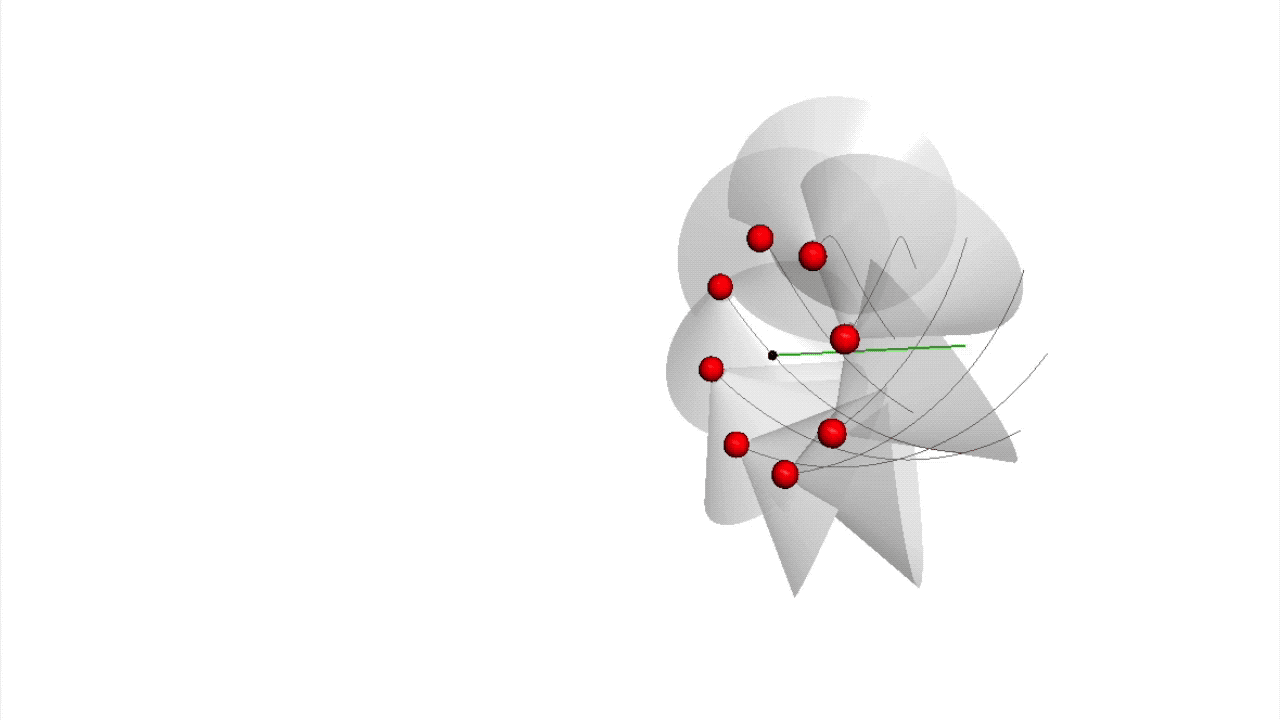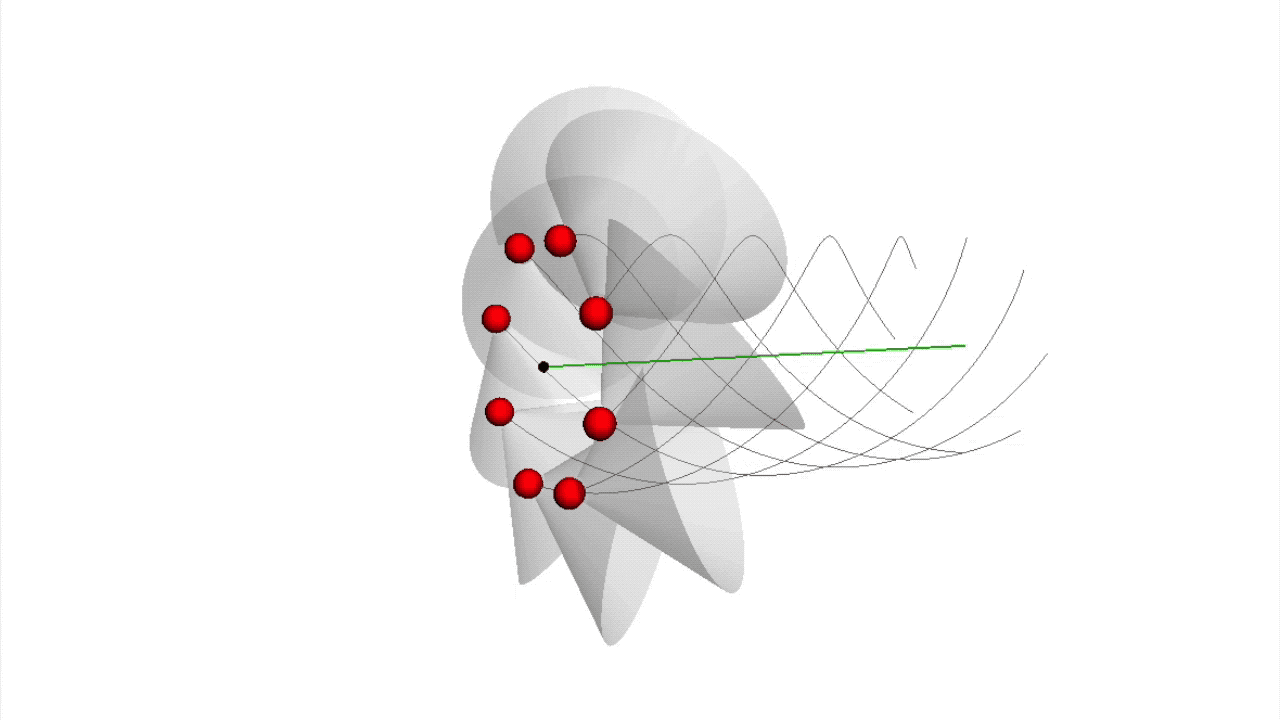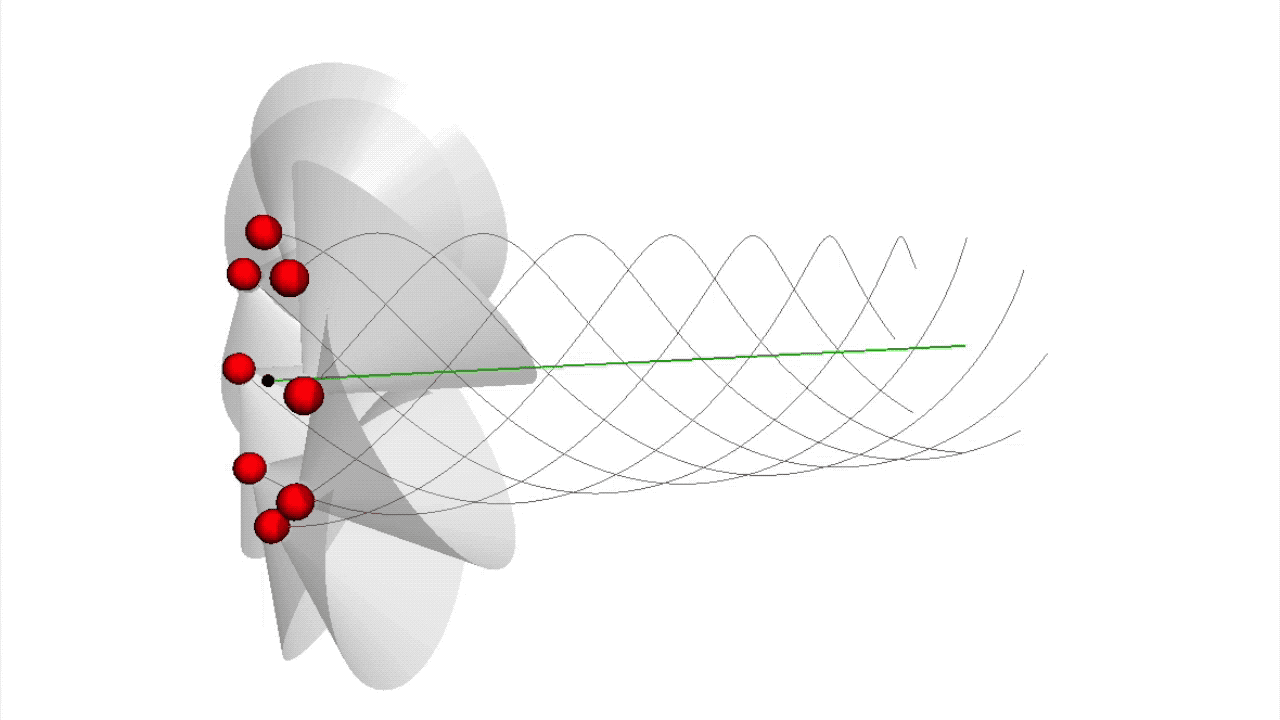
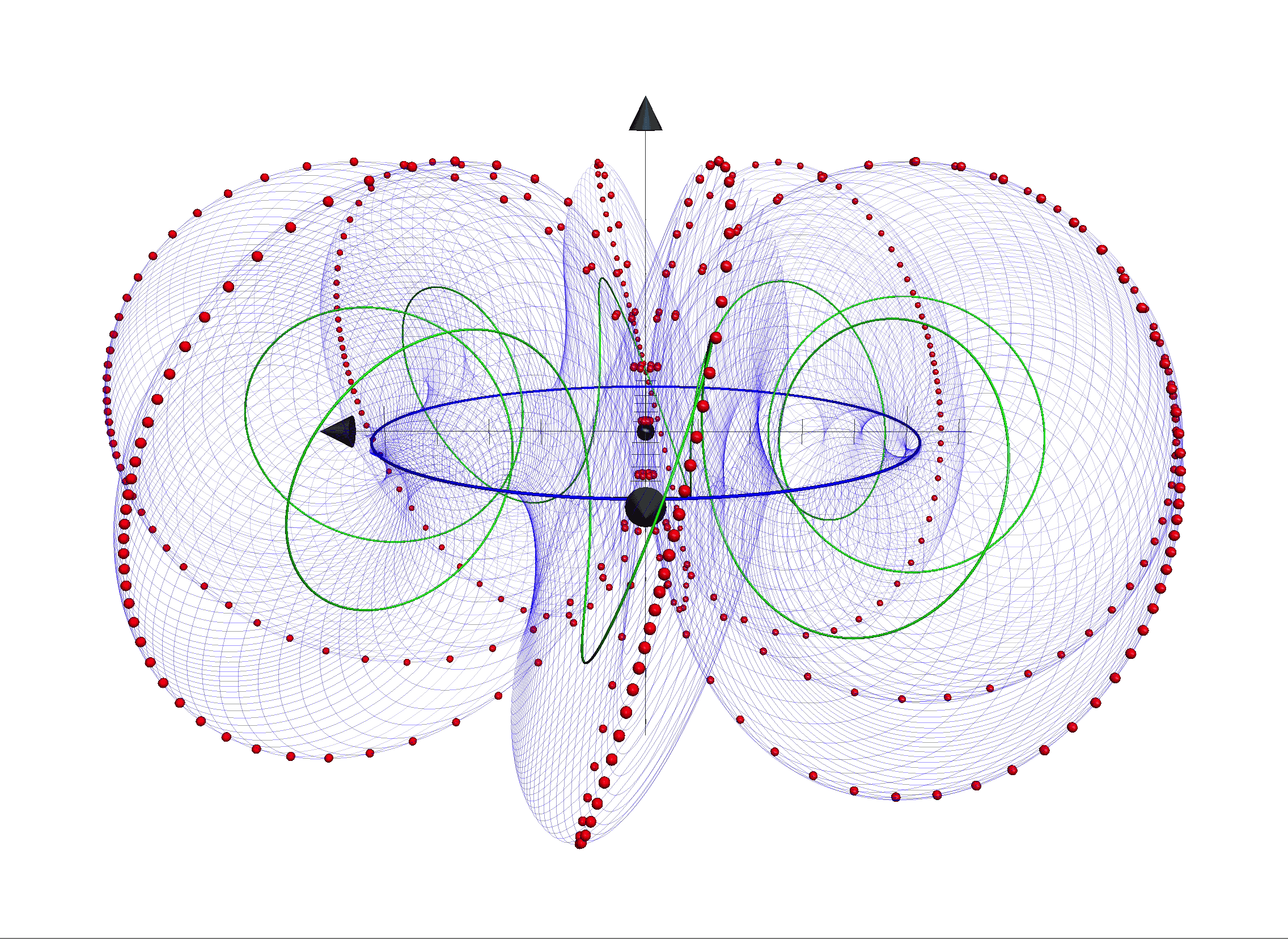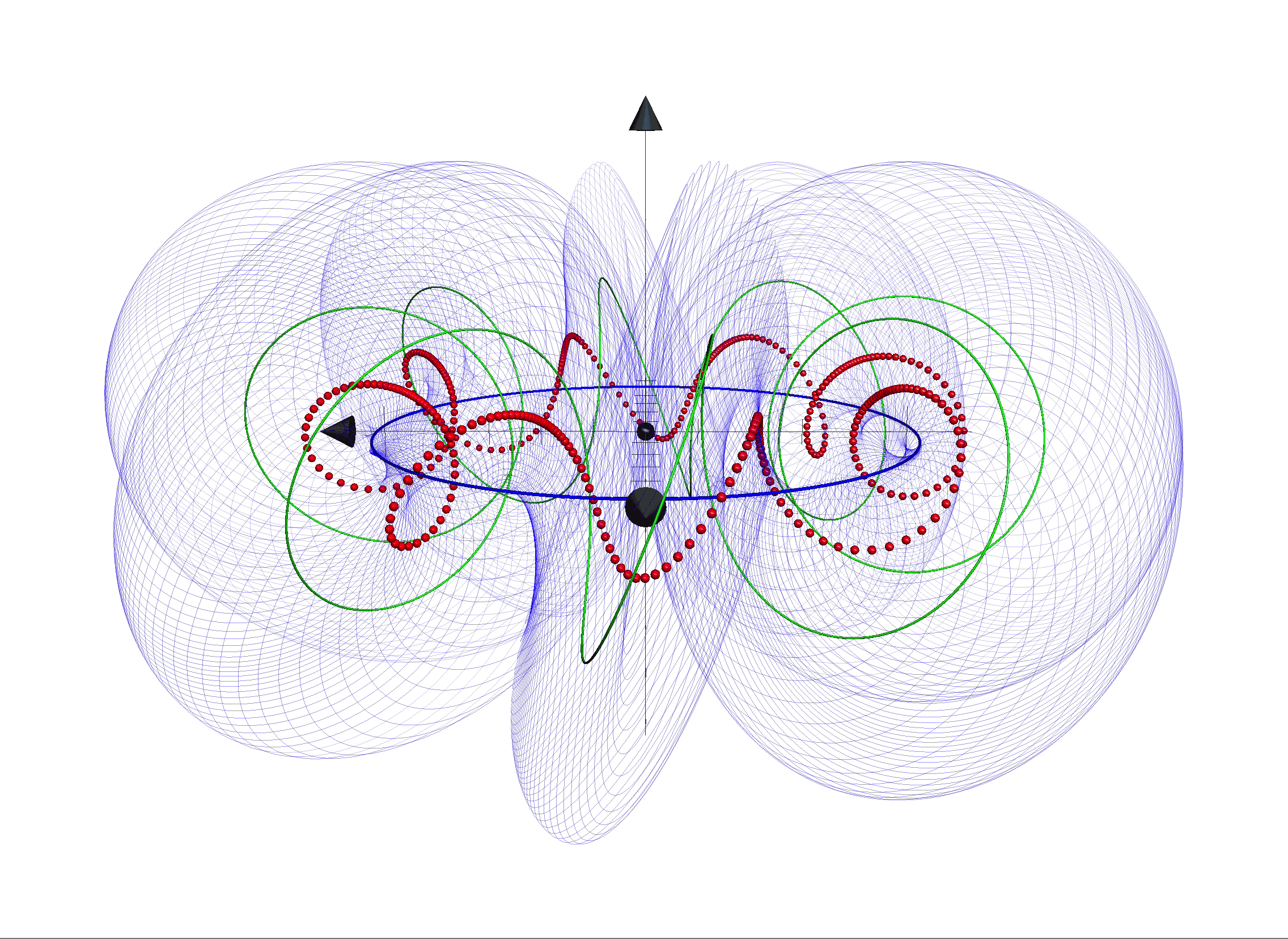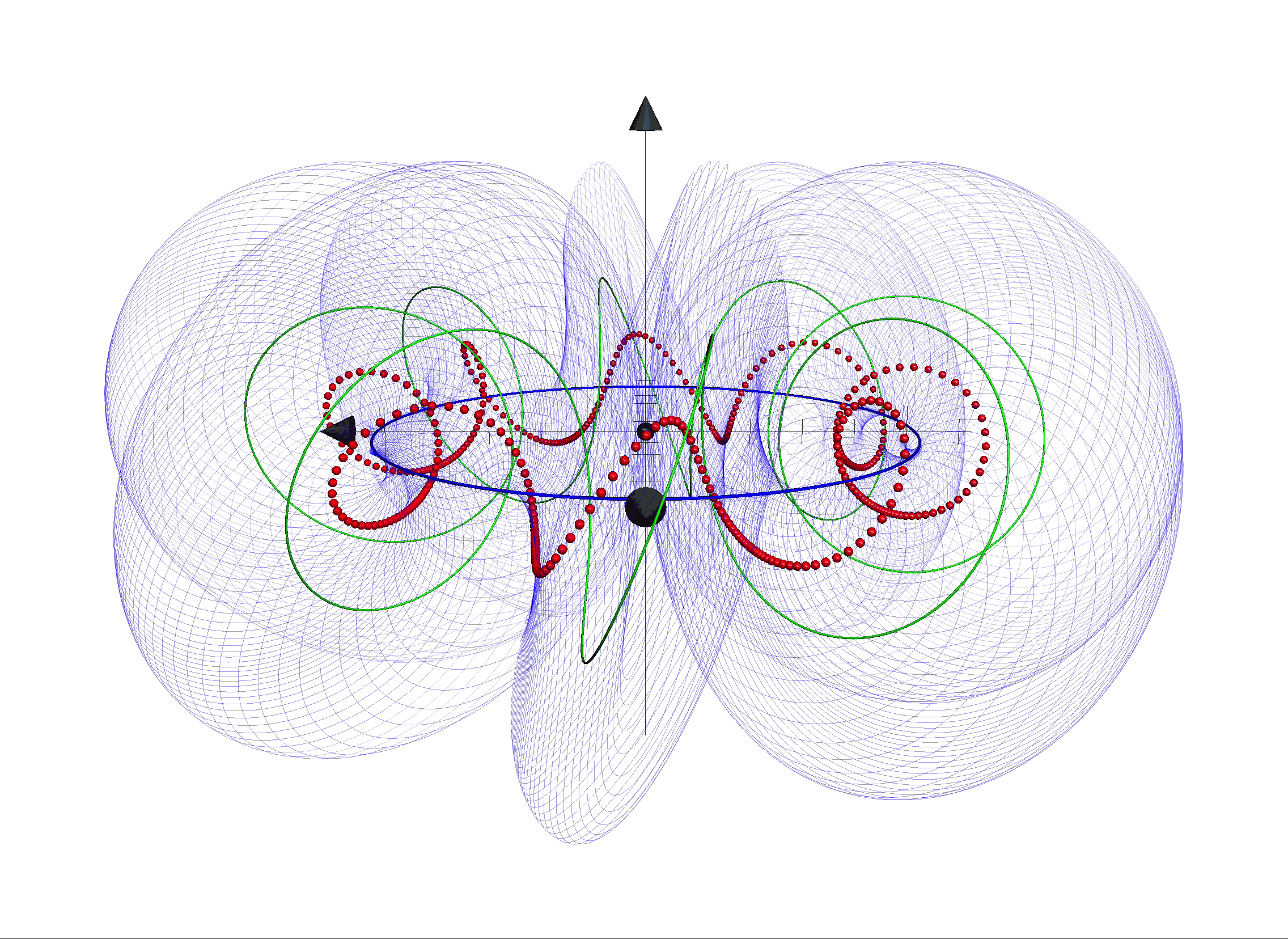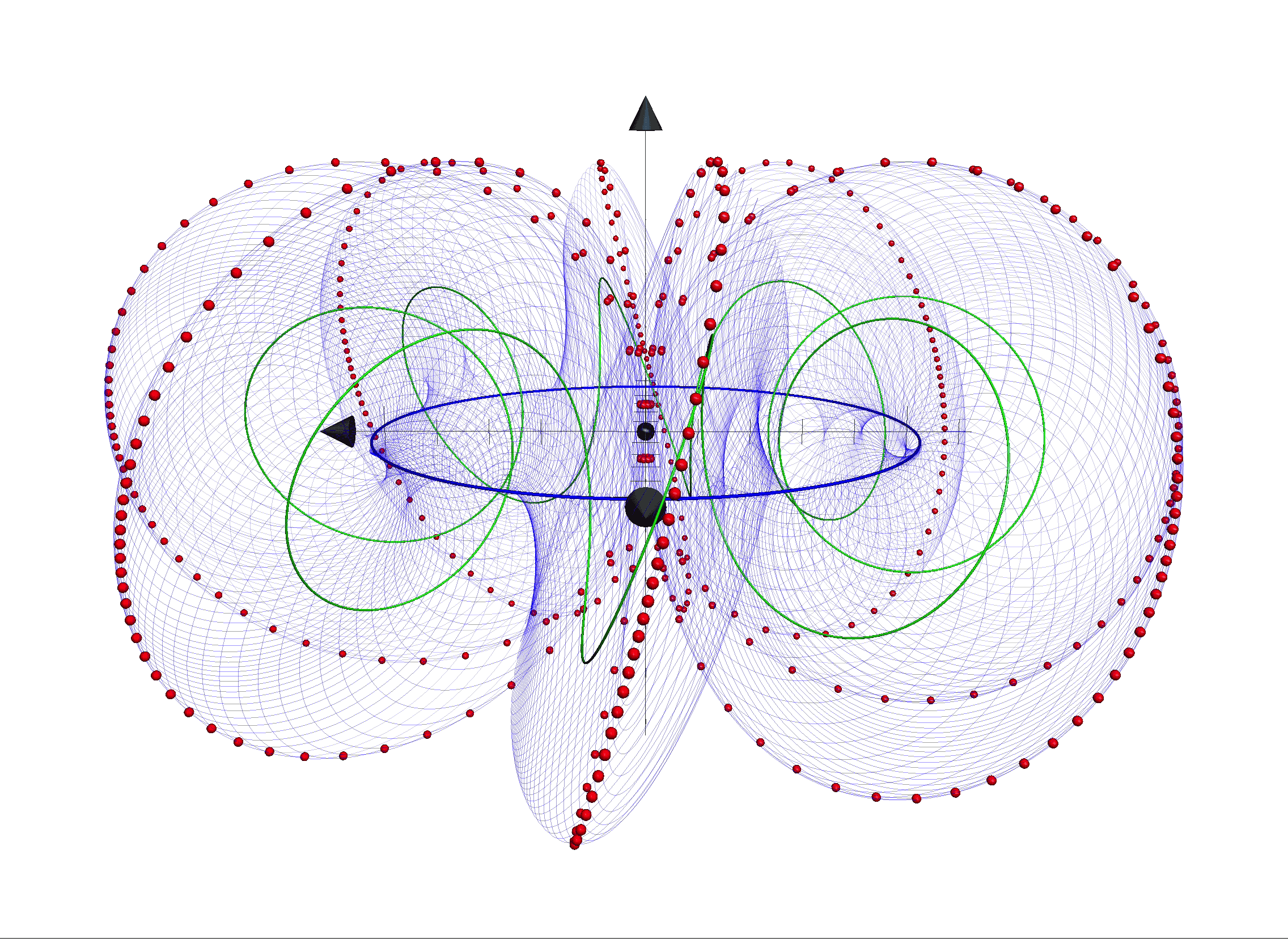
Eingebettet in einem Vakuum aus Wirkungsquanten sind die Wirkungsquanten-Strings der Elementarteilchen von einer Wolke aus virtuellen Teilchen umgeben. Die geometrische Struktur ihres Strings verleiht ihnen ihre Eigenschaften.
| ▾ | Notizen |
Interessante Aspekte
• Die Materiewelle und die Einstein-De-Broglie-Beziehungen, siehe Wikipedia Materiewelle.
Strukturelle Analyse
• Windungsanzahl der Doppelspirale des Leptonen-Modells:
Die bisher unbekannte Windungsanzahl oder „Sternspitzenanzahl“ könnte ggf. aus folgender Frage beantwortet werden.
Wieviele Kegeloberflächen der Wirkungsquanten-Impulskegel streifen einen Beobachter, wenn sich die Struktur bei ihrer Schwingung einmal öffnet und wieder schließt?
Dies wird vermutlich oder könnte zumindest ein ganzzahliger Anteil der gesamten Wirkungsquanten des Strings sein, der eventuell von der Windungsanzahl abhängt.
Sollte der Anteil von der Windungsanzahl abhängen, dann sollte die Windungsanzahl so groß sein, dass bei einer Schwingung die gesamte Anzahl der Impulskegel
des Strings den Beobachter streifen (siehe Quantengravitation der Elementarteilchen).
Wenn es diese Abhängigkeit nicht gibt, dann kann die Frage so wohl nicht beantwortet werden.
• Die Elapsonen haben ihre WW nur innerhalb ihres Strings, denn ein WQ kann nur das oder die benachbarten WQs beeinflussen.
Bei den Leptonen und Hadronen ist dies anders: Weil diese sich nicht mit LG bewegen kann die Farbpolarisation und die elektroschwache Polarisation
auf alle anderen Teile des Strings wirken.
• Der Leptonen-String eines geladenen Teilchens erscheint punktförmig, weil sein elektromagnetisches Feld – oder sogar genauer sein elektroschwaches Feld – so erscheint, dass seine Quelle im Schwerpunkt des Strings liegt.
Scheinbare Tabubrüche und vermeintliche Widersprüche zur heutigen Physik
• Nach dem Standardmodell der Teilchenphysik soll die Geschwindigkeit von Elektronen an ihrer Oberfläche nach ihrem magnetischen Drehmoment größer als die LG sein. (Vgl. YouTube. Lesch & Gaßner - Spins, Nichts und das Higgsfeld oder Stringtheorien und Schleifenquantengravitation | Harald Lesch & Josef M. Gaßner)
In der Quanten-Fluss-Theorie bestehen alle Elementarteilchen und auch das Vakuum aus den neu eingeführten Wirkungsquanten. Die Wirkungsquanten formieren sich in „Schwärmen“ zu schwingenden Strings, welche die Elementarteilchen darstellen. Dies gilt für Lichtteilchen – – ebenso wie für alle (mit Materieinhalt) – zum Beispiel Leptonen und Quarks.
Bei Teilchenkollisionen oder -reaktionen formieren sich Wirkungsquanten dieser Wirkungsquanten-Strings nach den Regeln der Erhaltungssätze um; die Schwärme gruppieren sich neu. Dies kann einfach eine Bewegungsänderung(Link) bedeuten oder auch eine Teilchenumwandlung. Da alle Eigenschaften der Elementarteilchen der Struktur ihrer Wirkungsquanten-Strings entspringt bedeutet jede Umformierung der Wirkungsquanten deren Veränderung.
Die Änderung der Anzahl der Wirkungsquanten in einem String bedeutet dabei zum Beispiel die Veränderung seiner Energie, da jedes Wirkungsquant einer Energieeinheit entspricht. Eine Änderung der Dichte der Wirkungsquanten in einem String-Abschnitt verändert seine elektrisches Feld(Link) oder seine . Exemplarisch ist hier zur Verdeutlichung die Animation eines Leptons dargestellt (siehe Film 1).
Die Wirkung eines einzelnen Wirkungsquants auf sein Umfeld entspricht dabei dem Planckschen Wirkungsquantum h.
Interessanter Weise ergibt sich die
dann aus einem
als statistisches Phänomen, wenn die Wirkungsquanten eines Elementarteilchens bei einem Messvorgang in einer bestimmten Zeit oder in einem bestimmten
Ortsintervall gezählt werden.
Wirkungsquanten verhalten sich wie kleine Wellen. Ein Wirkungsquanten-String erscheint wie eine Anhäufung von Wellen in einem „Wellenmeer“, da auch das Vakuum aus Wirkungsquanten besteht. Das Wellenmeer entspricht folglich dem und die Anhäufung von Wirkungsquanten in und um einen String herum dem , welcher die hervorbringt.
Die Wirkungsquanten eines Elementarteilchen-Strings üben einen beugenden oder ablenkenden Einfluss auf ihre Umgebung aus und reduzieren aufgrund ihrer Anhäufung die Lichtgeschwindigkeit in ihrem Umfeld. Es ergibt sich die Formel der Allgemeinen Relativitätstheorie für die Lichtgeschwindigkeit im Gravitationsfeld einer homogenen Massenkugel, bezogen auf den 3-dimensionalen Raum. Dieser Lichtgeschwindigkeitsgradient, der ein Elementarteilchen umgibt, übt eine anziehende Wirkung auf Elementarteilchen-Strings in seiner Umgebung aus, die sehr klein ist und der der Allgemeinen Relativitätstheorie entspricht.
|
|
In der und der ist nachfolgend dargestellt, wie die Struktur der verschiedenen Elementarteilchen im Prinzip aussehen. Die Darstellung eines fehlt noch und muss erstellt werden. Dazu existieren aber schon recht weitgehende Vorstellungen.
| → |
|
Elementarteilchen mit Ruhemasse |
|
Photonen (Lichtteilchen) |
|
In Arbeit …
| ← |
|
| ▾ | Notizen |
Können Photonen keine Ruhemasse haben?
• Photonen können eine Ruhemasse haben, wenn diese sehr klein ist:
– Siehe Video: Arvin Ash: Why No One Knows If Photons Really Are Massless: What if they Aren't?
XXX XXX XXX XXX XXX XXX XXX XXX XXX
XXX XXX XXX XXX XXX XXX XXX XXX XXX
In Arbeit …
| → |
|
| |
Massenträgheit |
|
In Arbeit …
| ← |
|
| ▾ | Notizen |
(• Massenträgheit entsteht in der FrQFT dadurch, dass sich die Struktur eines Teilchens durch einen Fluss von Wirkungsquanten ändern muss. Dieser Fluss, das Umbauen der Elementarteilchen, kostet Zeit. Diese Verzögerung ist Proportional zur Masse des Elementarteilchens. Denn je schwerer es ist, desto mehr Energie muss aufgewendet werden, dessen Bewegungszustand zu verändern, weil ein bestimmtes Verhältnis der Wirkungsquanten ausgetauscht werden muss. Dies führt auch zu den Erhaltungssätzen von Masse, Energie und Impuls.)
(• Ähnlich scheint es auch in der Heim-Theorie zu sein. Siehe Ordner: "Massenträgheit entspringt Strukturflüssen, wie in der FrQFT, die ART weiß dazu nichts zu sagen, außer das Machsche Prinzip - Burkhard Heim - Das neue Weltbild des Physikers - cd2v4-06")
XXX XXX XXX XXX XXX XXX XXX XXX XXX
XXX XXX XXX XXX XXX XXX XXX XXX XXX
In Arbeit …
| → |
|
| |
Elektrische Ladung |
|
Higgs-Feld, Higgs-Mechanismus und träge Masse |
|
In Arbeit …
• Lesen: Bezug zwischen der trägen Masse und dem Higgs-Feld. Siehe Raum, Zeit, Fortschritt: Kategorien des Handelns und der Globalisierung, S. 71-72. Den Verweisen nachgehen. Dieses Buch ins Literaturverzeichnis aufnehmen? Gibt viele Verweise und Anregungen. Das hier erwähnte Sirup-Bild passt eher nicht, weil dort Reibung eine Rolle spielt, die jeden Gegenstand zur Ruhe abbremsen würde.
In der FrQFT kommt die Trägheit daher, dass die Wirkungsquanten bei der Beschleunigung im Körper durch welche mit den neuen Bewegungseigenschaften ausgetauscht werden müssen, was Zeit kostet. Bezüglich der Gravitation gilt dies wohl nicht, weil durch sie die Wirkungsquanten gebeugt werden, was ihre Bewegungrichtung direkt ändern. Aber auch dies kostet Zeit.
In der Quanten-Fluss-Theorie XXX XXX XXX XXX XXX XXX XXX XXX
XXX XXX XXX XXX XXX XXX XXX XXX XXX
Weil sowohl die träge Masse als auch die schwere Masse der Gravitation aus der Anhäufung von Wirkungsquanten in und um die Elementarteilchen entstehen, wird verständlich, dass beide Massen einander gleich sein müssen. Die träge Masse entsteht aus der Zeit, die benötigt wird Veränderungen der Bewegung von den „angestoßenen“ Wirkungsquanten auf den Rest der zum Elementarteilchen gehörenden Wirkungsquanten zu übertragen. Die schwere Masse … XXX XXX XXX XXX …
In Arbeit …
| → |
Higgs-Feld und Higgs-Mechanismus — Vakuum, Higgs-Feld und Wechselwirkungen |
| |
Gravitation |
|
In Arbeit …
Das Dunkle-Materie-Phänomen … XXX XXX XXX XXX XXX XXX XXX XXX XXX
XXX XXX XXX XXX XXX XXX XXX XXX XXX
In Arbeit …
| |
Hadronen aus Quarks und Gluonen |
|
Quantenmechanik |
|
In Arbeit …
In der Welt der Quanten-Fluss-Theorie ergeben sich die Grundregeln der Quantenmechanik aus der Körnigkeit des neu eingeführten Bewegungsraums(Link)
in Form von Wirkungsquanten.
Diese Eigenschaft der diskreten Abzählbarkeit des neuen Modells wird auch in Experimenten – also in der Natur – beobachtet
und mündet in die berühmte Heisenbergsche Unschärferelation.
XXX
XXX
XXX
XXX
XXX
XXX
XXX
XXX
XXX
Heisenbergsche Unschärferelation
prinzipiellen Abzählproblem
XXX
XXX
XXX
XXX
XXX
XXX
XXX XXX XXX XXX XXX XXX XXX XXX XXX
In Arbeit …
| → |
| |
Welleneigenschaften der Elementarteilchen |
|
… ein neues Verständnis der Interferenz von Elementarteilchen am Beispiel des Doppelspaltexperiments
| ▾ | Notizen |
De-Broglie-Bohm-Theorie (Bohmsche Mechanik, Pilotwellentheorie von de Broglie und Bohm)
• Nach meinem neusten Verständnis (11/2018) korrespondieren die Welleneigenschaften der FrQFT mit der De-Broglie-Bohm-Theorie. Die Pilotwelle ist das Interferenzmuster des Vakuums. Die Elapsonen-Fluss-Projektion ist also die Pilotwelle. Dabei ist das Elementarteilchen, dass scheinbar hinter dem Doppelspalt interferiert, ein Teil des Interferenzmusters des Vakuums und wird aus diesem Grund auch von dieser Pilotwelle mitgetragen, denn das Elementarteilchen ist demnach wirklich ein Teil von ihr.
• Die De-Broglie-Bohm-Theorie bekommt in der FrQFT also eine klare Realisierung, die ihre fraglichen hypothetischen Annahmen physikalisch erklärt.
• In Kurzform ist die De-Broglie-Bohm-Theorie in folgendem Video erklärt: Kollaps der Wellenfunktion: Bohmsche Mechanik, Pilot Wave, Multiversen | AzS (34) | Josef M. Gaßner. URL: https://www.youtube.com/watch?v=THu3tWcZnC4
– Wie Herr Gaßner ab Sekunde 09:04 und dann 10:40 erklärt, ist die De-Broglie-Bohm-Theorie nicht wiederlegt worden, sondern aktuell immer noch eine der Interpretationsmöglichkeiten der Quantenmechanik.
– Herr Gaßner stellt fest, dass Heisenbergs Unschärferelation erhalten bleibt, aber der Ort ihrer Wirkung auf die Ausgangssituation verlegt wird und nicht auf die Messung. Da bin ich mir nicht ganz sicher, ob dies so ganz stimmt. Mit der FrQFT bekommt die Heisenbergsche Unschärferelation jedenfalls auch eine physikalische Realisierung und ergänzt damit auch in dieser Hinsicht die De-Broglie-Bohm-Theorie.
– Herr Gaßner stellt fest, dass die Schrödinger-Gleichung so nicht stimmen kann und dass in der Quantenmechanik nichts entstehen und vergehen kann. Siehe Sek. 16:37.
– In der FrQFT kann etwas entstehen und vergehen! Auch insofern ergänzt sie die De-Broglie-Bohm-Theorie und sogar die ganze Quantenmechanik.
Aktuelle Fachdiskussion
• Unerklärliches Phänomen in der Quantenphysik? Siehe: Quantenzigarren in rätselhaftem Gleichtakt. In: Spektrum der Wissenschaft 09/2018. 26-28.
• Wann und wie gehen die Bereiche der Quantenphysik und der klassischen Physik ineinander über? Siehe: An der Grenze zur Quantenwelt. In: Spektrum der Wissenschaft 08/2018. 12-17.
• Inwieweit entspricht das hier vorgestellte Interferenzmuster des Vakuums der Pilotwellentheorie von de Broglie und Bohm? Siehe Val Baker, Amira, It’s a Particle Interacting with the Associated Wave Field! URL: https://resonance.is/particle-interacting-associated-wave-field/
• Wellen- und Teilcheneigenschaften sollen zusammen gebracht worden sein, siehe Coles, »Equivalence of wave–particle duality to entropic uncertainty« und Sekundärliteratur: Lingenhöhl, »Ist die Quantenphysik weniger kompliziert?«
In einem Artikel auf http://www.quantumlah.org/highlight/141220_wave_particle.php ist zu lesen: »›The connection between uncertainty and wave-particle duality comes out very naturally when you consider them as questions about what information you can gain about a system. Our result highlights the power of thinking about physics from the perspective of information,‹ says Wehner, who is now an Associate Professor at QuTech at the Delft University of Technology in the Netherlands.«
Ich hatte schon festgestellt, dass Photonen, also Zirkular polarisierte Elapsonen, Wellen- und Teilcheneigenschaften haben. Welleneigenschaften durch ihre Rotation und Wechselwirkung mit den Vakuum-Elapsonen und Teilcheneigenschaften, weil sie ein zusammen hängendes Gebilde sind.
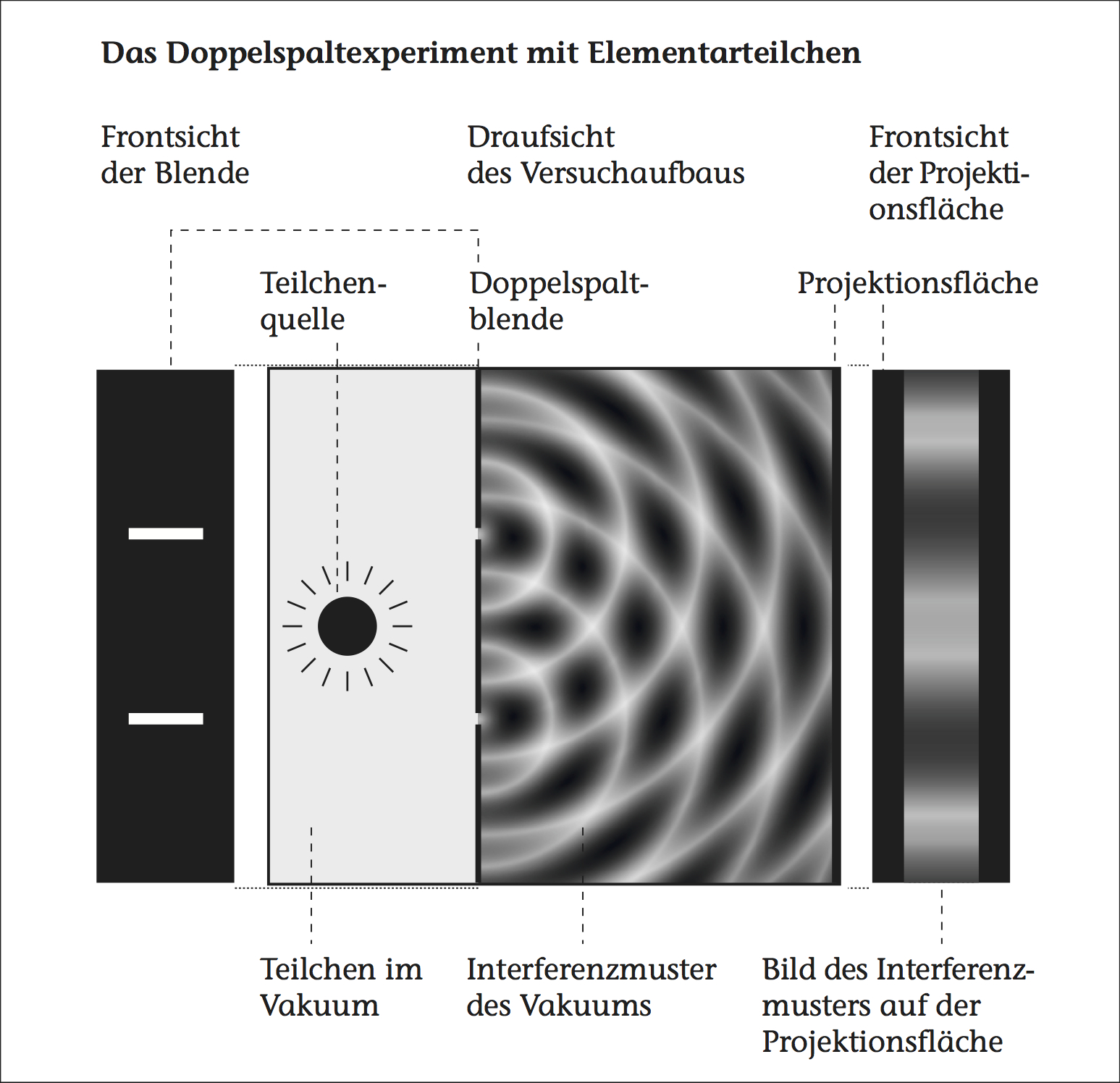
Beim Doppelspaltexperiment wird ein diffuser Strahl, bespielsweise aus Elektronen, auf eine Doppelspaltblende projeziert. Das sich ergebende Bild wird auf einem hinter der Blende positionierten Schirm detektiert (siehe ).
|
Bemerkenswert an diesem Experiment ist das Auftreten des Interferenzmusters selbst dann, wenn nur ein Elementarteilchen zur selben Zeit durch die Spalte fliegt und daher eigentlich keine Interferenz zwischen Elementarteilchen auftreten kann, weil keine Teilchen zur selben Zeit am selben Ort sind.
Die neue Interpretation des Experiments geht von einem Interferenzeffekt aus, der auf eine direkte Wechselwirkung zwischen den Elementarteilchen völlig verzichten kann. Es geht vielmehr um eine Wechselwirkung zwischen einem sowieso durch den Versuchsaufbau im Raum vorhandenen, statischen Interferenzmuster des Vakuums und jedem einzelnen Elementarteilchen, welches durch einen der Spalte Richtung Schirm geflogen ist.
Interferenzmuster des Vakuums
Um zu verstehen, wie sich im Vakuum, aufgrund des bloßen Vorhandenseins der Doppelspaltblende, ein Interferenzmuster
herausbilden kann, hilft es, sich zunächst mit einem verwandten Phänomen zu beschäfftigen, dem Casimir-Effekt.
Anders als bei der Interferenz, geht es beim Casimir-Effekt um Kräfte, welche das Vakuum auf zwei Platten ausüben
kann, die sich räumlich sehr nahe beieinander befinden. Die Erklärung der heutigen Physik besagt, dass der
Casimir-Effekt auf einer Einschränkung des Frequenzspektrums der sogenannten Quantenfluktuationen des
Vakuum zwischen den Platten beruht.
Außerhalb des Plattenspalts ist hingegen ein kontinuierliches Spektrum im Vakuum vorhanden.
Dieser Unterschied übt von außen eine Kraft auf die Platten aus, welche die Platten aufeinander zu drückt.
Das Vakuum der Quanten-Fluss-Theorie besitzt nun besondere Eigenschaften:
Es besteht aus wellenartigen Wirkungsquanten, die alle zusammen einen Bewegungsraum bilden.
Die Wirkungsquanten bewegen sich sehr konstant auf helixförmigen Spiralbahnen, deren
Translationsgeschwindigkeit der Lichtgeschwindigkeit im Dreidimensionalen Raum entspricht; daher der neue Begriff Bewegungsraum.
Ihre Rotationsfrequenzen besitzen im Vakuum ein nahezu kontinuierliches Spektrum.
Bei ihrer Bewegung durch den Raum sind die Wirkungsquanten idealisierter Weise – also im Durchschnitt – zu kreisrunden, ringförmigen Strings organisiert,
die aus diesem Gund elektrisch unpolarisiert erscheinen.
Diese ringförmigen Strings nenne ich Elapsonen.
Sie verhalten sich wie Lichtteilchen ohne elektromagnetisches Feld und
bewegen sich in Massen in alle Richtungen durcheinander und bilden so das Vakuum.
Befindet sich nun eine Doppelspaltblende im Vakuum, so können sich die Elapsonen im Vakuum nicht völlig ungehindert ausbreiten.
Ähnlich dem Casimir-Effekt können nur Elapsonen bestimmter Frequenzen und damit Wellenlängen zwischen den Spaltwänden existieren und so die Spalte passieren.
Die kontinuierliche Bewegung der Elapsonen des Vakuums und der Filtereffekt der Doppelspaltblende erzeugen zwischen der Blende und dem Schirm ein Interferenzmuster im Vakuum.
Denn die durch die Doppelspaltblende gefilterten Elapsonen haben untereinander durch den Prozess des Filterns sehr ähnliche Welleneigenschaften und bewegen sich von den Spalten ausgehend Richtung Schirm und interferieren deshalb miteinander, wie man es von solchen Wellen im Raum erwartet.
Wirkung des Interferenzmusters auf Elementarteilchen
Elementarteilchen, die gemeinsam mit den gefilterten Elapsonen die Doppelspaltblende in Richtung Schirm passieren werden ebenfalls gefiltert und haben daher auch entsprechende Welleneigenschaften wie diese. So interferieren diese Elementarteilchen mit dem Interferenzmuster der Elapsonen zu einem Gesamtinterferenzmuster (siehe ).
Ich folgere, dass das Doppelspaltexperiment ein Interferenzmuster des Vakuums sichtbar macht, welches durch die
Filterwirkung der Doppelspaltblende im Bewegungsraum der Quanten-Fluss-Theorie erklärt werden kann.
Die bisherige Interpretation „einzelne Elementarteilchen, welche durch einen der Spalte gehen, interferierten mit sich selber“(Verweis) wäre folglich nicht zutreffend.
Vielmehr interferieren diese Elementarteilchen mit dem durch diesen Effekt im Vakuum vorhandenen
Interferenzmuster, weil es die gleiche Frequenz wie sie selber trägt.
Wird das Experiment zusätzlich auf eine Messung ausgelegt, die den Spalt ermittelt, welchen die Elementarteilchen
passieren, dann werden die Elementarteilchen so von ihrem Weg abgebracht, dass das Experiment das Interferenzmuster des Vakuums
nicht mehr sichtbar machen kann.
(Begründen warum: Beeinflusst nur die Messung des Teilchenorts das Experiment, oder auch die Messaperatur das Interferenzmuster des Vakuums? Nachlesen!)
In diesem Sinn ist das Doppelspaltexperiment ein Nachweis der Vakuuminterferenzmuster, welche die Quanten-Fluss-Theorie vorhersagt und hier allgemeiner Elapsonen-Fluss-Projektionen genannt werden. Nach meinem Eindruck korrespondieren die Elapsonen-Fluss-Projektionen mit der De-Broglie-Bohm-Theorie und ich versuche auf einer separaten Seite beide Ansätze zueinander zu bringen.
(Eventuell ist ein modifizierter Erklärungsansatz notwendig, um den Pfadintegralen der Feynman'schen Formulierung der Quantenmechanik gerecht zu werden:
Danach sendet die Quelle der Elementarteilchen gleichzeitig zu diesen in Massen durch Elapsonen gebildete, virtuelle Elementarteilchen der gleichen Frequenz aus.
Diese virtuellen Elementarteilchen nehmen dann alle möglichen Wege deren Wahrscheinlichkeit größer als Null ist, weil sie sich im Wesentlichen wie Elementarteilchen verhalten.
Dabei interferieren die virtuellen mit den normalen Elementarteilchen, wodurch jedes virtuelle Elementarteilchen am Ende – also bei der Messung – zum normalen Elementarteilchen werden kann.
Besonders interessant wäre dann was genau „im Wesentlichen“ heißt.
Um zu beurteilen, ob diese Alternative notwendig ist, wäre es ein Ansatz zu gucken, wie eine Beobachtung zwischen Quelle und Blende das Bild auf dem Schirm verändert.
Würde die Beobachtung das Bild auf dem Schirm zerstören, so könnte die Alternative notwendig werden, wenn der Ort der Quelle eine Rolle zu spielen scheint.)
(Eine generelle Möglichkeit die Natur der Abstrahlungen der Quelle im Doppelspaltexperiment zu testen geht über die Impulserhaltung:
Die Frage ist, welchen Vektorimpuls erhält die Teilchenquelle durch die Abstrahlung der Elementarteilchen und zu welchem Zeitpunkt wird er auf die Quelle übertragen?
Dahinter steht, ob jedes einzelne abgestrahle Teilchen zum Zeitpunkt der Abstrahlung jeweils einen sich in der Richtung unterscheidenden Impuls auf die Quelle überträgt.
Wenn ja, wäre bekannt, durch welchen Spalt es geht.
Oder gibt die Wellenfront, die allen möglichen Wegen entspricht einen Gesamtimpuls ab, der dann in seiner Richtung immer gleich ist?
Oder wird der Impuls erst beim Detektieren durch Beobachtung auf dem Weg oder durch den Schirm auf die Quelle übertragen?
Wird ein Impuls auch dann auf die Blende übertragen?, wenn ein Teilchen durch einen der Spalte geht?
Wenn ja, könnte dann auch innerhalb einer der Blendespalte das Interferenzmuster erzeugt werden?
Was ergibt eine Messung des Vektorimpulses, welcher auf den Schirm übertragen wird?
Darüber könnte eventuell festgestellt werden, durch welchen Spalt das Teilchen kam.
Nebenfrage: Wird schon durch die Messung des Quellimpulses und/oder des Blendenimpulses und/oder des Schirmimpulses das Interferenzmuster auf dem Schirm zerstört?)
| → |
Quantenmechanik — Leptonen-Modell |
| → |
Welle-Teilchen-Dualismus — Leptonen-Modell |
| → |
| |
Virtuelle Teilchen |
|
In Arbeit …
Die Abstrahlungen des konstituierenden Wirkungsquanten-Strings erzeugt im umgebenden Vakuum virtuelle oder besteht selbst aus virtuellen Teilchen. Bezüglich der Gravitation sind dies virtuelle Wirkungsquanten, welche abgestrahlt werden. Diese verursachen eine Anhäufung von Wirkungsquanten des Vakuums um das konstituierende Elementarteilchen, welche seine Masse und Energie erhöhen – Higgs-Mechanismus. Bezüglich der elektroschwachen Wechselwirkung ist dies ähnlich. Der String-Versatz der starken Wechselwirkung aus dem Wirkungsquanten-Rotationszentrum heraus sollte auch ähnliches hervorbringen. XXX XXX XXX XXX
XXX XXX XXX XXX XXX XXX XXX XXX XXX
In Arbeit …
| |
Verschränkung |
|
Die Entwicklung eines Bildes
Eine Beschreibung der Verschränkung in Bezug auf den Spin von Elektronen wird hier beschrieben: Sachdev, »Stringtheorie für Festkörper«, S. 43-45. XXX XXX XXX XXX XXX XXX XXX XXX
» Verschränkung bedeutet Überlagerung von zwei Zuständen. Angenommen, zwei Elektronen, von denen eines UpSpin und das andere DownSpin aufweist, sitzen an unterschiedlichen Orten im Festkörper. Da Elektronen prinzipiell ununterscheidbar sind, lässt sich nicht sagen, welches up und welches down ist; bei de sind mit gleicher Wahrscheinlichkeit up oder down. Wir wissen nur: Wenn wir an dem einen Elektron Aufwärtsspin messen, weist der andere Spin garantiert abwärts. Anders gesagt, beide Spins sind antikorreliert. Kennen wir einen, so wissen wir auch über den anderen Bescheid. Auf den ersten Blick mutet die Verschränkung gar nicht seltsam an. Antikorrelationen gibt es oft: Wenn man den ei nen Schuh vor die Haustür stellt und den anderen in den Hin terhof, dann weiß man, sobald man an dem einen Ort den linken Schuh findet, sofort, dass der andere der rechte sein muss. Das Quantenphänomen ist aber vertrackter. Ein Schuh ist immer entweder der linke oder der rechte, selbst wenn man nicht weiß, welcher von beiden er ist; doch der Spin eines Elek trons wird erst durch den Messvorgang definiert. Das Elektron hat gewissermaßen zugleich Spin up und Spin down, bis es durch eine Messung gezwungen wird, sich zu entscheiden. Rätselhaft ist, wie die Elektronen antikorreliert bleiben. Wenn ein Elektron durch Messung einen definierten Spin bekommt, steht der andere Spin sofort auch fest. Woher wis sen sie, dass sie gegensätzliche Spins einnehmen müssen? Anscheinend gelangt die Information über den Quanten zustand des ersten Teilchens augenblicklich zum zweiten. Tatsächlich hat keines der beiden einen eigenen Quanten zustand, sondern nur das Teilchenpaar als Ganzes. Diese Nichtlokalität fand Einstein als »spukhafte Fernwirkung« so fragwürdig, dass er gleich die gesamte Quantenmechanik für ergänzungsbedürftig hielt. Unterdessen hat sich die Nichtlokalität in zahlreichen Ex perimenten bestätigt XXX XXX XXX XXX XXX XXX XXX XXX «
Fragen:
• Welche Observablen (siehe Wiki http://de.wikipedia.org/wiki/Quantenverschränkung) können Verschränkt sein? Nur der Spin oder auch andere?
XXX XXX XXX XXX XXX XXX XXX XXX XXX
In Arbeit …
| |
Punktförmige Erscheinung |
|
In Arbeit …
Warum kann ein Wirkungsquanten-String mit Ausdehnung ein fast Punktförmig erscheinendes Teilchen darstellen? Die Erste Frage ist, was erscheint Punktförmig an einem Elementarteilchen? Die Struktur der schwachen WW weißt auf eine Ausdehnung hin. Das magnetische Moment eines Elektrons weißt daraufhin, dass es sich wie ein Magnet mit Nord- und Südpol verhält (vgl. SdW 12/2013 Preonen-Artikel. S. 52.) Ich vermute das elektromagnetische Feld erschein erscheint Punktförmig. Schwingt es, wie in der FrQFT? XXX XXX XXX XXX XXX XXX XXX XXX
XXX XXX XXX XXX XXX XXX XXX XXX XXX
In Arbeit …
| |
Fußnoten |
|
| 1. |
(Primärliteratur einfügen!) Internet: Vgl. Max Planck Institute for Gravitational Physics, »Ruhemasse«. Vgl. Wikipedia, Masse, Spezielle Relativitätstheorie, Ruhemasse. | |
| 2. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Higgs-Mechanismus. | |
| 3. |
(Primärliteratur einfügen!) Internet: Vgl. Max Planck Institute for Gravitational Physics, »Ruhemasse«. Vgl. Wikipedia, Masse, Spezielle Relativitätstheorie, Ruhemasse. | |
| 4. | XXX | |
| 5. |
Vgl. Feynman, Feynman-Vorlesungen, Quantenmechanik, Kap. 1 Quantenverhalten, 1.4 Ein Experiment mit Elektronen, S. 5-7, hier S. 6. Vgl. Wikipedia, Doppelspaltexperiment, Experimentelle Beobachtung. | |
| 6. | Vgl. Huß, Die Gravitonen-Fluss-Theorie, v7.381, Kap. 5.4 Welleneigenschaften, S. 109-110. | |
| 7. | Vgl. Wikipedia, Casimir-Effekt. | |
| 8. | Vgl. Wikipedia, Casimir-Effekt, Vereinfachte Darstellung. | |
| 9. | Vgl. Huß, Die Gravitonen-Fluss-Theorie, v7.381, Kap. 3.2 Ansatz der Realisierung der Grundannahmen, S. 41-48, hier S. 42-44, u. a. Abbildung 3.2. Wirkungsquanten werden hier noch als Gravitonen bezeichnet. | |
| 10. | Vgl. Huß, Die Gravitonen-Fluss-Theorie, v7.381, Kap. 5.4 Welleneigenschaften, S. 109-110, hier S. 109. Wirkungsquanten werden hier noch als Gravitonen bezeichnet. | |
| 11. | Vgl. Feynman, Feynman-Vorlesungen, Quantenmechanik, Kap. 1 Quantenverhalten, 1.6 Beobachtung der Elektronen, S. 8-12. | |
| 12. | Vgl. Huß, Die Gravitonen-Fluss-Theorie, v7.381, Kap. 5.4 Welleneigenschaften, S. 109-110, hier S. 109. Wirkungsquanten werden hier noch als Gravitonen bezeichnet. |
| |
Stand 20. November 2025, 23:00 CET.
-
Permanente Links:
(Klicke auf die Archivlogos
zum Abruf und Ansehen
der Archive dieser Seite.) -

-
archive.todaywebpage capture