| ← |
Die arithmetische Struktur der Geometrie
Ein aktual unendliches Fraktal aus Primzahlteilen führt uns zur superialen Basis $ \s $
| ▾ | Notizen |
Ist die Geometrie fraktal? – Sind ein Punkt, eine Linie, eine Fläche und der Raum fraktal?
• Das Problem der Geometrie, eine Linie aus Punkten aufzubauen (Verwandt mit der Kontinuumshypothese): Die nullte, die erste und die zweite Dimension haben keine Ausdehnung, kein Volumen, – also Punkt, Linie und Fläche – und in gewisser Weise existieren sie so nicht. Aber mit ihnen sollen wir die dritte Dimension aus Punkten (Ecken) und Flächen konstruieren, die dann eine Ausdehnung hat und plötzlich existiert. Das scheint komisch und merkwürdig. Siehe Nassim Haramein, Die Entschlüsselung des Universums, S. 11-14, hier S. 12-13.
– Es geht einfach darum, wie man aus Punkten eine Linie exakt konstruieren kann: Handelt es sich wirklich um einen absolut unendlich kleinen Punkt, dann bekommen wir ein Problem. Es scheint mir, dass ein strukturierter Punkt, mit aktual unendlich kleiner Ausdehnung hier Abhilfe schaffen kann. Ich kann nämlich in Form von aktual unendlich großen Zahlen beschreiben, wie oft ich diesen superialen Punkt aneinander legen muss. Dies kann ich bei absolut unendlich kleinen Punkten nicht tun.
– Bietet hier die aktual unendlich kleine Hülle der superial-kleinen Zahlen um einen Punkt einen logischen Lösungsansatz für die Geometrie? Denn bei einem absolut unendlich kleinen Punkt können wir nicht sicher und exakt definieren, wie oft wir ihn aneinander legen müssen, um eine Gerade einer bestimmten Länge zu erzeugen. Bei einem Punkt mit superial-kleiner Hülle ist dies wohldefiniert.
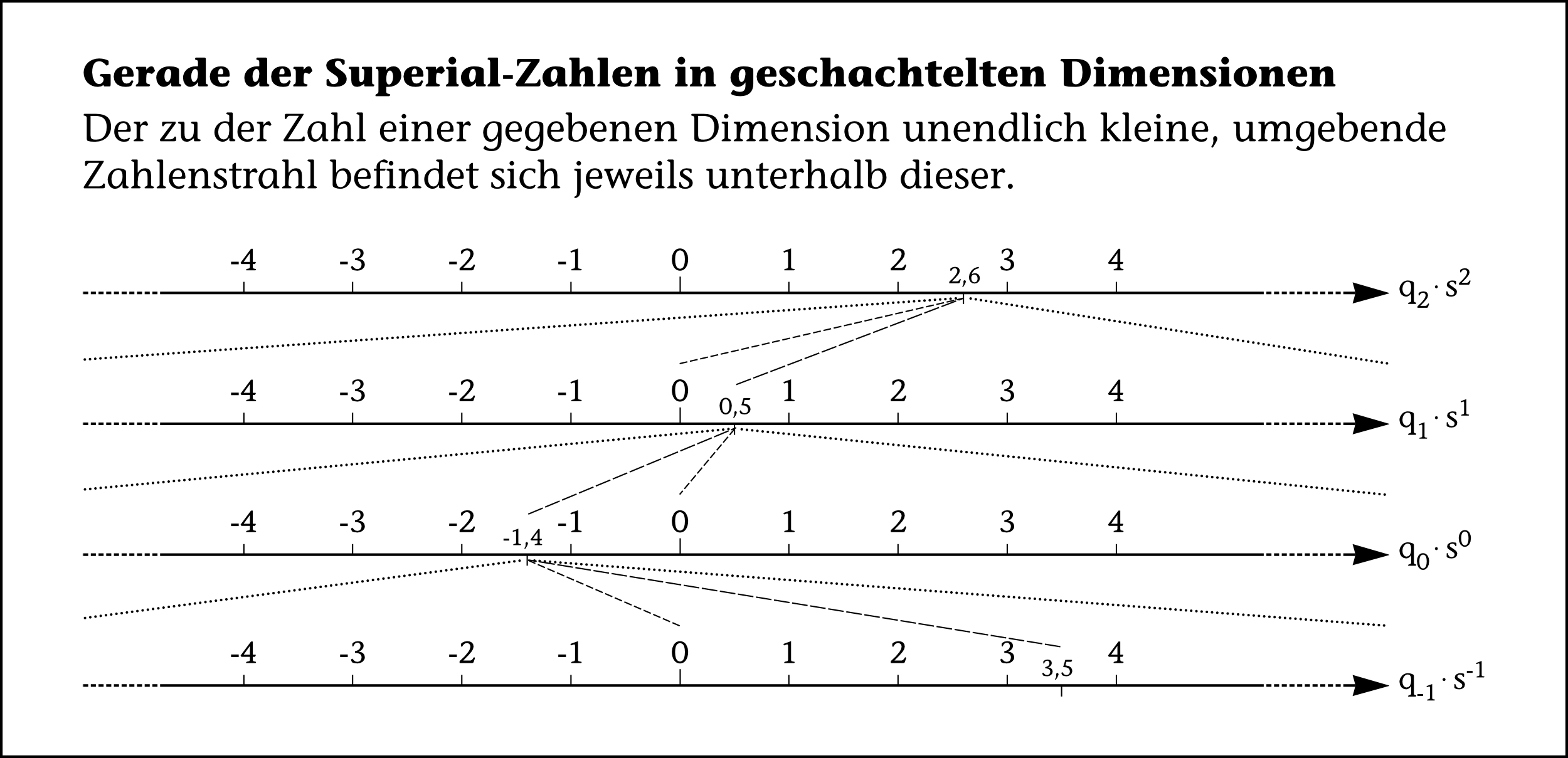
⋅ In Bezug auf die Ordinalzahlen und Biordinalzahlen ist die „Umgebung“ übrigens das „Fähnchen“ zwischen der Null und Ein bzw. zwischen jeder ganzen Zahl, mit dieser, und der nächst größeren, ohne diese, obwohl die Zahlen dazwischen in den ganzen Zahlen gar nicht definiert sind. Sie sind aber implizit mit gemeint. Siehe Abbildung 1.
– Ist die Geometrie also eigentlich fraktal? Was durch die Analysis, mit ihren Ableitungen und Integralen, schließlich sichtbar wird?
Welche Form der Vollständigkeit haben die reel algebraischen Zahlen?
• Ich würde es algebraische oder geometrische Vollständigkeit nennen.
• Welche Form der Vollständigkeit haben dagegen die reellen Zahlen?
– Weitz / HAW Hamburg: Der Aufbau des Zahlensystems – Sek. 11:10
– Hierfür müssen wir vermutlich eine superiale Vollständigkeit definieren. Mit den Superial-Zahlen erster Stufe, wie wir sie hier vornehmlich definieren, erreichen wir die superiale Vollständigkeit allerdings noch nicht, wie wir an der superialen Eulerschen Zahl sehen. Edmund Weitz sagt allerdings, dass wir diese Vollständigkeit in $ \mathbb{R} $ zeigen können.
In der Geometrie stoßen wir auf ein fundamentales Problem. Denn wollen wir beispielsweise eine Linie konstruieren oder berechnen, so wird allzu oft leicht dahin gesagt:
Nun setzen wir die Linie aus vielen Punkten zusammen; natürlich aus unendlich vielen, um wirklich eine geschlossene Linie zu erhalten.
Oder entsprechend für eine Fläche:
Nun setzen wir die Fläche aus vielen Linien zusammen; natürlich aus unendlich vielen, um wirklich eine geschlossene Fläche zu erhalten.
Und Entsprechendes so fortgeführt für den Raum beziehungsweise das Volumen und jede nächst größere Dimension. Doch was ist eine Linie, um beim einfachsten Beispiel zu bleiben, und wie können wir eine Linie aus Punkten aufbauen?
Ein fundamentales Problem
Keine Hochstapelei
Der Versuch eine Linie aus Punkten quasi aufzustapeln ist zum Beispiel zum Scheitern verurteilt. Beim Stapeln wird ein Punkt so an den anderen platziert, dass alle gemeinsam die Linie füllen, dicht an dicht. Diese Dichte ist allerdings davon abhängig, welche Ausdehnung jeder einzelne Punkt hat. Daher das Wort stapeln.
Ein Punkt besitzt aber per Definition keine Ausdehnung. Daher können wir Punkte nicht so stapeln, dass eine Linie gefüllt wird. Dies gelingt auch dann nicht, wenn wir unendlich viele Punkte nehmen. Denn diese Art von großer Unendlichkeit, die Punkte ohne jede Ausdehnung raumgreifend stapeln kann, scheint unmöglich.
Gleiches gilt auch für all die anderen genannten Objekte: Wir können Linien ohne jede Breite nicht zu Flächen stapeln und so fort. Auf diese Weise ist also kein Konstruieren einer höheren Dimension aus niedrigeren Dimensionen möglich.
Aber was funktioniert dann?
Ist die Geometrie im Grunde fraktal?
Weben oder Netzwerken
Wir können uns zwei Punkte denken, die nicht aneinander – also nicht aufeinander – liegen und darum einen Abstand haben. So geben diese Punkte auch eine Richtung vor und wir können sie sinnvollerweise mit Null und Eins bezeichnen.
Nun beginnen wir ein Netz von Punkten zu „weben“, indem wir zwischen beide Punkte, genau in der Mitte, einen weiteren Punkt legen und haben nun drei Punkte in der selben Richtung auf einer Linie. So fahren wir fort und legen jeweils zwischen zwei benachbarte Punkte einen weiteren in die Mitte. Hierdurch wird das Gewebe zwischen unseren Ausgangspunkten immer dichter gewebt und wir spannen ein Netz von Punkten auf, wodurch wir immer mehr Punkte auf der Strecke zwischen Null und Eins erhalten.
Selbstähnlichkeit
Die Auflösung und Struktur des Inneren
Weil wir immer wieder das gleiche tun, ergibt sich eine fraktale, also selbstähnliche, Netzstruktur.
Die gesamte Anzahl der Punkte $ n $ sowie ihre Koordinaten $ r $, ihre Dichte, als auch die Anzahl der Teilstrecken, $ \rho $ und ihr Abstand $ d $ berechnen sich mit der Fraktalebene $ x $ zu:
Die Punktanzahl $ n $ ist dabei immer einer mehr als die Anzahl der Teilstrecken, weil die Punkte ja die Teilstrecken begrenzen und daher ein zusätzlicher Punkt den Beginn oder den Abschluss bilden muss, jenachdem, wie wir drauf schauen.
Zur Berechnung der Koordinaten aller sich ergebenden Punkte $ r $ benutzen wir die natürlichen Zahlen von Null bis zum $ n $-ten Punkt mit Hilfe der entsprechenden Intervall-Menge $ [0, n] $ aus $ \mathbb{N} $.
Das Zählen
Die Erweiterung nach außen, die nach innen zurück wirkt
Beginnen wir noch einmal von vorne mit den Punkten Null und Eins.
Verdoppeln wir diese beiden Punkte, verschieben also den Punkt Null so auf die Eins, dass sich die Länge und Richtung der Verbindungsstrecke der neuen Punkte nicht verändert, dann schöpfen wir so den Punkt Zwei. Dies kommt, weil nun der verschobene Punkt der vorherigen Eins jetzt die Zwei bildet. Wir zählen damit also einen Punkt weiter zum Großen hin.
Wobei wir übrigens auch sehen, dass zwei aufeinander gelegte geometrische Punkte miteinander verschmelzen und zu einem werden, wie dies hier mit dem verdoppelten Nullpunkt geschieht, der nun auf der Eins liegt. Denn wir aber nun drei Punkte erhalten, die Null, die Eins und die Zwei, anstatt vier, wie naiv zu erwarten. Genau das war ja eingangs unser fundamentales Problem, das wir mit den Abständen und der fraktalen Befüllung der Lücken überwinden. Es zählen eben nur die Dinge, die wir unterscheiden können.
Mathematik beginnt dort,
wo wir das Eine vom Anderen unterscheiden können.
Ab da zählt alles.
Nehmen wir die entstandene Struktur und verkleinern sie gleichmäßig so, dass sie zwischen die Null und die Eins passt, dann erkennen wir, dass der mittlere Punkt die Strecke zwischen der Null und der Eins genau so teilt, wie wir dies Eingangs schon hatten – sie wird halbiert. Wir erhalten auch bei wiederholter Anwendung mit weiterer Verkleinerung und damit, diese immer wieder zwischen die Teilstrecken zu legen, keine Punkte, die wir nicht oben bei der Halbierung schon hatten. Beide Punktmengen sind von ihrer fraktalen Struktur her gleich, weil durch das halbieren und verdoppeln in beiden die reinen Potenzen von Zwei stecken.
Neue Teilungen durch weitere Primzahlen
Machen wir nun bei der Strecke Null, Eins und Zwei weiter und verlängern diese um einen weiteren Punkt,
wie zuvor, dann erhalten wir den Punkt Drei.
Wenn wir jetzt diese neue Struktur aus vier Punkten verkleinern und zwischen die Null und die Eins legen, dann erhalten wir eine Teilung, die ganz neue Punkte enthält. Nur die beiden Nullpunkte fallen zusammen und der neue Punkt Drei fällt nun auf die Eins. Alle anderen Punkte zwischen Null und Eins sind nicht doppelt, weil sie nicht auf die Punkte fallen, die durch die Halbierung beziehungsweise durch die Verkleinerung der Zweierstruktur auf die Strecke von der Null bis zur Eins entstanden waren.
Wir haben mit der Drei die nächste Primzahl nach der Zwei entdeckt, die ein neues Netzwerk oder Raster erzeugt. Auch dieses ist wieder in Bezug auf die Potenzen der Drei selbstähnlich. Denn wenden wir das gleiche Vorgehen wieder auf die durch die Dreiteilung entstandenen Teilstrecken an, dann entstehen tiefere fraktale Dreiteilungen, die sich durch Formeln so ausdrücken lassen:
Wenden wir die Dreiteilungen dann auch noch auf die Strecken der Halbierungen an, dann schöpfen wir zwei weitere Punkte, die wir noch nicht erreicht hatten, nämlich $ \frac{ 1 }{ 6 } $ und $ \frac{ 5 }{ 6 } $, die restlichen drei, $ \frac{ 2 }{ 6 } = \frac{ 1 }{ 3 } $, $ \frac{ 3 }{ 6 } = \frac{ 1 }{ 2 } $ und $ \frac{ 4 }{ 6 } = \frac{ 2 }{ 3 } $ hatten wir nämlich schon. Es ergibt sich:
Hierbei sind die Fraktalebenen $ x_{i} $ frei in ihrer Kombination.
Zählen wir nun, wie oben von der Zwei zur Drei, jetzt von der Drei zur Vier weiter und legen diese vier Teilstrecken wieder zwischen die Eins, dann erkennen wir, wie bei der Zwei, dass wir die Vierteilung, die 16-Teilung und so fort auch schon haben.
Das Zählen zur Fünf führt uns dann zur Fünfteilung zwischen der Null und Eins, wodurch die Primzahl Fünf uns nun sämtlich neue Punkte zwischen der Null und der Eins bringt. Auch die Kombination der Fünf mit den vorherigen Primzahlen Zwei und Drei bringt uns teils neue Punkte:
So geht es nun immer weiter.
Das komplette Raster oder Netzwerk aller ganzen negativen Primzahlpotenzen aufspannen
Die Sechs und ihre Sechsteilung haben wir schon komplett durch die Zwei-/Dreiteilung.
Die Sieben ist wieder eine neue Primzahl, die auch wieder mit allen vorherigen kombiniert werden kann.
Die Acht, die Neun und die Zehn haben wir schon durch die Zwei, Drei und Fünf.
Die Elf ist dann wieder eine neue Primzahl.
Dieses Vorgehen können wir nun immer weiter treiben:
Strecke wieder um Eins verlängern und durch skalieren überprüfen, ob wir eine neue Primzahl gefunden haben:
So bekommen wir das Teilernetz der Primzahlen und ihrer Kombinationen im Endlichen.
Alle Strecken der natürlichen Zahlen und schließlich der ganzen Zahlen vernetzen
Um diese Struktur auf alle natürlichen Zahlen auszudehnen, brauchen wir ein passendes Symbol:
Die Ordinalzahlen geben uns die Möglichkeit einen Wert auszudrücken, der so groß ist, dass er per Definition genau alle natürlichen Zahlen beinhaltet. Dieser aktual unendliche Wert hat das Symbol $ ω $ und bezeichnet die vollständige Induktion; die Zahl, die wir erreichen, wenn wir einmal alle natürlichen Zahlen gezählt haben.
Die zuvor gefundene feine Unterteilung können wir jetzt also mit Hilfe von $ ω $ zwischen alle jeweils benachbarten Zahlen legen
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { ω\;\;\;=\;\;\;\mathbb{N} } \] | (BO.Ein.NE.6) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \left( x_{i} \in \mathbb{N} \right) \left[\; n\;\;\;=\;\;\;\left( \prod_{\forall p_{i} \in \mathbb{P}} p_{i}^{x_{i}} \right) \cdot ω \;\right] } \] | (SN.ArGeo.21) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { d\;\;\;=\;\;\;\frac{ 1 }{ \prod_{\forall p_{i} \in \mathbb{P}} p_{i}^{x_{i}} }\;\;\;=\;\;\;\prod_{\forall p_{i} \in \mathbb{P}} p_{i}^{-x_{i}} } \] | (SN.ArGeo.22) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \left( \forall m \in [0, n]_{\mathbb{On}} \right) \left[\; r\;\;\;=\;\;\;\left( \prod_{\forall p_{i} \in \mathbb{P}} p_{i}^{-x_{i}} \right) \cdot m \;\right] } \] | (SN.ArGeo.23) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \rho\;\;\;=\;\;\;\prod_{\forall p_{i} \in \mathbb{P}} p_{i}^{x_{i}} \;\; , } \] | (SN.ArGeo.24) |
und das Ganze dann auch von der Null an in die negative Richtung immer weiter verlängern, mit der Basismenge $ \mathbb{On}_{0}^{\pm} $ der Intervall-Menge, wie im Abschnitt Die Menge der Ordinalzahlen ins Negative erweitert entwickelt,
In beiden Fällen fällt der Abschlusspunkt auf diese Weise bei $ n $ weg, weil die Zahl der Teilstrecken nicht endet. Der Abstand $ d $ und die Dichte $ \rho $ verändern sich nicht dadurch.
Dass es genau gleich viele negative Zahlen wie natürliche Zahlen, mit der Null, geben muss, sehen wir in den Biordinalzahlen.
Immer noch Lückenhaft
Die Kanten des geometrischen Netzgewebes besteht nun aus den Verbindungslinien der Punkte, wobei die Punkte die Knoten oder Stützen des Gewebes sind. Nehmen wir diese Teilungen der Strecken für jede der endlichen Primzahlen nur endlich oft vor, dann haben wir immer noch Lücken endlicher Größe.
Wie können wir aber die Lücken nun so schließen, dass sie keine endliche Größe mehr haben?
Übergang ins Unendliche
Die vollständige Induktion der Teilungen
Erst, wenn wir die Teilung der Strecken so bis ins Unendliche treiben, dass keine endlichen Lücken übrig bleiben, haben wir aus endlicher Sicht eine gewisse vollständige Lückenlosigkeit erreicht. Es dürfen dann auch keine unendlich kleinen Lücken verbleiben, in die wir mit endlichen Teilungen noch Punkte platzieren können, weil sie noch unbelegt sind.
Wie können wir nun erreichen oder ausdrücken, dass wir die Strecke zwischen Null und Eins wirklich in alle möglichen endlichen Potenzen der Primzahlen und deren Kombinationen aufteilen und so ein Teilernetz aufspannen, dass alle endlichen Teilungen beinhaltet?
Auch hierzu können wir das Symbol $ ω $ der Ordinalzahlen nutzen, nun als Potenz. Die Theorie der Ordinalzahlen kennt allerdings keine Vorgänger von $ ω $ und auch keine Vorgänger von Null, also auch keine negativen Zahlen. Diese Einschränkung haben wir mit der Theorie der Biordinalzahlen aufgehoben und können so auch den aktual unendlich negativen Wert $ -ω $ beschreiben, den wir in der Potenz unserer Primzahlen brauchen.
Für das Beispiel der Zweiteilung beziehungsweise Halbierung erhalten wir folgende Formeln, wenn wir die Teilung bis in die vollständige Induktion $ ω $ vorantreiben:
| ▾ | Notizen |
• Hier gehen wir davon aus, dass $ 2^{ω} $, und damit dann auch $ \left( 2^{ω} + 1 \right) + 1 = 2^{ω} + 2 $, wirklich einer geordneten Menge entspricht und vermutlich eine Ordinalzahl ist,
wofür ich noch keinen expliziten Beweis gesehen habe, was aber eine gewisse Plausibilität besitzt und hier so Verwendung findet, dass die Formeln in sich logisch erscheinen.
Die Fragestellung ist interessant und sollte auf der Seite der Biordinalzahlen untersucht werden.
Wir haben hier als Basismenge unserer Intervall-Menge $ \left( 2^{ω} + 1 \right) + 1 $ gewählt, weil in den Ordinalzahlen, wo wir hier davon ausgehen, dass $ 2^{ω} \in \mathbb{On} $, und so dann auch $ 2^{ω} + 1 $ und $ \left( 2^{ω} + 1 \right) + 1 $, eine solche ist, die Menge $ \left( 2^{ω} + 1 \right) + 1 $ dann auch die Zahl $ 2^{ω} + 1 $ als größte enthält, die wir ja für den Wert von $ n $ brauchen. Wir hätten hier dann auch $ \mathbb{On} $ als Basismenge nehmen können, aber so wird diese neue interessante Fragestellung auf diese Weise näher beleuchtet.
So erhalten wir zwar schon eine unendliche Dichte, denn der Abstand zwischen zwei benachbarten Netzpunkten $ d $ ist $ 2^{-ω} $, aber wie wir oben gesehen haben, sind hier ganz viele Teilungen noch nicht enthalten. Als Beispiele erreichen wir so die Punkte $ \frac{ 1 }{ 3 } $ und $ \frac{ 2 }{ 3 } $ nicht, die zu den rationalen Zahlen gehören. Ein aktual unendlich kleiner Abstand zwischen den Punkten reicht offenbar nicht aus, um alle durch endliche Teilungen zu beschreibenden Punkte zu erreichen.
Nehmen wir die Teilungen der Strecke zwischen Null und Eins für auch nur eine der endlichen Primzahlen gar nicht oder nur endlich oft vor, dann behalten wir Lücken, die zwar einen aktual unendlich kleinen Abstand aufweisen, aber in denen noch durch endliche Teilungen platzierbare, unbelegte Punkte existieren.
| ▾ | Notizen |
Kontinuumshypothese
• Hier stellt sich dann eben die Frage, ob die Mächtigkeit von beispielsweise $ 2^{ω} \cdot 3^{ω} $ oder gar dem nachfolgend definierten $ \s $ wirklich $ 2^{ω} $ ist. Wenn nicht, würde dies die verneinen.
Das aktual unendlich dichte Raster oder Netzwerk aller ganzen negativen Primzahlpotenzen aufspannen
So müssen wir also die Teilung mit allen endlichen Primzahlen bis in die vollständige Induktion
vorantreiben:
So gibt es nun zwischen Null und Eins keine rationalen Zahlen mehr, die von dem sich ergebenden Raster oder Netzgewebe nicht geschöpft werden.
Nun erweitern wir dieses Gewebe wieder auf alle ganzen Zahlen:
Auch hier fällt der Abschlusspunkt $ n $ wieder weg, weil die Zahl der Teilstrecken nicht endet. Der Abstand $ d $ und die Dichte $ \rho $ verändern sich dadurch nicht.
Können wir nun davon sprechen, dass ein solches Gewebe dann keine durch endliche Teilungen erreichbaren Lücken mehr hat?
Irrationale algebraische Zahlen
Gibt es noch Lücken im Gewebe?
Wir kennen in der Arithmetik mit den vier Grundrechenarten und dem Ziehen ganzer Wurzeln, inklusive dem Integrieren, noch die irrationalen algebraischen Zahlen, die allesamt mögliche Lösungen der Nullstellen von Polynomen darstellen.
Sind Zahlen, wie die zweite Wurzel aus Zwei $ \sqrt{2} $, im Raster enthalten?
Unser Beweis der Überrationalitätsvermutung
mit den auf ihm aufbauenden, nachfolgenden Beweisen(Link) zeigt,
dass die Radikale der irrationalen algebraischen Zahlen bereits im Raster enthalten sind,
wenn wir mit den Teilungen und damit auch mit den negativen Potenzen der Abstände ins Aktual-Unendliche übergehen.
Die Radikale der irrationalen algebraischen Zahlen sind die irrationalen algebraischen Zahlen, die durch die vier Grundrechenarten und dem Ziehen ganzer Wurzeln ausgedrückt werden können.
Nur für solche irrationalen algebraischen Zahlen, die dann noch durch Integration von Radikalen der irrationalen algebraischen Zahlen entstehen, können wir noch nicht Beweisen, dass sie auf dem Raster liegen. Das sie auf dem Raster liegen, liegt nahe, weil es sich um Summen von Wurzelausdrücken handelt, wo wir es für eine endliche Anzahl von Summanden schon bewiesen haben. Daher ist es auch für eine aktual unendliche Anzahl von Summanden zu vermuten.
Das es dennoch bisher unbewiesen ist, liegt daran, dass wir die Ableitung und das Integral mit Hilfe der Superial-Zahlen anders definieren, als bisher mit dem Limes üblich, und dadurch aktual unendlich kleine Summanden in die Integration bekommen, die sich an dieser Stelle dann zu Null summieren müssen, um im Ergebnis rein endlich zu sein. Durch die aktual unendlich kleinen Summanden haben wir mehr Genauigkeit zu berücksichtigen und erreichen so auch eine höhere Güte. Dadurch wird der Beweis aber auch schwieriger zu führen, was ihn bisher verhindert.
Warum ist nun zum Beispiel die zweite Wurzel aus Zwei $ \sqrt{2} $ schon ein Punkt des Rasters?
Dies kommt nach dem Beweis durch den Übergang der Potenz ins ganzzahlige Aktual-Unendliche.
Er zeigt, dass die Wurzel aus Zwei erst mit aktual unendlich großem Nenner und Zähler
als Bruch aus ganzen Zahlen dargestellt werden kann:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \left| \sqrt{ 2 } \right|\;\;\;=\;\;\;2^{\frac{ 1 }{ 2 }}\;\;\;=\;\;\;\frac{ 2^{ω} \cdot 2^{\frac{ 1 }{ 2 }} }{ 2^{ω} } } \] | (SN.ÜV.28) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}2^{\frac{ 1 }{ 2 }}\;\;\;=\;\;\;\frac{ 2^{ω + \frac{ 1 }{ 2 }} }{ 2^{ω} } \;\; , } \] | (SN.ÜV.29) |
wobei $ ω $ ein transfiniter Wert ist und nach unseren Axiomen gilt
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \left( \forall q \in \mathbb{Q} \setminus \left\{ 0 \right\} \right) \left[\; ω + q\;\;\;\raise{-.14ex}{᠄}\mspace{-4.5mu}\neq\;\;\;ω \;\right] \;\; . } \] | (SN.ÜV.30) |
Dieser Zusammenhang erscheint auf den ersten Blick eher banal. Denn der Faktor $ 2^{ω} $ ist offensichtlich sowohl im Nenner als auch im Zähler des Bruchs vorhanden und könnte deshalb natürlich direkt gekürzt werden. Womit wir auch sofort erkennen, dass die Formel wahr ist.
Was macht die Formel dann auf den zweiten Blick so besonders?
Bei genauer Betrachtung ist das Besondere, dass nur in einer solchen Form auch der Zähler zu einer ganzen Zahl wird. Denn der dem Beweis zugrunde liegende Widerspruch zeigt, dass kein Bruch aus endlichem ganzzahligen Nenner und endlichem ganzzahligen Zähler die Wurzel aus Zwei darstellen kann. Der Widerspruchsbeweis offenbart eine Konstruktionsanweisung, wie ein Bruch aus ganzen Zahlen beschaffen sein muss, der diese Zahl darstellen kann:
Der Bruch muss in diesem Fall beliebig endlich häufig mit Zwei zu kürzen sein. Was bedeutet, dass sowohl der Nenner als auch der Zähler aktual unendlich groß sein müssen. Der gefundene Bruch hat einen aktual unendlich großen ganzzahligen Nenner und ist offensichtlich wahr. Und er ist beliebig endlich oft mit Zwei zu kürzen. Bleibt die Frage, ob auch der Zähler eine aktual unendlich große ganze Zahl sein kann. Und dies ist mit einem klaren Ja zu beantworten. Denn der Widerspruchsbeweis ist so angesetzt, dass er einen ganzzahligen Zähler zur Bedingung macht und erst diese und weitere Annahmen die Konstruktionsanweisung hervorbringen.
Der Faktor $ 2^{ω} $ ist so groß – eben aktual unendlich groß –, ganzzahlig und so strukturiert, dass er im Produkt mit jeder ganzen Wurzel aus Zwei, also aus jeder rational gebrochenen Potenz von Zwei, eine ganze Zahl hervorbringt. Das ist die Besonderheit dieses Bruchs, die sofort unsichtbar wird, wenn wir einfach komplett kürzen. Sein Geheimnis wird erst offenbar, wenn wir seine Entstehungsgeschichte verstehen und damit seine Bedeutung entschlüsseln und so erkennen.
Oben in Formel haben wir berechnet, in welchem Abstand die Punkte auf dem aktual unendlichen Zweiteilungsraster liegen, nämlich $ d = 2^{-ω} $, wenn wir in die aktuale Unendlichkeit der vollständigen Induktion $ ω $ übergehen. Wir können diesen Abstand oder dieses Raster durch Skalierung, also durch Multiplikation, mit seinem Kehrwert $ 2^{ω} $, auf den Zählabstand von Eins bringen, also auf die Ganzzahligkeit:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { d\;\;\;=\;\;\;2^{-ω} \cdot 2^{ω}\;\;\;=\;\;\;1 } \] | (SN.ArGeo.37) |
Hier fällt nun auf, dass der Faktor exakt der gleiche ist, der aus der Wurzel aus Zwei vorstehend eine ganze Zahl macht; sie also auf dem Zählraster landet. Damit ist bestätigt, dass die Wurzel aus Zwei, also $ 1,\!41421356237309\cdots $, wirklich auf dem aktual unendlichen Zweiteilungsraster liegt.
Dies gilt für alle Wurzeln aus Zwei und deren Potenzen $ \left| \sqrt[k]{2} \right|^{m} $
Der Beweis zeigt, dies gilt für alle Wurzeln aus Zwei, die wir nachfolgend als Potenzen von Zwei schreiben:
Der Abstand des Rasters bleibt hier der gleiche, wie zuvor, und so auch der Faktor $ 2^{ω} $, um $ 2^{q} $ zu einer ganzen Zahl zu machen.
Dies gilt sogar für alle Wurzeln aus natürlichen Zahlen und deren Potenzen $ \left| \sqrt[k]{c} \right|^{m} $
Der Beweis zeigt dies sogar für jede Wurzel aus jeder natürlichen Zahl $ c $ und deren Potenzen wie folgt:
Hier ist zu bemerken, dass die Potenzen der Primzahlen der Primfaktorzerlegung von $ c $ ja größer als Eins sein können. Wenn zum Beispiel $ c = 4 = 2^{2} $ ist, dann ist $ c^{ω} = 4^{ω} = \left( 2^{2} \right)^{ω} = 2^{2 ω} $ und damit eine aktual unendliche Größenordnung größer als $ 2^{ω} $, wie oben zuvor.
Da stellt sich die Frage: Ist es wirklich notwenig die Größenordnung derart zu vergrößern? Oder reicht auch die einfache aktual unendliche Größe $ 2^{ω} $ aus? Dies ist eine besonders interessante und wichtige Frage in Bezug auf die Superial-Zahlen, weil es entscheidet, ob Produkte zwischen der superialen Basis $ \s $ und den Wurzeln aus $ c $ auch schon ganze Zahlen ergeben, wenn $ c $ größere Potenzen von Primzahlen enthält.
Dass die kleinere Größenordnung tatsächlich schon ausreichend ist, sehen wir an folgender Herleitung mit beliebigen natürlichen Potenzen $ k $ von Primzahlen $ p $:
Wir sehen: Wenn die Potenz $ ω $ einer Primzahl $ p $ mal $ p $ hoch jeder rationalen Zahl $ q $ eine aktual unendliche ganze Zahl ergibt, dann ist $ k \cdot q $ einfach eine andere rationale Zahl, die als Potenz von $ p $ ebenso eine ganze Zahl ergeben muss. Und dies gilt schließlich für alle endlichen Potenzen der Primzahlen der Primfaktorzerlegung jeder positiven natürlichen Zahl $ c $.
Wenn $ \rad(c) $ das Produkt der in $ c $ enthaltenen Primzahlen in einfacher Potenz ist, also beispielsweise
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \rad(980)\;\;\;=\;\;\;\rad(2^{2} \cdot 5 \cdot 7^{2})\;\;\;=\;\;\;2 \cdot 5 \cdot 7\;\;\;=\;\;\;70 \;\; , } \] | (SN.ArGeo.49) |
können wir also formulieren, dass schlussendlich jede endliche ganze Wurzel in natürlicher Potenz aus jeder natürlichen Zahl $ c $ durch ein Produkt aller unterschiedlichen Primzahlen in $ c $ zu einer aktual unendlich großen ganzen Zahl gemacht werden kann:
Jede endliche ganze Wurzel in natürlicher Potenz aus jeder natürlichen Zahl $ c $ kann also entsprechend als überrationaler Bruch zweier aktual unendlich großer ganzer Zahlen dargestellt werden:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}c^{q}\;\;\;=\;\;\;\frac{ \rad(c)^{ω} \cdot c^{q} }{ \rad(c)^{ω} } } \] | (SN.ArGeo.51) |
Dies ist sehr bemerkenswert und lässt uns einige neue Erkenntnisse in der Zahlentheorie und bezüglich der arithmetischen Struktur der Geometrie gewinnen. Es zeigt uns, auf welche Weise die Wurzeln in das fraktale Teilungsgewebe der Geometrie eingewoben sind.
Wie oben erwähnt, gilt dies für alle Radikale der irrationalen reell algebraischen Zahlen, was wir ja an anderer Stelle zeigen, also für deren Summen, Produkte, Brüche und endlichen ganzzahligen Potenzen.
Die besondere Rolle der normierten Einheit $ ω $
Die aktual unendliche Einheit der vollständigen Induktion $ ω $ nimmt hier eine ganz besondere Rolle ein.
Mit Hilfe von $ ω $ können wir eine normierte aktual unendliche Potenz der Primzahlen ausdrücken, die es uns ermöglicht, das Fraktal der arithmetischen Teilung der Geometrie im Hinblick auf rein endliche Zahlen so zu vervollständigen, dass alle Radikale der irrationalen reell algebraischen Zahlen im geschöpften Raster enthalten sind, vermutlich sogar wirklich alle reell algebraischen Zahlen, also auch alle irrationalen in ihnen.
Dabei ist es vermutlich so, dass die transzendenten Zahlen aktual unendlich kleine Summanden enthalten, die dafür sorgen, dass sie nicht zu den rein endlichen Zahlen dazugehören, wie wir bereits an der eulerschen Zahl $ \e_{\s} $ zeigen konnten.
Noch außergewöhnlicher wird die Rolle von $ ω $, wenn wir im Beweis der Primzahlprodukt-Vermutung sehen, dass $ ω $ – also die vollständige Induktion selber – eine Primfaktorzerlegung in Form des Produkts aller endlichen Primzahlen besitzt.
Die superiale Basis $ \s $ wird auf natürliche Weise sichtbar und definiert
Das aktual unendliche Fraktal der arithmetischen Teilung der Geometrie basiert also auf einem Produkt der aktual unendlichen Potenz aller endlichen Primzahlen, der superialen Basis $ \s $, auf dem die vorliegende Arbeit gegründet ist:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \s\;\;\;≔\;\;\;\displaystyle \prod_{\forall n \in \mathbb{N}} \left( \prod_{\forall p \in \mathbb{P}} p \right) } \] | (SN.Ein.24) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\s\;\;\;≔\;\;\;\displaystyle \left( \prod_{\forall p \in \mathbb{P}} p \right)^{ω} } \] | (SN.Ein.26) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\s\;\;\;=\;\;\;ω^{ω} } \] | (SN.PP.174) |
Eine ZFC-konforme Definition der Eigenschaften unseres unendlichen Produkts der superialen Basis $ \s $ über $ p $-adische Bewertungen findet sich auf der Seite ›Die ZFC-Modellkonstruktion der Superial-Zahlen‹.
Als Teilung der Eins ist es dann die Zahl $ \s^{-1} $, die der Strecke zwischen Null und Eins unsere vorstehend gefundene arithmetische Struktur gibt, indem sie für die normierte aktual unendlich kleine Distanz steht:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { n_{\s}\;\;\;=\;\;\;\s + 1 } \] | (SN.ArGeo.52) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { d_{\s}\;\;\;=\;\;\;\frac{ 1 }{ \s }\;\;\;=\;\;\;\s^{-1} } \] | (SN.ArGeo.53) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \left( \forall m \in [0, n_{\s}]_{\mathbb{S}_{\Z}} \right) \left[\; r_{\s}\;\;\;=\;\;\;\s^{-1} \cdot m \;\right] } \] | (SN.ArGeo.54) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \rho_{\s}\;\;\;=\;\;\;\s } \] | (SN.ArGeo.55) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \# \mathbb{Z}\;\;\;=\;\;\;2 ω } \] | (BO.Ein.NE.7) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}n_{\s,\Z}\;\;\;=\;\;\;2 ω \cdot \s } \] | (SN.ArGeo.56) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}\left( \forall m \in \;]\!-\!ω \cdot ω^{ω}, ω \cdot ω^{ω}[_{\mathbb{On}_{0}^{\pm}} \right) \left[\; r_{\s,\Z}\;\;\;=\;\;\;ω^{-ω} \cdot m \;\right] } \] | (SN.ArGeo.57) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\left( \forall m \in \;]\!-\!ω \cdot \s, ω \cdot \s[_{\mathbb{On}_{0}^{\pm}} \right) \left[\; r_{\s,\Z}\;\;\;=\;\;\;\s^{-1} \cdot m \;\right] } \] | (SN.ArGeo.58) |
Dabei bezeichnet $ n_{\s} $ die Anzahl aller Punkte des normierten aktual unendlich feinsten Gewebes im Endlichen von Null bis einschließlich Eins. $ d_{\s} $ beschreibt den Abstand dieser feinsten Punkte und $ \rho_{\s} $ ihre Dichte. $ n_{\s,\Z} $ ist dann die Anzahl der feinsten Punkte auf der endlichen Zahlengeraden, unter Berücksichtigung der Tatsache, dass es dann keinen Abschlusspunkt braucht.
So erreichen wir das feinste Gewebe von Punkten, die auf diese Weise nur ganze Zahlen in ihren aktual unendlich kleinen Summanden, in ihrem Ort – ihren Koordinaten – haben, aber doch normiert aktual unendlich dicht beieinander liegen.
Die Abgeschlossenheit der Teilung der Strecke Eins in $ \s $ Teile
Eine Besonderheit in Bezug auf $ \s $ und die Adressierung der superial kleinen ganzen Zahlen $ \mathbb{S}_{\Z}^{-1} $ von Null bis ohne Eins
Wenn wir die Strecke zwischen Null und Eins in $ \s $ Teile teilen, dann ist jedes Teil $ \s^{-1} $ groß.
Adressieren wir die Punkte, die zwischen den Teilen sind, dann beginnen wir mit Null, dann $ \s^{-1} $,
$ 2 \s^{-1} $, $ 3 \s^{-1} $ und so fort.
Doch was passiert, wenn wir über die endlichen natürlichen Faktoren $ n \cdot \s^{-1} $ hinaus gehen?
Da wir die Punkte der Strecke zwischen Null und Eins adressieren wollen, sollten wir an allen entsprechenden Zahlen zwischen Null und Eins vorbeikommen, wie $ \frac{ 1 }{ 3 } $, $ \frac{ 1 }{ 2 } $ oder $ \frac{ 2 }{ 3 } $, die nichts anderes sind als $ \frac{ 1 }{ 3 } \s^{1} \s^{-1} $, $ \frac{ 1 }{ 2 } \s^{1} \s^{-1} $ oder $ \frac{ 2 }{ 3 } \s^{1} \s^{-1} $. Und Zahlen wie $ \frac{ 1 }{ 3 } \s^{1} \s^{-1} - 2 \s^{-1} $, $ \frac{ 1 }{ 3 } \s^{1} \s^{-1} - \s^{-1} $ oder $ \frac{ 1 }{ 3 } \s^{1} \s^{-1} + \s^{-1} $, $ \frac{ 1 }{ 3 } \s^{1} \s^{-1} + 2 \s^{-1} $ sollten auch dazu gehören. Also alle Zahlen, die zwischen Null und Eins liegen und aktual unendlich kleine und dort ganze Zahlen sind. Deshalb müssen alle $ a \cdot \s^{1} \s^{-1} = a \cdot \s^{0} = a $ mit $ a \in \mathbb{A}_{\S} $, also vom aktual unendlich Kleinen aus gesehen die $ a \cdot \s^{1} $, auch aktual unendlich kleine ganze Zahlen sein, die von dort aus halt nur als aktual unendlich Groß erscheinen. Denn die Summe einer dort ganzen Zahl $ z \cdot \s^{-1} $ mit $ z \in \mathbb{Z} $ ergibt nur mit einer anderen ganzen Zahl $ a $ wieder eine aktual unendlich kleine ganze Zahl $ a + z \cdot \s^{-1} $.
Aus diesem Grund müssen alle $ a \in \mathbb{A}_{\S} $ im aktual unendlich Kleinen, in der Größenordnung $ \s^{-1} $, auch immer ganze Zahlen sein. Skaliert auf endliche ganze Zahlen müssen dann alle $ a \cdot \s $ mit $ a \in \mathbb{A}_{\S} $ in der Größenordnung des Endlichen auch immer rein ganze Zahlen sein, wenn auch aktual unendlich groß.
Nun bekommen wir eine im ersten Moment vielleicht paradox erscheinende Situation:
Wir haben von der Null an bis direkt vor die Eins $ \s $ aktual unendlich kleine ganze Zahlen. Für jeden endlichen Faktor $ a $ vor $ \s^{0} $, also $ a \cdot \s^{0} = a \cdot \s^{1} \s^{-1} $, laufen aber $ 2 ω $ ganzzahlige Zahlen des Summanden $ z \cdot \s^{-1} $ durch. Zusammen also $ a + z \cdot \s^{-1} $, wobei bei Null nur $ 0 + n \cdot \s^{-1} $, mit $ n \in \mathbb{N} $, und bei Eins nur $ 1 + z^{-} \cdot \s^{-1} $, mit $ z^{-} \in \mathbb{Z}^{-} $. Damit enthält die Menge $ \lbrack 0, 1 \lbrack_{\mathbb{A}_{\S}} $ der Koeffizienten der Superial-Zahlen $ \# \lbrack 0, 1 \lbrack_{\mathbb{A}_{\S}} = \frac{ \s }{ 2 ω } $ Elemente, wie wir auch in Formel SN.Ei.S.L.11 sehen.
Wir haben hier die Besonderheit, wie auch noch im Abschnitt ›Die superiale Basis $ \s $ hat bezüglich der Struktur des Aktual-Unendlichen eine bemerkenswerte doppelte Bedeutung‹ genauer beleuchtet wird, dass eine Teilung der Strecke zwischen Null und Eins in $ \s $ Teile in Punkte zwischen den Teilen mündet, deren Koordinaten nur durch Summen ausgedrückt werden können, die im Allgemeinen aktual unendlich kleine Summanden enthalten. Und dies, obwohl die Teilung eigentlich aus einer unendlichen Teilung, und damit aus einem Produkt mit unendlich kleinem Faktor, hervorgeht. Dies kann im ersten Moment sonderbar erscheinen.
Erst die Kombination der aktual unendlich kleinen Summanden und den endlichen Summanden mit Elementen aus $ \mathbb{A}_{\S} $ macht es wieder rund und gibt uns einen tiefen und außergewöhnlichen Einblick in die Zahlentheorie allgemein und im Besonderen in einen weiteren Zusammenhang zwischen Primzahlen, natürlichen, ganzen, rationalen und algebraischen Zahlen sowie deren Verbindung über die Ordinalzahlen und die Biordinalzahlen, was in meinen Augen sehr besonders ist.
So können wir die Abgeschlossenheit der Teilung der Strecke von Null bis Eins durch $ \s $ erkennen. Durch diese Teilung kommen wir von der Eins genau eine Fraktalebene tiefer bei der Eins auf Ebene $ \s^{-1} $ heraus, bei den aktual unendlich kleinen ganzen Zahlen. So sehen wir, dass eine weitere Teilung nichts wirklich neues ergibt, außer, dass sich die Struktur wiederholt, bis wir abermals bei einer noch kleineren Eins auf Ebene $ \s^{-2} $ herauskommen.
Das Kontinuum
Das Gewebe der Teilung durch $ \s $ bildet so in gewisser Hinsicht einen Abschluss in der vollständigen endlichen Teilung, wie eben erklärt, durch die es keine endlichen Abstände mehr gibt und keine Punkte, die durch endliche Teilung, selbst in Potenz der vollständigen Induktion, noch unbelegt oder unerreicht sind.
Wenn Kontinuum bedeutet, dass wir keine aktual unendlich kleinen Summanden in den Adressen der Zahlengerade haben wollen
Weil nun nach Formel SN.Ei.S.L.11 die Anzahl der sinnvollen
Koeffizienten der Superial-Zahlen von der Null bis vor die Eins $ \# \lbrack 0, 1 \lbrack_{\mathbb{A}_{\S}} = \frac{ \s }{ 2 ω } $ ist, wie geschildert,
und es in allen Koeffizienten, also auf der Zahlengeraden mit rein endlichen Adressen, dieses Intervall $ 2 ω $ mal gibt, wie wir im Abschnitt ›Erklärung der Anzahl der endlichen ganzen Zahlen durch ihren ontologischen Ursprung in der Struktur der Biordinalzahlen‹
lernen, dann muss es insgesamt $ \# \mathbb{A}_{\S} = \# \lbrack 0, 1 \lbrack_{\mathbb{A}_{\S}} = \frac{ \s }{ 2 ω } \cdot 2 ω = \s $ Koeffizienten geben.
Es gilt also $ \# \mathbb{A}_{\S} = \s $. Damit ist die mögliche maximale Teilung der Zahlengeraden mit rein endlichen Adressen dann erreicht und abgeschlossen, wenn wir sie in $ \s $ Teile teilen. Dies würde ich als erreichen des Kontinuums bezeichnen.
Klar ist aber, dass dieses Gewebe im Hinblick auf seine Stützpunkte immer lückenhaft bleibt. Denn wir können superial kleine Summanden zu den Adressen – gemeint sind Positionen oder vielleicht auch Koordinaten – hinzufügen und sowie auch oder die Potenzen der endlichen Teilungen natürlich immer weiter treiben, hin zur quadratischen normierten vollständigen Induktion der Potenz aller Primzahlen $ \s^{2} $ und weit darüber hinaus, womit wir immer mehr Punkte zwischen den schon adressierten erreichen. Jedoch handelt es sich dann nicht mehr um rein endlich adressierbare Punkte, die einfache normierte vollständige Induktion; eben nicht mehr die erste Norm.
Deshalb ist in diesem Sinn mit der Teilung der Zahlengeraden durch $ \s $ das Kontinuum erreicht. Aber Kontinuum bedeutet eben nicht, dass es keinerlei Lücken mehr gibt; halt nur keine, die durch endliche Primzahlen in endlicher Potenz oder in Potenz der einfachen normierten vollständigen Induktion erreichbar sind.
Demnach ist das Kontinuum so etwas wie $ \mathfrak{c} \overset{?}{=} \# \mathbb{A}_{\S} = \s = 2^{ω} \cdot 3^{ω} \cdot 5^{ω} \cdot 7^{ω} \cdot 11^{ω} \cdot 13^{ω} \cdot 17^{ω} \cdot 19^{ω} \cdot 23^{ω} \cdot \cdots $. Das könnte bedeuten $ \mathfrak{c} \ne 2^{ω} $.
Dies ist jedoch eine andere Definition des Kontinuums als über die Mächtigkeit, wo $ \left| \mathbb{A}_{\S} \right| = ω $ wäre, weil $ \mathbb{A}_{\S} $ abzählbar viele Elemente besitzt. Wir sehen, die Superial-Zahlen machen eine Reflexion der Bedeutung und Definition des Kontinuums notwendig.
Die zwei Konstruktionen von $ \s $
Es lassen sich mindestens zwei geometrische Konstruktionen finden, die der über das unendliche Primzahlprodukt aus der Einleitung äquivalent sind:
Die erste der folgenden Konstruktionen geht ins aktual unendlich Große und die zweite ins aktual unendlich Kleine. Beide definieren $ \s $ jedoch auf etwas unterschiedliche Weise:
Definition von $ \s $ über den Wiederholungsrhythmus der natürlichen Zahlen
|
In der geometrischen Konstruktion der rhythmischen Wiederholung bleiben die Begrenzungspunkte der Teilstrecken immer im selben Abstand von Eins. Am jeweiligen Ende der Punktreihe werden stets die nötigen Punkte angehängt, um den Rhythmus der nächsten natürlichen Zahl zu integrieren, wenn er noch nicht enthalten sein sollte (siehe ).
Definition von $ \s^{-1} $ über den Regen der natürlichen Zahlen
|
In der Konstruktion der rhythmischen Zerlegung werden zwischen den vorhandenen Begrenzungspunkte der Teilstrecken immer neue Punkte hinzugefügt, um den Rhythmus der hinzukommenden natürlichen Zahl in einem gleichmäßigen Rhythmus zu integrieren, falls er noch nicht vorhanden ist (siehe ).
Dies ist, als wenn ein Regen von natürlichen Zahlen auf der Strecke der Eins herniedergeht.
Explizites Primzahlflächenprodukt von $ \s $
Für das Primzahlprodukt von $ \s $ ergibt sich in beiden Fällen eine mit unendlich mal unendlich vielen Primzahlen gefüllte Fläche
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \s\;\;\;=\;\;\;\prod_{\forall n \in \mathbb{N}} \left( 2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 13 \cdot 17 \cdot 19 \cdot 23 \cdot \cdots \right) } \] | (SN.Ein.27) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\s\;\;\;=\;\;\;(2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 13 \cdot 17 \cdot 19 \cdot 23 \cdot \cdots )_{1} \\ \qquad\qquad\quad\; \cdot ( 2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 13 \cdot 17 \cdot 19 \cdot 23 \cdot \cdots )_{2} \\ \qquad\qquad\quad\; \cdot ( 2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 13 \cdot 17 \cdot 19 \cdot 23 \cdot \cdots )_{3} \\ \qquad\qquad\quad\; \;\;\;\; \vdots \\ \qquad\qquad\quad\; \cdot ( 2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 13 \cdot 17 \cdot 19 \cdot 23 \cdot \cdots )_{n \in \mathbb{N}} \\ \qquad\qquad\quad\; \;\;\;\; \vdots } \] | (SN.Ein.28) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\s\;\;\;=\;\;\;\left( 2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 13 \cdot 17 \cdot 19 \cdot 23 \cdot \cdots \right)^{ω} \;\;, } \] | (SN.Ein.29) |
wie wir sie oben schon definiert haben.
Wie wir aus Punkten eine Linie konstruieren können
Ein naturphilosophisches Problem gibt uns einen Einblick in die fraktale Realität der Geometrie
Kommen wir nun zu unserem fundamentalen Problem, eine Linie aus Punkten zu bilden beziehungsweise zu konstruieren, vom Anfang der Seite zurück und sehen, wie wir nun, nach unserer Erkenntnisreise, darauf Antworten können.
Stapelei – „Hochstapelei“ – ist nicht möglich, wie wir festgestellt haben, wenn ein geometrisches Element, wie ein Punkt, keine Ausdehnung hat. Wir können auch sagen, haben geometrische Elemente keine Struktur, und damit keine Ausdehnung, sind sie unteilbar, dann können wir sie nicht so miteinander verbinden, dass sie gemeinsam mehr sind als ihre Einzelteile. Es können also keine wirklich unteilbaren Atome sein, wenn wir sie stapeln möchten.
Ein Punkt muss also eine Struktur im Sinne einer Umgebung besitzen, die ihm eine Ausdehnung verleiht. Und genau diese Struktur liefert uns die oben untersuchte arithmetische Struktur der Geometrie über ihre Teilbarkeit durch Primzahlen und der sich daraus ergebenden superialen Basis $ \s $. Durch die Superial-Zahlen bekommt ein Punkt im endlichen eine Umgebung der Struktur $ a \cdot \s^{-1} $ mit $ a \in \mathbb{A}_{\S} $.
|
In sehen wir, dass jeder Punkt im Endlichen der Ebene oder Potenz $ \s^{0} $, hier am Beispiel von $ -1,\!4 \, \s^{0} = -1,\!4 $, als Umgebung einen ganzen Zahlenstrahl auf Fraktalebene $ \s^{-1} $ hat. Der Zahlenstrahl um jeden Punkt hat so dann die Ausdehnung $ 2 ω \, \s^{-1} $, weil der Koeffizient $ a $ über alle ganzen Zahlen läuft und die Anzahl der ganzen Zahlen $ \# \mathbb{Z} = 2 ω $ ist.
Verbinden wir $ \frac{ \s }{ 2 ω } $ Punkte dieser Struktur, dann erhalten wir eine Strecke der Länge $ 1 $. Verbinden wir $ \s $ Punkte dieser Struktur, dann erhalten wir den ganzen Zahlenstrahl von minus Unendlich $ -ω $ bis plus Unendlich $ ω $.
Eine fraktale Struktur der geometrischen Elemente löst das Problem mit Punkten eine Linie, mit Linien eine Fläche und mit Flächen ein Volumen zu beschreiben. Und genau dies ist ja ganz eng mit dem Thema der Integration oder allgemeiner mit der Differenzialrechnung verbunden. Es ist also kein Zufall, dass wir über die Superial-Zahlen auf die arithmetische Struktur der Geometrie stoßen, in der sich dann die Superial-Zahlen als Zahlentheorie der Analyses widerspiegeln.
| → |
|
Die Ontologie der Geometrie |
|
Eine Diskussion – ein Versuch der Annäherung
| ← |
Wie können wir verstehen, was die Ontologie der Geometrie mit dem Unterschied zwischen reell algebraischen und transzendenten Zahlen zu tun hat?
Im simplen Fall reicht eine rein reell algebraische Geometrie aus
Kurz und knapp – vielleicht auch etwas zu verkürzt - würde ich sagen, um simple geometrische Strukturen abzubilden brauchen wir zunächst keine transzendenten Zahlen. Die arithmetische Struktur der Geometrie, die wir oben herausgefunden haben und von der wir vermuten, dass deren Koeffizienten der Superial-Zahlen tatsächlich reell algebraisch sind, und nicht nur solche, die durch Radikale darstellbar sind, legt nahe, dass die Koordinaten der Grundstruktur der Geometrie mit reell algebraischen Zahlen auskommt. In diesem Fall sind dann keine Koordinaten notwendig, die unendlich kleine Summanden beinhalten, wie es demnach offenbar bei transzendenten Zahlen der Fall ist.
Wenn wir also für einfache Relationen erst einmal mit reell algebraischen Koordinaten auskommen, dann sind nicht nur die Parameter, sondern auch die Koordinaten der Relationen von Geraden, Parabeln, allgemein Polynomen, Vielecken und selbst Kreisen oder Ellipsen allesamt ebenfalls reell algebraische Zahlen, wenn eine der beiden Koordinaten, der Mittelpunkt und der Radius ebenfalls reell algebraisch sind; vielfach sogar solche, die durch Radikale – also Wurzeln - darstellbar sind.
Für die Kreisrelation stellt es sich so dar:
Das bedeutet bei diesen einfachen Geometrie können wir mit reell algebraischen Eingabeparametern und reell algebraischen Ergebniskoordinaten auskommen. Und auch elliptische Kurven kommen unter bestimmten Umständen mit reell algebraischen Koordinaten aus, und in jedem Fall mit algebraischen Koordinaten.
Wir können die oben angeführten Kurven (Funktionen) auch rotieren oder anderweitig mit Matrizen aus reell algebraischen Zahlen verschieben, spiegeln oder verzerren – multiplizieren –, die Ergebniskoordinaten bleiben reell algebraische Zahlen. Das auf dieser Seite eingangs gefundene Raster gibt uns die Möglichkeit ein Quadrat um 45° – $ ½π $ – zu drehen und die Koordinaten seiner Eckpunkte liegen immer noch auf diesem Raster, weil sie durch Radikale – in diesem Fall zweite Wurzeln – darstellbar sind.
Exponentialfunktionen mit einer ganzzahligen oder rationalen Basis sind allerdings auf diesem Raster nur darstellbar, wenn wir uns auf rationale Eingangsparameter beschränken. Das entspricht aber nicht der hier anvisierten Geometrie, in der die Eingangswerte und Ergebniswerte aus der selben Zahlenmenge, nämlich der gefundenen arithmetischen Struktur der Geometrie, vermutlich den reell algebraischen Zahlen, kommen sollen.
Wann kommen transzendente Zahlen ins Spiel?
Die transzendenten Zahlen kommen ins Spiel, wenn wir uns beispielsweise mit der Länge der Kurven beschäftigen oder zu den Exponentialfunktionen übergehen wollen.
Der Umfang eines Kreises $ 2π $ ist beispielsweise eine Länge oder Strecke entlang der Kreisrelation und eine transzendente Zahl.
(In Arbeit …)
Können wir einen Kreis entlang des Kreisumfangs so parametrisieren, dass wir nur rein reell algebraische Koordinaten erhalten?
Nutzen wir die $ \e $-Funktion zur Parametrisierung einen Kreises entlang seines Kreisumfanges mit reellen Zahl als Parameter, ist es völlig klar, dass diese auch transzendente Koordinaten liefert. Und zwar, weil die reellen Zahlen auch transzendente Zahlen enthalten:
Wenn $ \mathbb{T} $ die Menge der transzendenten Zahlen und $ \mathrm{Re}\left( c \right) $ der Realanteil der komplexen Zahl $ c $ ist.
Es kommt sodann die Frage auf, ob wir den Kreis auch so parametrisieren können, dass nur reell algebraische Zahlen im Real- und im Imaginäranteil herauskommen:
Und dies so, wie im vorstehenden Beispiel dadurch, dass wir zwar wegen des Faktors $ 2 π $ außer die Null nur transzendente Zahlen im Exponenten haben, diese aber über den Faktor $ a $ so granuliert sind, dass alle Ergebnisse auf dem Raster von $ \s^{-1} $ in der Menge der komplexen Zahlen $ \mathbb{C} $ liegen. Dabei möchte ich im Folgenden $ \mathbb{C}_{\S} $ als die Menge der komplexen Zahlen auf diesem Raster bezeichnen.
Nach den Erkenntnissen, die wir im Rahmen der Superial-Zahlen und ihrer arithmetischen Struktur der Geometrie haben, wissen wir, dass es $ \s $ algebraische Koeffizienten der Superial-Zahlen insgesamt gibt. Für den oberen Parameter $ a $ erhalten wir dann eine vollständige Kreisumrundung, wenn er von Null bis Eins durchläuft.
Nach unseren Erkenntnissen kommt die Nutzung des Faktors $ a $ der Teilung der Strecke Eins durch ganzzahligen Exponenten von Primzahlen im Eingangsabschnitt dieser Seite gleich, nur das hier der Kreisumfang beziehungsweise der Winkel entsprechend geteilt wird: Nehmen wir einfachheitshalber den Einheitskreis, dann ist in seine Punktmenge $ \mathbb{K}_{1} $ ohne Teilung die einzige Koordinate der Einheitsvektor auf der realen oder x-Achse:
(In Arbeit …)
Tabelle der Koordinatendreiecke für das 16-Eck
Jeder Punkt $ P_{k} $ liegt auf dem Einheitskreis bei:
Alle Koordinaten lassen sich durch Radikale, also Wurzelausdrücke, darstellen, wie ich vermutet habe:
(In Arbeit …)
Beweis: Die Koordinaten der Ecken eines regelmäßigen $ m $-Ecks sind algebraische Zahlen
Schritt 1: Darstellung der Ecken in komplexer Form
Die Eckpunkte eines regelmäßigen $ m $-Ecks auf dem Einheitskreis sind durch die komplexen Zahlen
gegeben. Diese Werte sind die $ m $-ten Einheitswurzeln, also die Lösungen der Gleichung
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { z^{ m }\;\;\;=\;\;\;1 \;\; . } \] | (SN.ArGeo.O.13) |
Die reellen Koordinaten der Ecken sind die Kosinus- und Sinuswerte:
Unsere Aufgabe ist es zu zeigen, dass $ x_{k} $ und $ y_{k} $ reell algebraische Zahlen sind, also Lösungen eines Polynoms mit ganzzahligen Koeffizienten.
Schritt 2: Minimalpolynom der Einheitswurzeln
Die Gleichung
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { z^{m} - 1\;\;\;=\;\;\;0 } \] | (SN.ArGeo.O.16) |
hat die Lösungen $ z_k = e^{2\pi i k / m} $, also genau die Ecken des $ m $-Ecks. Da dieses Polynom ganzzahlige Koeffizienten hat, folgt sofort, dass jede Einheitswurzel $ z_k $ eine algebraische Zahl ist. Tatsächlich sind die Einheitswurzeln die Nullstellen des sogenannten $ m $-ten Kreisteilungspolynoms:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Phi_{m}(z)\;\;\;=\;\;\;\prod_{\substack{1 \leq k \leq m \\ \gcd(k, m) = 1}} \left( z - e^{2\pi i k / m} \right) } \] | (SN.ArGeo.O.17) |
Wobei $ \gcd(k, m) $ (auch ggT genannt) die größte natürliche Zahl ist, durch die die beiden Zahlen $ k $ und $ m $ teilbar sind.
Dieses Polynom hat ganzzahlige Koeffizienten, was zeigt, dass jede Einheitswurzel $ e^{2\pi i k / m} $ eine algebraische Zahl ist.
Schritt 3: Kosinus und Sinus sind ebenfalls algebraisch
Da ja, wie oben beschrieben, gilt
(auf obere Formel verweisen, Nummerierung!)
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { z_{k}\;\;\;=\;\;\;e^{2\pi i k / m}\;\;\;=\;\;\;\cos \frac{2\pi k}{m} + i \sin \frac{2\pi k}{m} \;\; , } \] | (SN.ArGeo.O.18) |
und wir bereits gezeigt haben, dass $ z_k $ algebraisch ist, genügt es zu zeigen, dass auch Kosinus und Sinus algebraisch sind. Das folgt direkt aus den Identitäten
Da sowohl $ e^{i\theta} $ als auch $ e^{-i\theta} $ algebraische Zahlen sind – weil sie Einheitswurzeln sind –, folgt aus diesen Linearkombinationen, dass auch $ \cos \theta $ und $ \sin \theta $ algebraische Zahlen sind.
Schritt 4: Fazit
Da sich $ \cos \frac{2\pi k}{m} $ und $ \sin \frac{2\pi k}{m} $ als Linearkombinationen von Einheitswurzeln ausdrücken lassen
und Einheitswurzeln algebraische Zahlen sind, folgt:
Die Koordinaten aller Ecken eines beliebigen regelmäßigen $ m $-Ecks sind algebraische Zahlen.
Analyse des Beweises und Projektion der Bedeutung in der betrachteten Geometrie
Dies erscheint auf den ersten Blick recht erstaunlich, weil wir es ja bei der obigen exponentiellen $ \e $-Funktion, zur Beschreibung des Kreises, sowohl in der Basis als auch im Exponenten, bis auf beim Ausgangseckpunkt $ k = 0 $, nur mit rein transzendenten Zahlen zu tun haben. Diese neutralisieren sich hier aber vollständig in Bezug auf ihre Transzendenz.
Was passiert, wenn wir mit der Anzahl der Ecken ins Unendliche übergehen?
Abschätzung der Anzahl an Ecken, die algebraische Koordinaten haben können
In Bezug auf die Kreisrelation des Einheitskreises, die wir weiter oben betrachtet haben, kann sowohl die $ x $-Koordinate als auch die $ y $-Koordinate
alle algebraischen Zahlen zwischen minus Eins und plus Eins annehmen, nur nicht in freier Kombination.
Wenn $ x $ von minus Eins bis plus Eins durchläuft, dann treten, außer an den Scheitelpunkten, immer zwei verschiedene $ y $-Koordinaten auf,
und zwar in der Kombination $ \pm y $.
Wir haben es also mit der Anzahl $ 2 \cdot \# ( \lbrack -1, 1 \rbrack_{\mathbb{A}_{\R}} ) - 2 $ zu tun. Dies sind viel mehr Koordinaten, als wir sie durch ein regelmäßiges $ m $-Eck bekommen können, denn dies wären durch vollständige Induktion nur $ ω $ viele Koordinaten. Die unterschiedlichen $ m $-Ecke enthalten eben unterschiedliche Koordinaten, je nach der Primfaktorzerlegung von $ m $, sodass wir durch alle $ ω $ $ m $-Ecke kombiniert eine Anzahl von $ \s $ Koordinaten erhalten. Dies ist nicht anders, als bei der Teilung der Strecke von Null bis Eins, wie oben entwickelt und hätte nach meiner Ansicht zur Folge, dass die Koordinaten überwiegend superial kleine Summanden bekämen.
Der obige algebraische Parameter $ a $ der Eingangs formulierten $ \e $-Funktion für den Einheitskreis enthält allerdings nicht $ \s $ viele Möglichkeiten bereit. Er läuft nur von $ \lbrack 0, 1 \lbrack_{\mathbb{A}_{\R}} $, wenn die Koordinaten keine Dopplung haben sollen.
Nehmen wir an es gilt unsere Vermutung $ \mathbb{A}_{\S} \overset{?}{=} \mathbb{A}_{\R} $: Dann wäre $ \# ( \lbrack 0, 1 \lbrack_{\mathbb{A}_{\R}} ) \overset{?}{=} \frac{ \s }{ 2 ω } $. Dies führt nach meinem Verständnis dazu, dass die superial kleinen Summanden vollständig verschwinden und alle Koordinaten rein reell algebraische werden.
(In Arbeit …)
$ 2 \cdot \# ( [ -1, 1 ]_{\mathbb{A}_{\R}} ) - 2 = 2 \cdot \left( 2 \cdot \frac{ \s }{ 2 ω } \right) - 2 = \frac{ 2 \s }{ ω } - 2 $
(In Arbeit …)
Die Betrachtung der Verhältnisse im Kreis verlagert die Fragestellung der sinnvollen Koeffizienten geometrisch ins Endliche
(In Arbeit …)
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \left( \forall a^{+} \in \mathbb{A}_{\R}^{+} \right) \left[\; a^{+} \cdot \s\;\;\;\overset{?}{\in}\;\;\;\mathbb{N}_{\infty} \;\right] } \] | (SN.SinK.7) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\left( \forall a^{+} \in \mathbb{A}_{\R}^{+} \right) \left[\; a^{+} \cdot \s\;\;\;\overset{?}{\in}\;\;\;\mathbb{S}_{\N} \;\right] } \] | (SN.SinK.8) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\left( \forall a^{+} \in \mathbb{A}_{\R}^{+} \right) \left[\; \left( e^{a^{+} \cdot \i \cdot 2 π} \right)^{\s}\;\;\;\overset{?}{=}\;\;\;1 \;\right] } \] | (SN.ArGeo.O.21) |
(In Arbeit …)
Gibt es überrationale Zahlen, die sich nicht wie die ganzen Wurzeln aus natürlichen Zahlen verhalten?
Wir wollen schauen, welche reell algebraischen Zahlen der Menge $ \mathbb{A}_{\R} $ es noch geben kann, die durch ein Produkt mit einem unendlichen Teilprodukt des Primzahl-Flächenprodukts
von $ \s $ noch aktual unendliche natürliche Zahlen ergeben können.
Hier ein mögliches Beispiel, dass sich an überrationale Zahlen, genauer an überrationalen Brüchen, orientiert.
Denn es gibt ja auch noch die Möglichkeit, dass zum Beispiel nicht alle endlichen aktual unendlichen Potenzen der Zwei schon ausreichen, wie bei irrationalen Wurzeln
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \sqrt{2}\;\;\;=\;\;\;2^{\frac{ 1 }{ 2 }}\;\;\;=\;\;\;\frac{ 2^{\frac{ 1 }{ 2 }} \cdot 2^{ω} }{ 2^{ω} }\;\;\;=\;\;\;\frac{ 2^{ω + \frac{ 1 }{ 2 }} }{ 2^{ω} } \;\; , } \] | (SN.ÜV.28) |
sondern nur eine der unendlichen Potenzen der Zwei dies leistet, alle anderen aber nicht:
(In Arbeit …)
| → |
|
| |
Resonanz in der Arithmetik der Geometrie |
|
Eine grundlegendes Prinzip der Existenz: die Resonanz
| ← |
|
Unsere superiale Basis $ \s $ geht über ihre Primfaktorzerlegung in „Resonanz“ mit jeder ganzen, jeder rationalen und sogar jeder algebraischen Zahl, also auch mit allen Brüchen, ganzen Exponenten und ganzen Wurzeln sowie deren algebraische Kombinationen.
Wie wird Resonanz in diesem Zusammenhang verstanden?
Resonanz bedeutet hier, dass alle endlichen algebraischen Zahlen sowohl auf der Grundlage der superial kleinen Basis $ \s^{-1} $ „tanzen“ – also „schwingen“ –, als auch der Ganzheit $ \s $ entgegenstreben, die sie als größere Vollkommenheit quasi anzieht.
Ich lasse mich hier von dynamischen Ausdrücken inspirieren, obwohl es zunächst scheint, als wenn wir es hier mit rein statischen Verhältnissen zu tun haben. Denn mir ist bewusst, dass die Primzahlen zwar statisch erscheinen, gleichzeitig aber aus dem dynamischen Prozess des Zählens resultieren, ohne den sie für mich nicht wirklich denkbar erscheinen.
Zum einen erscheint jede reell algebraische Zahl $ a \in \mathbb{A}_{\R} $ aus der Perspektive ihres grundlegenden Rasters der Größenordnung $ \s^{-1} $ als ganze Zahl. Mit anderen Worten: $ z \cdot \s^{-1} = a $ bedeutet, dass ihr Faktor $ z = a \cdot \s $ eine ganze Zahl ist, wenn auch eine aktual unendlich große.
Zum anderen fallen die kleinsten ganzzahligen „Schwingungsknoten“ – also die Primzahl-Konstruktoren ($ p $-adischen Bewertungen) von $ a $ – mit dem grundlegenden Raster zusammen.
Damit liegt zum Beispiel auch $ 2^{\frac{ 1 }{ 2 }} \cdot 2^{ω} $ auf dem im Unendlichen ganzzahligen Raster $ 2^{q} \cdot 2^{ω} $, wenn $ q \in \mathbb{Q} $. Wollen wir dieses auf alle ganzzahligen Wurzeln und schließlich auf alle reell algebraischen Zahlen ausweiten, dann brauchen wir allerdings das größere Raster von $ \s $. Wodurch wir dann $ 2^{\frac{ 1 }{ 2 }} \s $ als ganze Zahl erhalten. Wenn wir dieses Rastern dann aber auf endliche Zahlen verkleinert haben wollen, so skalieren wir es mit dem Faktor $ \s^{-1} $ herunter auf $ \left( 2^{\frac{ 1 }{ 2 }} \s \right) \s^{-1} $ und erhalten dann $ 2^{\frac{ 1 }{ 2 }} $, also unsere endliche Wurzel, die auf dem aktual unendlich kleinen Raster der Weite $ \s^{-1} $ liegt.
Dieses enthält allerdings unendlich kleine ganze Summanden $ a + z \cdot \s^{-1} $, mit $ a \in \mathbb{A}_{\R} $ und $ z \in \mathbb{Z} $. Wollen wir diese nicht haben, dann nehmen wir im Endlichen einfach nur die reell algebraischen Koeffizienten $ a $, die auch alle auf diesem Raster liegen, wenn $ z = 0 $.
Verfeinerung der Perspektive der Resonanz
… führt vermutlich zur Riemannschen Vermutung
Führen wir diese Perspektive der Resonanz weiter aus, indem wir sie auf den Prozess des Zählens beziehen, dann könnte uns dies zur Riemannschen Vermutung führen.
(In Arbeit …)
| → |
| |
Fußnoten |
|
| 1. | Vgl. Haramein, Die Entschlüsselung des Universums, Ⅰ Unendlich und doch begrenzt, S. 11-17, hier S. 12-13. | |
| 2. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Ordinalzahl. | |
| 3. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Vollständige Induktion, Das Axiom der vollständigen Induktion. Vgl. Wikipedia, Unendlichkeitsaxiom, Formulierung; Bedeutung für die Mathematik, Natürliche Zahlen. | |
| 4. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Algebraische Zahl. | |
| 5. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Kontinuumshypothese. | |
| 6. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Mächtigkeit. | |
| 7. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Kreisteilungspolynom. |
| |
Stand 20. November 2025, 23:00 CET.
-
Permanente Links:
(Klicke auf die Archivlogos
zum Abruf und Ansehen
der Archive dieser Seite.) -

-
archive.todaywebpage capture