←	Superial-Zahlen

Einleitung

Die Zahlentheorie der Analysis

Mit den Superial-Zahlen die fraktale Struktur des Aktual-Unendlichen entdecken

Wie wir sehen werden erhalten wir mit den hier entwickelten Superial-Zahlen etwas ganz besonderes: Formal gesprochen sind sie eine abelsche Gruppe und bezüglich der Addition und Multiplikation ein aktual unendlicher angeordneter algebraischer Körper,. Mit ihnen erweitern wir die rationalen Zahlen und durch den Beweis der Überrationalitätsvermutung, sowie durch auf ihm aufbauende Beweise, sogar die Menge der Radikale der algebraischen Zahlen, inklusive aller Ausdrücke der irrationalen Wurzeln, die durch die Grundrechenarten entstehen, auf fraktale Weise ins Aktual-Unendliche. So geben wir der aktualen Unendlichkeit eine facettenreiche und der Geometrie eine fundamentale arithmetische und fraktale Struktur.

Mit den Superial-Zahlen kommen wir in die Lage aktual unendlich kleine Differenzen zu bilden, mit denen wir, bis ins aktual unendlich kleine, präzise Ableitungen beschreiben und berechnen können, ohne den Limes zu benutzen.

Auch können wir Integrale mit wohldefinierten aktual unendlich kleinen Zählschritten beschreiben, deren Anzahl dann aktual unendlich groß sind und sich so wieder zu endliche Zahlen aufsummieren.

Nutzen wir auch die Theorie der Biordinalzahlen so können wir Summen ausrechnen, die nach meinem Wissen bisher nicht durch aktual unendliche Zahlen ausgedrückt werden konnten: Die Summe aller endlichen ganzen Zahlen oder die Summe der Realanteile aller algebraischen Zahlen beispielsweise.

Über die Struktur, die dabei sichtbar wird, eröffnet sich in meinen Augen ein ganz neuer Kosmos der Zahlentheorie. Denn wir können die endlichen Primzahlen mit unserer dadurch entdeckten, neuen aktual unendlichen Basis $ \s $ in Zusammenhang bringen, indem wir diese durch Primzahlen definieren, wie wir noch sehen werden.

Wir erhalten zum Beispiel auch natürliche Superial-Zahlen, ganze Superial-Zahlen und superiale Primzahlen; aktual unendlich kleine Einsen und aktual unendlich große Einsen. Auch können die ganzen Superial-Zahlen gerade oder ungerade sein und so weiter und so fort. Erstaunlich viele der uns bekannten wichtigen Eigenschaften der endlichen Zahlen erweitern sich ins aktual unendlich Kleine und Große.

Und nicht zuletzt sind die Superial-Zahlen ein Stellenwertsystem zur Basis $ \s $, wo die Ziffern alle positiven wie auch negativen Realanteile der algebraischen Zahlen sein können.

Wir erschaffen so eine Zahlentheorie der Analysis, die auf Primzahlen basiert, die im unendlich großen Produkt aller endlichen Primzahlen zur $ ω $-ten Potenz ihre Grundlage findet, der superialen Basis $ \s $. Dabei finden wir heraus, dass $ ω $ selbst – die vollständige Induktion – ein Primzahlprodukt ist.

Die superiale Basis $ \s $ ist nicht einfach irgendeine aktual unendliche Zahl. Sie ist so auf die einfachste Weise symmetrisch strukturiert, dass sie genau zu den Eigenschaften der rationalen und algebraischen Zahlen passt, sodass diese als ihre Koeffizienten, mit ihr im Produkt, immer aktual unendlich große ganze Zahlen ergeben. Daher spielt die superiale Basis $ \s $ eine zwar andere, aber vergleichbare Rolle für das Aktual-Unendliche, wie die imaginäre Einheit $ \i $ für die komplexen Zahlen. Ich habe mir Ableitungen und Integrale genau angeguckt und versucht zu verstehen, welche Eigenschaften $ \s $ hat. Darüber hab ich letztendlich die Definition von $ \s $ als aktual unendliches Primzahlprodukt in Kombination mit vollständiger Induktion gefunden.

Wie sagen wir im Englischen so schön: »Lets go for it!«

Motivation

In der Schule fand ich Ableitungen und Integrale immer sehr faszinierend. Es war für mich erstaunlich, wie man über die Unendlichkeit ganz neue Erkenntnisse und Formeln gewinnen konnte. Daraus hat sich damals ein tiefes Bedürfnis entwickelt zu verstehen, was dabei genau vor sich geht. Ich spielte viel mit dem Ansatz der Ableitung herum, was schließlich dazu führte, dass ich begriff, dass der dort verwendete Limes nicht nur dazu führt, dass ein bestimmtes Glied der sich ergebenen Summe dominant in den Vordergrund tritt und das Ergebnis bestimmt. Mir wurde auch klar, dass all die anderen Summanden, die unendlich klein und damit scheinbar unbedeutend wurden, eine Welt darstellten, die so quasi im Nirvana versank.

Genau diese „versunkene“ Welt weckte mein Interesse. Irgendwie war ja auch klar, dass beim Integrieren die versunkene Welt schließlich wieder auftauchen musste. Wie könnte sie da unwiederbringlich „vernichtet“ worden sein? Durch das Herumspielen begriff ich: Wir können auch ins Unendliche gehen, ohne den Limes zu benutzen! Ohne, dass man die versinkenden Summanden wirklich zu Null werden lässt, indem man sie als Null definiert.

Formale Einschränkung

Um nachfolgend genau zu arbeiten, möchte ich an dieser Stelle vorab deutlich machen, dass im folgenden die Funktionsparameter – meistens $ x $ – die sinnvollen Koeffizienten der Superial-Zahlen der Menge $ \mathbb{A}_{\S} $ sind. Nach jetzigem Stand sind dies mindestens alle realen Koeffizienten der algebraischen Zahlen, die durch Radikale darstellbar sind. Dass genau alle reell algebraischen Zahlen in der Menge $ \mathbb{A}_{\S} $ sind vermuten wir, ist jedoch noch zu beweisen.

Transzendente Zahlen scheinen hingegen als Koeffizienten nicht sinnvoll.

Ableitung genau verstehen

Das Nicht-Verschwinden aller Summanden funktioniert dann, wenn wir die beim Ableiten gegen Null gehenden Summanden selber als unendlich klein, aber nicht als verschwindend betrachten. Wir setzten den gegen Null gehenden Summanden zu $ \Delta x ≔ \s^{-1} $, zum Kehrwert der superialen Basis $ \s $, die wir im Verlauf genauer ergründen werden:

\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { f'(x)\;\;\;=\;\;\;\lim\limits_{\Delta x \rightarrow +0}{ \frac{ f(x + \Delta x) - f(x) }{ \Delta x } } } \]	(SN.AbIn.1)
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \lim\limits_{\Delta x \rightarrow +0}{ \Delta x }\;\;\;\widehat{=}\;\;\;\s^{-1} } \]	(SN.AbIn.2)
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { f'(x)\;\;\;≔\;\;\;\frac{ f(x + \s^{-1}) - f(x) }{ \s^{-1} } } \]	(SN.AbIn.3)

Dies vertiefen wir auf der Seite Ableitungen und Integrale.

Dabei ist $ \s^{-1} $ ein neues Symbol, über das ich zunächst nur annahm, dass es kleiner als jede positive Zahl war und doch größer als Null. Ähnlich wie bei den komplexen Zahlen die imaginäre Einheit $ \i $ war auch $ \s^{-1} $ eine neue Einheit, die ich als superial kleine Einheit bezeichne. In der Mathematik ist es kein Problem ein neues Symbol zu kreieren und zu definieren, solange sich dadurch keine Widersprüche ergeben.

Die superial kleine Einheit $ \s^{-1} $ führte dazu, dass die sonst bei der Ableitung verschwindenden Summanden $ a_{k} $ nicht verloren gehen, sondern in unendlich kleinen Dimensionen $ a_{-1} \s^{-1} + a_{-2} \s^{-2} + a_{-3} \s^{-3} + \cdots $ erhalten blieben, also in einer superial kleinen Welt. Von hier können sie auch beim Integrieren wieder auftauchen. Die Dimension $ a_{0} \s^{0} = a_{0} $ stellt dann die uns bekannten, endlichen Zahlen dar, weil $ \s^{0} = 1 $ ist, wie gewohnt.

Konkrete Ableitungen
Nun zwei Beispiele, um anschaulich zu verstehen, was vor sich geht:

So ergibt sich als Beispiel für die Funktion $ f(x) = x^{2} $:

\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}f'(x)\;\;\;=\;\;\;\frac{ \left( x + \s^{-1} \right)^{2} - x^{2} }{ \s^{-1} } } \]	(SN.AbIn.10)
► einblenden
▼ ausblenden
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}f'(x)\;\;\;=\;\;\;\frac{ \left( x^{2} + 2 x \cdot \s^{-1} + \s^{-2} \right) - x^{2} }{ \s^{-1} } } \]	(SN.AbIn.11)
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}f'(x)\;\;\;=\;\;\;\frac{ 2 x \cdot \s^{-1} + \s^{-2} }{ \s^{-1} } } \]	(SN.AbIn.12)
▲ ausblenden
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}f'(x)\;\;\;=\;\;\;2 x + \s^{-1} } \]	(SN.AbIn.13)

Wenn wir also $ \s^{-1} $ zu Null setzen, dann kommt das übliche Ergebnis $ f'(x) = 2 x $ heraus.

Für $ f(x) = x^{3} $ ergibt sich dann:

\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}f'(x)\;\;\;=\;\;\;\frac{ \left( x + \s^{-1} \right)^{3} - x^{3} }{ \s^{-1} } } \]	(SN.AbIn.14)
► einblenden
▼ ausblenden
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}f'(x)\;\;\;=\;\;\;\frac{ \left( x^{3} + 3 x^{2} \cdot \s^{-1} + 3 x \cdot \s^{-2} + s^{-3} \right) - x^{3} }{ \s^{-1} } } \]	(SN.AbIn.15)
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}f'(x)\;\;\;=\;\;\;\frac{ 3 x^{2} \cdot \s^{-1} + 3 x \cdot \s^{-2} + \s^{-3} }{ \s^{-1} } } \]	(SN.AbIn.16)
▲ ausblenden
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}f'(x)\;\;\;=\;\;\;3 x^{2} + 3 x \cdot \s^{-1} + \s^{-2} } \]	(SN.AbIn.17)

Wenn wir also $ \s^{-1} $ zu Null setzen, dann kommt das übliche Ergebnis $ f'(x) = 3 x^{2} $ heraus.

So können wir sehr genau verfolgen, was vor sich geht, und nichts verschwindet.

Integration genau verstehen

Beim Integral müssen wir nun den Prozess des Differenzierens wieder Rückgängig machen und lernen viel Interessantes dabei, wenn wir herausfinden, wie das geht.

Ganze Superial-Zahlen
Interessanter wird es noch, wenn wir uns nun mit der Umkehrung der Ableitung aus der neuen Perspektive beschäftigen, mit der Integration:

Beim Flächenintegral, von dem wir hier sprechen, handelt es sich um eine Summe aus unendlich schmalen und endlich hohen Flächen. In ihm werden all die unendlich kleinen Differenzen aufsummiert, aus der sich die Ableitung ergibt und die gemeinsam zurück zum Verlauf der Ausgangsfunktion führen.

Wie groß die Schritte der Summation sind, erkennen wir an der Ableitung. Die aufsummierten Flächen gleichen den Ergebnis-Differenzen der Ableitung $ f'(x) $ in unendlich kleinen Einheiten und haben damit deren Höhe. Ihre Streifenbreite ist $ \Delta x = \s^{-1} $, wie die Funktionsparameter-Differenz der Ableitung. Dabei ist $ \s^{-1} $ eine unendlich kleine Einheit. Eine aktual unendlich kleine Eins $ 1 \s^{-1} $.

Auf der anderen Seite müssen wir eine unendlich große und ganze Anzahl der Streifen summieren. Es müssen genau $ \s $ Streifen sein, damit sich die $ \s^{-1} $ breiten Streifen zu einer endlich großen Zahl aufsummieren und wir das Integral erhalten. Damit ist klar, dass $ \s $ eine unendlich große, ganze und positive Zahl ist, eine aktual unendlich große Eins $ 1 \s $. Es muss also formal möglich sein, alle positiven ganzen Zahlen von den endlichen bis $ \s $ zu zählen, um die Summe für das Integral zu beschreiben:

Sei $ \mathbb{S}_{\Z} $ die Menge der ganzen Superial-Zahlen, eine Teilmenge der Superial-Zahlen $ \mathbb{S} $. Seien $ \lbrack a, b \lbrack_\mathbb{\mathbb{S}_{\Z}} $ die ganzen Superial-Zahlen in der Intervall-Menge von $ a $ bis $ b $, ohne $ b $, aus $ \mathbb{S}_{\Z} $:

\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { [0, x \cdot \s[_{\mathbb{S}_{\Z}}\;\;\;\subset\;\;\;\mathbb{S}_{\Z} } \]

(SN.Ein.1)

Die ganzen Superial-Zahlen können grundsätzlich Summanden aller natürlichen Potenzen von $ \s $, also Null und größer, enthalten; in der nullten Potenz, im endlichen Summanden, eben nur endliche ganze Zahlen; in den höheren Potenzen dann alle Realanteile algebraischer Zahlen als Koeffizienten, also auch irrationale Zahlen, wie Wurzeln.

Prinzipiell haben ganze Superial-Zahlen mit der maximalen Potenz Eins – $ \s^{1} = \s $ –, die wir in unseren Beispielen zum Integrieren als Grundlage benötigen, also die Form:

\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \left( \forall a \in \mathbb{A}_{\S} \right) \left( \forall z \in \mathbb{Z} \right) \left[\; a \cdot \s + z\;\;\;\in\;\;\;\mathbb{S}_{\Z} \;\right] } \]

(SN.Ein.2)

Für die genaue Menge können wir, angelehnt an die später gefundene Formel SN.Eig.SVS.1, folgende Beschreibung geben – wie immer mit $ x \in \mathbb{A}_{\S} $:

► einblenden
▼ ausblenden
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { [ 0, \s [_{\mathbb{S}_{\Z}}\;\;\;=\;\;\;\\ \quad \left\{\; r\;~\middle|~\;\left( \forall a \in [ 0, 1 ]_{\mathbb{A}_{\S}} \right) \left( \forall n \in \mathbb{N} \right) \left( \forall z \in \mathbb{Z} \right) \left( \forall z^{-} \in \mathbb{Z}^{-} \right) \\ \qquad\qquad\quad \left[\; r\;\;\;=\;\;\;\begin{cases} n & \text{ falls } a = 0 \\ a \cdot \s + z & \text{ falls } 0 < a < 1 \\ \s + z^{-} & \text{ falls } a = 1 \end{cases} \;\right] \;\right\} } \]	(SN.Eig.SVS.1)
▲ ausblenden
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { [ 0, x \cdot \s [_{\mathbb{S}_{\Z}}\;\;\;=\;\;\;\\ \quad \left\{\; r\;~\middle|~\;\left( \forall a \in [ 0, 1 ]_{\mathbb{A}_{\S}} \right) \left( \forall n \in \mathbb{N} \right) \left( \forall z \in \mathbb{Z} \right) \left( \forall z^{-} \in \mathbb{Z}^{-} \right) \\ \qquad\qquad\quad \left[\; r\;\;\;=\;\;\;\begin{cases} n & \text{ falls } a = 0 \\ a \cdot \s + z & \text{ falls } 0 < a < x \\ x \cdot \s + z^{-} & \text{ falls } a = x \end{cases} \;\right] \;\right\} } \]	(SN.AbIn.IN.2)

Es handelt sich also konkret um folgende ganze Superial-Zahlen, die auszugsweise so aussehen, wobei Beginn und Ende exakt stimmen:

\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { [0, x \cdot \s [_{\mathbb{S}_{\Z}}\;\;\;=\;\;\;\\ \quad \left\{\; \quad\, 0, 1, 2, \cdots n, \cdots \\ \quad\quad\; \quad \vdots \\ \quad \quad \cdots \frac{1}{2} x \s + z^{-}, \cdots \frac{1}{2} x \s - 1,\; \frac{1}{2} x \s,\; \frac{1}{2} x \s + 1, \cdots \frac{1}{2} x \s + n, \cdots \\ \quad\quad\; \quad \vdots \\ \quad \quad \cdots \frac{2}{3} x \s + z^{-}, \cdots \frac{2}{3} x \s - 1,\; \frac{2}{3} x \s,\; \frac{2}{3} x \s + 1, \cdots \frac{2}{3} x \s + n, \cdots \\ \quad\quad\; \quad \vdots \\ \quad \quad \cdots \, x \s + z^{-}, \cdots x \s - 2, x \s - 1 \quad \right\} } \]

(SN.AbIn.IN.3)

Jetzt haben wir zwar die richtige Anzahl an Schritten, aber sie sind nicht fein genug, sollen sie doch eigentlich von Null bis $ x $ in $ \s^{-1} $ kleinen Schritten laufen. So müssen wir die Zahlen dieses Intervals der ganzen Superial-Zahlen also mit $ \s^{-1} $ multiplizieren und auf diese Weise auf eine superial kleine Größenordnung skalieren.

Alternativ können wir auch eine Menge definieren, in der alle Zahlen schon mit $ \s^{-1} $ multipliziert sind, wie in ›Skalierung der superialen Ebene einer Teilmenge der Superial-Zahlen‹ definiert:

\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \mathbb{S}^{y}_{\Z}\;\;\;≔\;\;\;\left\{\; a\;~\middle|~\;\left( \forall z \in \mathbb{S}_{\Z} \right) \left[ a = z \cdot \s^{y} \right] \;\right\} } \]	(SN.Form.F.24)
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}\mathbb{S}^{-1}_{\Z}\;\;\;=\;\;\;\left\{\; a\;~\middle|~\;\left( \forall z \in \mathbb{S}_{\Z} \right) \left[ a = z \cdot \s^{-1} \right] \;\right\} } \]	(SN.Ein.3)

Im benötigten Mengen-Intervall laufen die Zahlen in $ x \cdot \s $ unendlich kleinen Schritten der Größe $ \s^{-1} $ durch. Auszugweise sieht diese Intervall-Menge von unendlich feinschrittigen superial kleinen ganzen Superial-Zahlen folgendermaßen aus, wobei Beginn und Ende exakt stimmen und sich ihre Größensortierung nach der lexikografischen Ordnung, unter Berücksichtigung der Potenz von $ \s $, richtet:

\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { [0, x[_{\mathbb{S}^{-1}_{\Z}}\;\;\;=\;\;\;\\ \quad \left\{\; \quad\, 0 \s^{-1}, 1 \s^{-1}, 2 \s^{-1}, \cdots \\ \quad\quad\; \quad \vdots \\ \quad \quad \cdots \frac{1}{2} x - 2 \s^{-1},\; \frac{1}{2} x - \s^{-1},\; \frac{1}{2} x,\; \frac{1}{2} x + \s^{-1},\; \frac{1}{2} x + 2 \s^{-1}, \cdots \\ \quad\quad\; \quad \vdots \\ \quad \quad \cdots \frac{2}{3} x - 2 \s^{-1},\; \frac{2}{3} x - \s^{-1},\; \frac{2}{3} x,\; \frac{2}{3} x + \s^{-1},\; \frac{2}{3} x + 2 \s^{-1}, \cdots \\ \quad\quad\; \quad \vdots \\ \quad \quad \cdots \, x - 3 \s^{-1}, x - 2 \s^{-1}, x - \s^{-1} \quad \right\} } \]

(SN.AbIn.IN.1)

Nun können wir das allgemeine Integral recht einfach definieren:

\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \int_{a}^{x} f'(n) \,dn\;\;\;\widehat{=}\;\;\;\!\!\! \sum_{ \forall n \in [a, x[_{\mathbb{S}^{-1}_{\Z}} } \!\!\! f'(n) \cdot \s^{-1} } \]	(SN.AbIn.IN.12)
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { f(x)\;\;\;≔\;\;\;f(a) + \!\!\! \sum_{ \forall n \in [a, x[_{\mathbb{S}^{-1}_{\Z}} } \!\!\! f'(n) \cdot \s^{-1} } \]	(SN.AbIn.IN.15)

Diese Summe ist so definiert, dass sie im Falle von $ x < 0 $ negativ wird.

So bekommen wir einen neuen Ausdruck für das Integral in Form einer originären Summe.

Wir versenken die Funktionswerte der Ableitung also im unendlich Kleinen, als unendlich dünne Streifen, und lassen die ursprüngliche Funktion aus der Versenkung wieder im Endlichen erscheinen, durch endlos feines Aufsummieren.

Hierzu benötigen wir ganze Superial-Zahlen, skaliert ins superial kleine. Diese werden wir im folgenden Beispiel besser praktisch kennenlernen.

Konkretes Integral
Nun ein Beispiel, um anschaulich zu verstehen, was vor sich geht. Dieses finden wir in der Stellenwertsystem-Schreibweise auch im Abschnitt ›Beispiel eines konkreten Integrals‹.

Wir nehmen das erste obige $ f(x) = x^2 $ mit dem Ableitungsergebnis $ f'(x) = 2 x + \s^{-1} $ und setzen dies in unsere Integralformel ein:

\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { f(x)\;\;\;=\;\;\;f(0) \; + \!\!\! \sum_{ \forall n \in [0, x[_{\mathbb{S}^{-1}_{\Z}} } \!\! \left( 2 n + \s^{-1} \right) \cdot \s^{-1} } \]	(SN.Ein.4)
► einblenden
▼ ausblenden
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}f(x)\;\;\;=\;\;\;f(0) + \!\!\! \sum_{ \forall n \in [0, x[_{\mathbb{S}^{-1}_{\Z}} } \!\! \left( 2 n \cdot \s^{-1} + \s^{-2} \right) } \]	(SN.Ein.5)
▲ ausblenden
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}f(x)\;\;\;=\;\;\;f(0) \; + \; 2 \cdot \s^{-1} \cdot \!\!\!\! \sum_{ \forall n \in [0, x[_{\mathbb{S}^{-1}_{\Z}} } \!\!\!\! n \; + \; \s^{-2} \cdot \!\!\!\! \sum_{ \forall n \in [0, x[_{\mathbb{S}^{-1}_{\Z}} } \!\!\!\! 1 } \]	(SN.Ein.6)

Anschließend haben wir die innere und äußere Summe in zwei getrennte Summen umgeformt.

Die hintere Summe addiert die Eins $ x \cdot \s $ mal, weil die Schrittgröße hierbei ja keine Rolle spielt, sondern nur die Schrittanzahl, und das ergibt natürlich auch $ x \cdot \s $:

► einblenden
▼ ausblenden
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}f(x)\;\;\;=\;\;\;f(0) \; + \; 2 \cdot \s^{-1} \cdot \!\!\!\! \sum_{ \forall n \in [0, x[_{\mathbb{S}^{-1}_{\Z}} } \!\!\!\! n \; + \; \s^{-2} \cdot x \cdot \s } \]	(SN.Ein.7)
▲ ausblenden
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}f(x)\;\;\;=\;\;\;f(0) \; + \; 2 \cdot \s^{-1} \cdot \!\!\!\! \sum_{ \forall n \in [0, x[_{\mathbb{S}^{-1}_{\Z}} } \!\!\!\! n \; + \; x \cdot \s^{-1} } \]	(SN.AbIn.IN.20)

Die übrige Summe der superial kleinen ganzen Zahlen der ersten $ x \cdot \s $ Elemente dieser Menge, mit der Null, ergibt sich aus der angepassten Gaußschen Summenformel, wie bei den Biordinalzahlen im Abschnitt ›Die Summe aller natürlichen Zahlen bis ins Aktual-Unendliche berechnen‹ nach Formel BO.Ein.NE.82 angegeben, weil die Menge $ \mathbb{S}_{\N} $ nach Formel SN.Eig.SVS.43 zur Klasse $ \mathbb{K}_{\infty,g} $ der Gauß-Summen äquivalenten Klassen – so auch Mengen – gehört:

\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \mathbb{S}_{\N}\;\;\;\in\;\;\;\mathbb{K}_{\infty,g} } \]	(SN.Eig.SVS.43)
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \left( \mathbb{M} \in \mathbb{K}_{\infty,g} \right) \left( \forall n \in \mathbb{M} \right) \left[\; \sum_{ \forall i \in [ 0, n [_{\mathbb{M}} } \!\!\!\! i\;\;\;=\;\;\;\frac{ n^{2} - n }{ 2 } \;\right] } \]	(BO.Ein.NE.82)
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}\left( \forall n \in \mathbb{S}_{\N} \right) \left[\; \sum_{ \forall i \in [ 0, n [_{\mathbb{S}_{\N}} } \!\!\!\! i\;\;\;=\;\;\;\frac{ n^{2} - n }{ 2 } \;\right] } \]	(SN.Ein.8)

Diese Summe ist extra darauf angepasst, dass sie auch für aktual unendlich große Werte von $ n $, also für aktual unendlich große natürliche Zahlen, gilt.

Wir müssen nur berücksichtigen, dass die Werte der gesuchten Summe in superial kleinen Schritten daher kommen: Das bedeutet, dass wir es mit $ x \cdot \s $ Elementen zu tun haben – anstatt mit $ x $ –, was in der oben stehenden Formel auf der Ergebnisseite als $ x \cdot \s $ für $ n $ eingeht. Jedoch ist die Größe der einzelnen Summanden auf Ebene der ganzen Zahlen superial klein, sodass wir das Ergebnis um eine superiale Potenz $ \s $ verringern müssen:

\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}\sum_{ \forall n \in [0, x[_{\mathbb{S}^{-1}_{\Z}} } \!\!\!\! n\;\;\;=\;\;\;\frac{ \left( x \cdot \s \right)^{2} - x \cdot \s }{ 2 } \cdot \s^{-1} } \]	(SN.Ein.9)
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\sum_{ \forall n \in [0, x[_{\mathbb{S}^{-1}_{\Z}} } \!\!\!\! n\;\;\;=\;\;\;\frac{ x^{2} \cdot \s - x }{ 2 } } \]	(SN.AbIn.IN.23)

Diese Summe haben wir auch noch einmal im Einzelnen im Rahmen der Superial-Zahlen aus ihren Teilsummen im Abschnitt ›Direkte Herleitung der angepassten Gaußschen Summenformel‹ hergeleitet, um zu zeigen, und damit ganz sicher zu gehen, dass diese richtig ist.

Das ist genau das gesuchte Ergebnis, was wir sofort durch Überprüfung sehen. Dies eingesetzt in Formel SN.AbIn.IN.20 ergibt

\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}f(x)\;\;\;=\;\;\;f(0) \; + \; 2 \cdot \s^{-1} \cdot \frac{ x^{2} \cdot \s - x }{ 2 } \; + \; x \cdot \s^{-1} } \]	(SN.Ein.10)
► einblenden
▼ ausblenden
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}f(x)\;\;\;=\;\;\;f(0) \; + \; x^{2} - x \cdot \s^{-1} \; + \; x \cdot \s^{-1} } \]	(SN.Ein.11)
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}f(x)\;\;\;=\;\;\;f(0) \; + \; x^{2} } \]	(SN.Ein.12)
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}f(x)\;\;\;=\;\;\;0^{2} \; + \; x^{2} } \]	(SN.Ein.13)
▲ ausblenden
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}f(x)\;\;\;=\;\;\;x^{2} } \]	(SN.Ein.14)

und ist auch das erwartete Ergebnis.

Wie wir sehen, ist es tatsächlich mit den Superial-Zahlen möglich, ein Integral eines Polynoms explizit auszurechnen. Dies geht so einfach schon mal mit jedem Integral eines Polynoms, ist bei Polynomen höheren Grades aber natürlich entsprechend aufwendiger. Offensichtlich ist dabei, dass wir so recht einfach verstehen, was bei der Berechnung des Integrals im Detail vor sich geht.

Und das ist ja eines meiner Ziele, beim Ableiten und besonders beim Integrieren nicht so eine Black-Box vor uns zu haben.

Auf diese Weise ergibt sich für uns ein zunehmend konkretes Bild davon, was die superiale Basis $ \s $ eigentlich ist und was wir mit $ \s $ alles anfangen können. Aus diesem besser werdendem Bild, und besonders über die nähere Beleuchtung der Frage der ganzen Superial-Zahlen, kommen wir gleich zu einer ganz bemerkenswerten Definition unserer superialen Basis $ \s $.

Kleiner Ausblick zwischendurch

Wir werden im Folgenden noch sehen, dass dieses Vorgehen weitere neue Erkenntnishorizonte eröffnet.

Nur zum Appetit machen können wir hier schon mal kurz zeigen, dass die zuletzt errechnete Summe SN.AbIn.IN.23 sich auch folgendermaßen beschreiben lässt, wenn wir ihren Bruch in zwei Teile zerlegen:

\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \sum_{ \forall n \in [0, x[_{\mathbb{S}^{-1}_{\Z}} } \!\!\!\! n\;\;\;=\;\;\;\frac{ x^{2} \cdot \s }{ 2 } - \frac{ x }{ 2 } } \]

(SN.AbIn.NU.1)

Der erste Summand kann später im Abschnitt ›Summen zur Integration von $ \langle 2 x\rangle .\!\langle 1\rangle $‹ aus der Struktur der ganzen Superial-Zahlen und unseren Erkenntnissen in der Theorie der Biordinalzahlen berechnet werden zu:

\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \frac{ x^{2} \cdot \s }{ 2 }\;\;\;=\;\;\;\left( \sum_{ \forall a \in [ 0, x [_{\mathbb{A}_{\S}}} \!\! a \;\; + \! \sum_{ \forall a \in ] 0, x ]_{\mathbb{A}_{\S}}} \!\! a \right) \cdot ω } \]	(SN.AbIn.NU.32)
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\frac{ x^{2} \cdot \s }{ 2 }\;\;\;=\;\;\;\# [ 0, x [_{\mathbb{A}_{\S}} \; \cdot \; x \cdot ω } \]	(SN.AbIn.NU.25)

Dabei steht das Symbol $ ω $ für die Anzahl der endlichen natürlichen Zahlen, mit der Null, in der Menge $ \mathbb{N} $; also für die vollständige Induktion. Und das Symbol $ \# $ gibt die Anzahl der Elemente der nachfolgenden Menge an.

Gleiches gilt auch für den zweiten Summanden:

\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { - \frac{ x }{ 2 }\;\;\;=\;\;\;\# [ 0, x \, [_{\mathbb{A}_{\S}} \; \cdot \sum_{ \forall z \in \mathbb{Q} } z \cdot s^{-1} } \]	(SN.AbIn.NU.8)
► einblenden
▼ ausblenden
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}- \frac{ x }{ 2 }\;\;\;=\;\;\;\# [ 0, x \, [_{\mathbb{A}_{\S}} \, \cdot \; \frac{ -ω }{ \s } } \]	(SN.AbIn.NU.9)
▲ ausblenden
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}- \frac{ x }{ 2 }\;\;\;=\;\;\;- \; \# [ 0, x \, [_{\mathbb{A}_{\S}} \, \cdot \; \frac{ ω }{ \s } } \]	(SN.AbIn.NU.10)

Hierbei ist es vermutlich für den ein oder anderen erstaunlich, dass ganz unabhängig von den hier entwickelten Superial-Zahlen in der Theorie der Biordinalzahlen deutlich wird, dass genauso viele endliche rein negative ganze Zahlen existieren, wie es endliche natürliche Zahlen gibt, also endliche positive ganze Zahlen, mit der Null. Demnach finden wir, bei genauer Untersuchung, eine fundamentale Asymmetrie zwischen der ontologischen Struktur der endlichen ganzen Zahlen und der Verteilung ihrer Werte (siehe Abbildung 1, im Abschnitt ›Die Struktur von s‹). Dadurch ergibt die Summe aller endlichen ganzen Zahlen die aktual unendlich große negative Zahl $ -ω $ (siehe Formel BO.Ein.NE.12).

Addieren wir nun beide Summanden, so erhalten wir:

\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}\sum_{ \forall n \in [0, x[_{\mathbb{S}^{-1}_{Z}} } \!\!\!\! n\;\;\;=\;\;\;\# [ 0, x [_{\mathbb{A}_{\S}} \; \cdot \; x \cdot ω \; - \; \# [ 0, x \, [_{\mathbb{A}_{\S}} \, \cdot \; \frac{ ω }{ \s } } \]	(SN.AbIn.NU.27)
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\sum_{ \forall n \in [0, x[_{\mathbb{S}^{-1}_{Z}} } \!\!\!\! n\;\;\;=\;\;\;\# [ 0, x [_{\mathbb{A}_{\S}} \; \cdot \; ω \cdot \left( x - \frac{ 1 }{ \s } \right) } \]	(SN.AbIn.NU.28)

Ein mir bisher unbekanntes und bemerkenswertes Ergebnis aus unendlichen Summen und aktual unendlichen Anzahlen.

Ebenso für die Summe aller endlichen realen Koeffizienten der Superial-Zahlen von Null bis ausschließlich – oder einschließlich – $ x $ können wir ein Ergebnis finden:

\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \sum_{ \forall a \in [ 0, x [_{\mathbb{A}_{\S}}} \!\! a\;\;\;=\;\;\;\frac{ x^{2} \cdot s }{ 4 \cdot ω } - \frac{ x }{ 2 } } \]	(SN.AbIn.NU.39)
► einblenden
▼ ausblenden
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\sum_{ \forall a \in [ 0, x ]_{\mathbb{A}_{\S}}} \!\! a\;\;\;=\;\;\;\frac{ x^{2} \cdot s }{ 4 \cdot ω } - \frac{ x }{ 2 } + x } \]	(SN.Ein.15)
▲ ausblenden
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\sum_{ \forall a \in [ 0, x ]_{\mathbb{A}_{\S}}} \!\! a\;\;\;=\;\;\;\frac{ x^{2} \cdot s }{ 4 \cdot ω } + \frac{ x }{ 2 } } \]	(SN.Ein.16)

Diese Summe ließ sich vorher nicht explizit in einer aktual unendlichen Zahl ausdrücken, soweit mir bekannt.

In alldem kommen einige interessante Dinge vor, wie wir sehen, die zuvor wohl nicht zu fassen waren: Auch die Anzahl aller endlichen rationalen Zahlen insgesamt und in einem Intervall konnte nach meinem Wissen zuvor nicht durch eine aktual unendliche Zahl ausgedrückt werden. Und auch, wie eben gesagt, dass die Summe der endlichen ganzen Zahlen negativ ist und $ -ω $ entspricht, war mir nicht bekannt.

Ich denke, all dies ist schon etwas ziemlich besonderes und kann Appetit auf mehr machen. Da ist im Folgenden noch einiges faszinierendes zu Entdecken.

Ein Stellenwertsystem
Eine fraktale Struktur

Bei etwas intensiverem Herumspielen fällt einem auf, dass die Superial-Zahlen sich wie ein Stellenwertsystem verhalten. Die Ziffern der Stellen können alle rationalen Zahlen sein, sogar negative. Durch diese Erkenntnis finden wir die Möglichkeit, die Darstellung gegebenenfalls zu verkürzen, wie beispielsweise die folgende:

\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { - \frac{3}{5} \cdot \s^{2} + 25 \cdot \s^{1} + 3,5 \cdot \s^{0} - 7,2 \cdot \s^{-1} \\ \qquad\qquad\qquad\quad\;\;\;=\;\;\;\left\langle - \frac{3}{5} \right\rangle \left\langle 25 \right\rangle \left\langle 3,5 \right\rangle .\!\left\langle -7,2 \right\rangle } \]

(SN.Ein.17)

Zur Kennzeichnung der endlichen, nullten Stelle haben wir zwischen ihr und der minus ersten Stelle einen Punkt gesetzt, wie das im Angelsächsischen hinter der nullten Stelle einer Dezimalzahl üblich ist.

Diese Darstellung verdeutlicht auch, dass es sich bei $ \s $ im Grunde um eine unendlich große Eins oder genauer um eine superial große Eins handelt; und bei $ \s^{-1} $ um eine unendlich kleine Eins oder genauer um eine superial kleine Eins:

\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \s\;\;\;=\;\;\;\s^{1}\;\;\;=\;\;\;\left\langle 1 \right\rangle \left\langle 0 \right\rangle\!.\;\;\;=\;\;\;\left\langle 1 \right\rangle _{1} } \]	(SN.Ein.18)
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { 1\;\;\;=\;\;\;\s^{0}\;\;\;=\;\;\;\left\langle 1 \right\rangle\!.\;\;\;=\;\;\;\left\langle 1 \right\rangle _{0} } \]	(SN.Ein.19)
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \s^{-1}\;\;\;=\;\;\;.\!\left\langle 1 \right\rangle \;\;\;=\;\;\;\left\langle 1 \right\rangle _{-1} } \]	(SN.Ein.20)
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \s + \s^{-1}\;\;\;=\;\;\;\left\langle 1 \right\rangle \left\langle 0 \right\rangle\!.\!\left\langle 1 \right\rangle \;\;\;=\;\;\;\left\langle 1 \right\rangle _{1}\left\langle 1 \right\rangle _{-1} } \]	(SN.Ein.21)
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \s + 1 + \s^{-1}\;\;\;=\;\;\;\left\langle 1 \right\rangle \left\langle 1 \right\rangle\!.\!\left\langle 1 \right\rangle } \]	(SN.Ein.22)

Anstatt eines Punktes kann auch die Potenz der vorstehenden Klammer durch einen Index gekennzeichnet werden.

Ich habe diese unter Umständen etwas kürzere und elegantere Darstellung eingangs nicht benutzt, um die Formeln einfach und verständlich zu halten und damit eine gute Transparenz zu gewährleisten, also um nicht durch zu viel Neues zu verwirren. Nachfolgend werde ich sie jetzt häufiger nutzen.

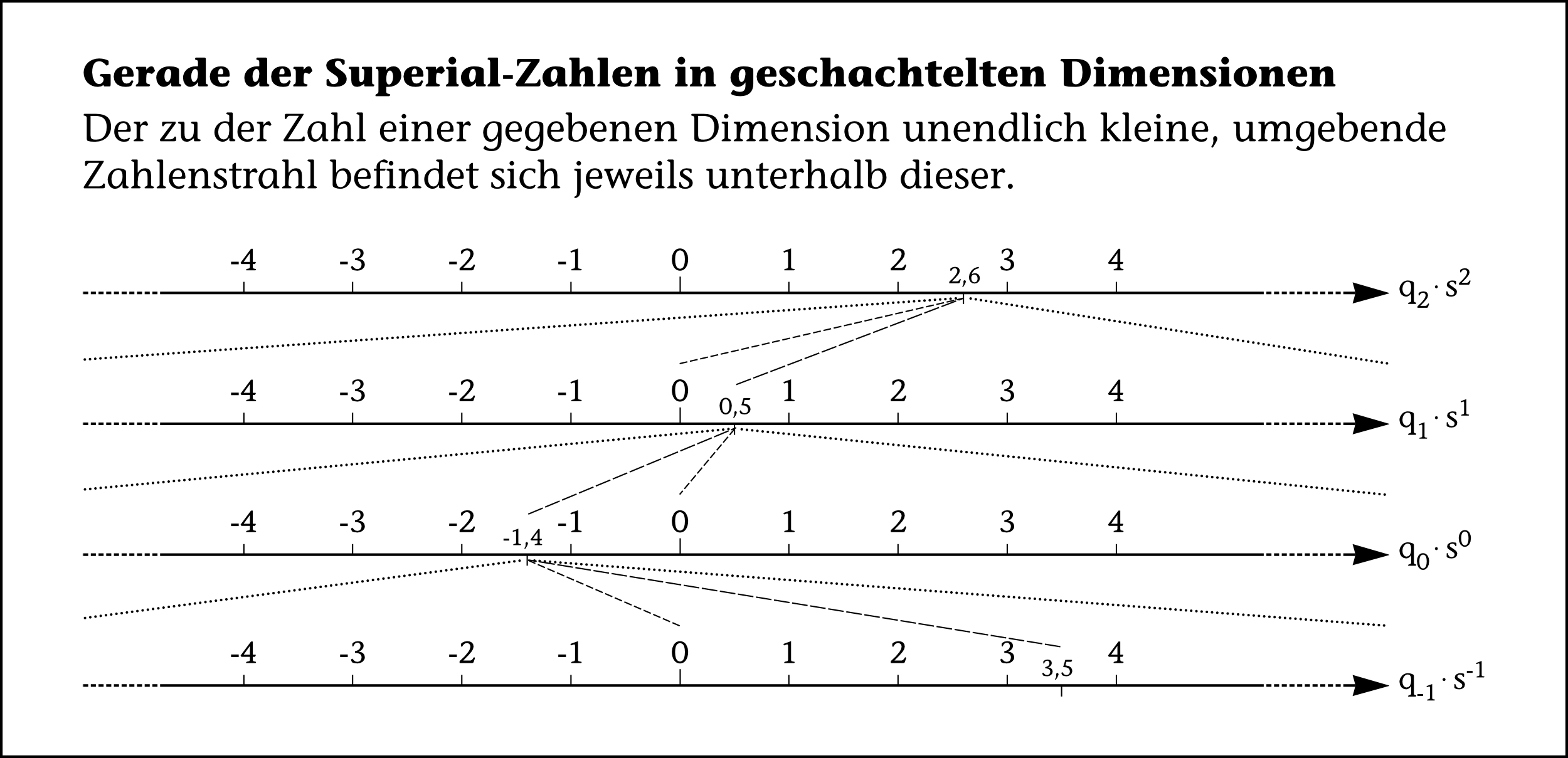
Die Stellenwertsystem-Darstellung verdeutlicht, dass die Superial-Zahlen eine fraktale Struktur besitzen, die sich in jeder Zahlenstelle beziehungsweise Potenzebene von $ s $ wiederholt (siehe ).

Ihre Selbstähnlichkeit bezieht sich darauf, dass die Gerade der endlichen rationalen Zahlen um die unendlich kleinen, superialen Zahlen erweitert wird und auf diese Weise zwischen den endlichen Zahlen noch unendlich viele, unendlich kleine Zahlengeraden verschiedenster Dimensionsgrößen hat. Erstaunlicherweise kennt die Mathematik dadurch jetzt nicht nur orthogonale Dimensionen(Verweis), die senkrecht zueinander stehen, sondern auch unendlich kleine, lineare Dimensionen – superiale Dimensionen –, die sich in fraktaler Weise zwischen unseren endlichen Zahlen verstecken. Auf Basis der superialen Einheit $ \s $ lassen sich folglich eben auch unendlich große, lineare Dimensionen beschreiben. Zwischen denen liegen dann unsere endlichen Zahlen und so fort.

Mit Primzahlen ins Unendliche
Was ist unsere neue superiale Basis $ \s $?

Wir haben nun eine gute Idee, was wir mit der superialen Basis $ s $ anfangen können. So stellt sich schließlich die Frage:

Können wir sagen, was $ s $ genau ist? Wie definieren wir unsere superiale Basis und stiften damit noch mehr Sinn; gewinnen noch mehr Erkenntnis?

Mit dieser wichtigen Frage konfrontierte mich einst ein Hamburger Universitätsprofessor, den ich mit einer von ihm unverlangten E-Mail an ihn und einer darauf folgenden E-Mail Korrespondenz vermutlich ziemlich nervte. Unsere Korrespondenz wurde im Grunde mit dieser Frage und mit einem Hinweis und Ratschlag an mich beendet, den ich nun nicht weiter vertiefen möchte.

Wie dem auch sei, für seine kluge Frage bin ich dem Herrn außerordentlich dankbar! Denn sie hat in mir einen tief gehenden Denkprozess ausgelöst und schließlich zu einer Erkenntnis geführt, deren Tragweite in meinen Augen nicht zu unterschätzen ist.

Primzahlen sind grundlegend für die Antwort
Mit diesen Fragen kommen wir weiter, wenn wir uns mit den stillschweigenden Annahmen beschäftigen, die wir treffen, wenn wir oben mit Hilfe von $ s $ und definieren.

Wir konnten bei der Herleitung des Integrals aus der Ableitung oben schon feststellen, dass wir bezüglich der Ableitung schon stillschweigend oder unbewusst davon ausgegangen sind, es würde unendlich viele unendlich kleine ganze Zahlen geben. Beim Integrieren kommen wir nämlich in die Verlegenheit, in ganzen Schritten all die Differenzen der Ableitung wieder aufzusummieren. Dabei stellt sich die Frage: Wie groß sind diese Schritte und wieviele Schritte sind notwendig, um die ursprüngliche Funktion $ f(x) $ aus der abgeleiteten $ f'(x) $ wieder herzustellen.

Als wir uns damit beschäftigten, kam die Erkenntnis, wir müssten $ x \cdot s $ Schritte in den Funktionswerten von $ f'(x) $ der Größe $ \s^{-1} $ von Null bis ausschließlich $ x $ addieren.

Diese Schritte konnten wir durch Skalierung von ganzen Zahlen von Null bis ausschließlich $ x \cdot s $ erzeugen. Was zum einen die Existenz dieser unendlich großen ganzen Zahlen voraussetzt; und zum anderen, dass sich diese Zahlen nach ihrer Größe ordnen lassen, also linear angeordnet sind.

Welche Eigenschaften muss $ s $ demnach haben, damit ein Produkt von $ s $ mit jeder rationalen Zahl eine ganze Zahl ergibt, auch wenn diese unendlich groß ist?

Rationale Zahlen und ihre Primfaktorzerlegung
(Durch den Beweis der Überrationalitätsvermutung haben sich die Koeffizienten der Superial-Zahlen von den endlichen rationalen Zahlen auf die Koeffizienten der algebraischen Zahlen erweitert, was noch berücksichtigt werden muss.)
Ebenso, wie jede natürliche Zahl größer Eins eine Primfaktorzerlegung hat, so hat im Grunde auch jede rationale Zahl größer Null und ungleich Eins eine Primfaktorzerlegung, wenn wir negative Potenzen der Primzahlen zulassen, wie beispielsweise:

\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \frac{ 250 }{ 567 }\;\;\;=\;\;\;\frac{ 2 \cdot 5^{3} }{ 3^{4} \cdot 7 } } \]	(SN.Ein.23)
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\frac{ 250 }{ 567 }\;\;\;=\;\;\;2 \cdot 3^{-4} \cdot 5^{3} \cdot 7^{-1} } \]	(SN.Ein.24)

Dies kommt daher, weil bekanntermaßen jede rationale Zahl ein Bruch zweier ganzer Zahlen ist. Ausgeschlossen ist natürlich durch Null zu teilen.

Welche Eigenschaft muss die Zahl $ s $ haben, sodass sie multipliziert mit jeder rationalen Zahl immer noch eine ganze Zahl ergibt?

Die Definition von $ s $
Nach meinem Verständnis muss $ s $ eine Primfaktorzerlegung haben, die eine unendlich große Potenz aller endlichen Primzahlen ist. Nur so ist gewährleistet, dass keine Potenz im Produkt einer rationalen Zahl mit $ s $ negativ und dadurch das Produkt eine gebrochene Zahl wird. Und nur dadurch ist gewährleistet, dass wir ein solches Produkt beliebig endlich oft machen können, ohne, dass das Ergebnis endlich werden kann, sondern unendlich groß bleibt.

In $ s $ muss also jede Primfaktorzerlegung einer endlichen ganzen Zahl beliebig endlich oft stecken. Eine Definition von $ s $, die dies explizit umsetzt, finden wir auf der Seite Formale Entwicklung im Abschnitt Die superiale Basis s wird auf natürliche Weise sichtbar und definiert.

Folgendes Primzahlprodukt sollte das einfachste kleinste Produkt aus unendlich vielen Primfaktoren sein, dass diese Bedingung erfüllt, dabei ist $ \mathbb{P} $ die Menge aller endlicher Primzahlen:

\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { s\;\;\;≔\;\;\;\displaystyle \prod_{\forall n \in \mathbb{N}} \left( \prod_{\forall p \in \mathbb{P}} p \right) } \]

(SN.Ein.24)

In diesem Produkt wird erst einmal das Produkt aller endlichen Primzahlen $ 2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 13 \cdot \cdots $ gebildet, um sie alle vorrätig zu haben. Anschließend wird es so oft mit sich selber mal genommen, wie groß die Anzahl der endlichen natürlichen Zahlen ist, um alle Primzahlen auch in einer Potenz vorrätig zu haben, die für alle gleich groß ist, aber so klein wie möglich, dass die Potenz durch keine in rationalen Zahlen mögliche, negative Potenz in einem Produkt mit ihr endlich groß werden kann.

Die hier in der Potenz erzeugte Anzahl wird in der Mengenlehre mit $ ω $ bezeichnet und steht so für die vollständige Induktion. So können wir über das Symbol $ \# $ der Anzahl der Elemente einer Menge, das ich hier auf unendlich große, abzählbare Mengen erweitere, definieren:

\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \mathbb{N} \;\;\;≔\;\;\;\mathbb{N}_{0} } \]	(BO.Ein.8)
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { ω \;\;\;≔\;\;\;\#\mathbb{N} } \]	(SN.Ein.25)
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}s\;\;\;≔\;\;\;\displaystyle \left( \prod_{\forall p \in \mathbb{P}} p \right)^{ω} } \]	(SN.Ein.26)

Wie Formel BO.Ein.8 definiert, setze ich voraus, dass die natürlichen Zahlen die Null enthalten. Den Grund dafür verdeutliche ich im Abschnitt .

Für das Primzahlprodukt von $ s $ ergibt sich also, wie eben beschrieben, eine mit unendlich mal unendlich vielen Primzahlen gefüllte Fläche der folgenden Art:

\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}s\;\;\;=\;\;\;\prod_{\forall n \in \mathbb{N}} \left( 2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 13 \cdot 17 \cdot 19 \cdot 23 \cdot \cdots \right) } \]	(SN.Ein.27)
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}s\;\;\;=\;\;\;(2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 13 \cdot 17 \cdot 19 \cdot 23 \cdot \cdots )_{1} \\ \qquad\qquad\quad\; \cdot ( 2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 13 \cdot 17 \cdot 19 \cdot 23 \cdot \cdots )_{2} \\ \qquad\qquad\quad\; \cdot ( 2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 13 \cdot 17 \cdot 19 \cdot 23 \cdot \cdots )_{3} \\ \qquad\qquad\quad\; \;\;\;\; \vdots \\ \qquad\qquad\quad\; \cdot ( 2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 13 \cdot 17 \cdot 19 \cdot 23 \cdot \cdots )_{n \in \mathbb{N}} \\ \qquad\qquad\quad\; \;\;\;\; \vdots } \]	(SN.Ein.28)
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}s\;\;\;=\;\;\;\left( 2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 13 \cdot 17 \cdot 19 \cdot 23 \cdot \cdots \right)^{ω} } \]	(SN.Ein.29)

Die Veränderung der Primfaktorzerlegung von $ s $ durch rationale Koeffizienten
Mit Hilfe der neuen Theorie der Biordinalzahlen können wir auch Zahlen wie $ ω - n $, mit $ n \in \mathbb{N} $, darstellen und damit die Veränderung der Primzahlpotenzen des unendlichen Primzahl-Flächenprodukts durch rationale Koeffizienten mit biordinalen Potenzen angeben:

\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \frac{2}{9} \cdot s\;\;\;=\;\;\;2^{ ω + 1} \cdot 3^{ ω - 2} \cdot \left( 5 \cdot 7 \cdot 11 \cdot 13 \cdot 17 \cdot 19 \cdot 23 \cdot \cdots \right)^{ω} } \]

(SN.Ein.31)

Hier können wir sehen, dass $ s $ durch Multiplikation mit endlich beliebig vielen rationalen Zahlen immer unendlich groß bleibt, also seine superiale Dimension nicht verändert. Denn dadurch werden, aufgrund der Primfaktorzerlegung endlicher ganzer Zahlen, immer nur natürliche Zahlen auf die jeweiligen Potenzen addiert oder von ihnen abgezogen. Da für jede natürliche Zahl $ n $ die Differenz $ ω - n $ immer unendlich groß bleibt, kann kein rationaler Koeffizient $ q $ einer endlich ganzzahligen Potenz $ z $ von $ s $, also unser folgendes $ s^z $, in eine andere Potenzebene bringen:

\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \left( \nexists q_{z} \in \mathbb{Q}^{+} \right) \left( \forall z \in \mathbb{Z} \right) \left( \forall q_{z-1} \in \mathbb{Q}^{+} \right) \\ \qquad\qquad\qquad \left[\; q_{z} \cdot s^{z}\;\;\;<\;\;\;q_{z-1} \cdot s^{z-1} \;\right] } \]	(SN.Ein.32)
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \left( \nexists q_{z} \in \mathbb{Q}^{+} \right) \left( \forall z \in \mathbb{Z} \right) \left( \forall q_{z+1} \in \mathbb{Q}^{+} \right) \\ \qquad\qquad\qquad \left[\; q_{z} \cdot s^{z}\;\;\;>\;\;\;q_{z+1} \cdot s^{z+1} \;\right] } \]	(SN.Ein.33)

Die Potenz $ z $ von $ s $ dominiert den Koeffizienten $ q $ bezüglich der Größe in der Anordnung und ist der Grund für die lexikografische Ordnung der Superial-Zahlen.

Diese Eigenschaft ist generell sehr bemerkenswert und tatsächlich auch durch die Definition von $ s $ über das unendliche Primzahl-Flächenprodukt gewährleistet. Weiteres zur Dominanz der Potenzen von $ s $ untersuchen wir im Abschnitt Zahlen und Mengen im Unendlichen.

Primzahlen haben eine Verbindung ins Unendliche
Die neu entdeckten, unendlich großen Primfaktorzerlegungen offenbaren einen tiefen Zusammenhang der endlichen Primzahlen mit dem Unendlichen über die rationalen Zahlen.

Primzahlprodukt-Vermutung
(Der Beweis der Primzahlprodukt-Vermutung muss noch berücksichtigt werden.)
Im spielerischen Umgang und in tieferen Analysen der Zusammenhänge kommt die Vermutung auf, dass das Produkt der einfachen Potenz aller endlichen Primzahlen, also eine Zeile des Primzahl-Flächenprodukts, der Anzahl der natürlichen Zahlen $ ω $ entspricht:

\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { ω\;\;\;\overset{?}{=}\;\;\;ω_{\forall p}\;\;\;≔\;\;\;2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 13 \cdot 17 \cdot 19 \cdot 23 \cdot \cdots } \]	(SN.PP.6)
\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}s\;\;\;=\;\;\;\left( 2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 13 \cdot 17 \cdot 19 \cdot 23 \cdot \cdots \right)^{ω} \\ \qquad\quad\;\;\;\;=\;\;\;\left( ω_{\forall p} \right)^{ω}\;\;\;\overset{?}{=}\;\;\;ω^{ω} } \]	(SN.PP.7)

Die Primzahlprodukt-Vermutung findet im Abschnitt Ausgangspunkt der Primzahlprodukt-Vermutung eine nähere Begründung. Dort wird aufgrund des unendlich ganzzahligen Zählens innerhalb der Superial-Zahlen unter anderem erkannt, dass die Anzahl aller endlichen ganzen Zahlen $ 2 \cdot ω $ ein ganzzahliger Teiler von $ \s $ sein muss. Daher muss $ ω $ ein ganzzahliger Teiler von $ \frac{ \s }{ 2 } $ sein, also ein ganzzahliges Teilprodukt.

Damit muss $ ω $ ein unendlich großer Teil des Primzahlprodukts von $ \s $ sein. Und bei näherer Analyse stellen wir auch fest, dass es sich um einen unendlich großen Teil des Primzahlprodukts im horizontalen Bereich aller unterschiedlichen Primzahlen handeln muss.

In unserem Beweis der Primzahlprodukt-Vermutung zeigen wir zusätzlich, dass es nur sein kann, dass die Primfaktorzerlegung von $ ω $ endliche Primzahlen von Beginn an und ohne Lücke enthalten muss. Und von diesen dann unendlich viele, was zusammengefasst bedeutet, einfach alle endlichen Primzahlen.

Überrationalitätsvermutung
(Durch den Beweis der Überrationalitätsvermutung haben sich die Koeffizienten der Superial-Zahlen von den endlichen rationalen Zahlen auf die Koeffizienten der algebraischen Zahlen erweitert, was noch berücksichtigt werden muss.)
Eine weitere Vermutung, die der Primfaktorzerlegungen von $ \s $ entspringt, dreht sich um die Frage, ob der positive reelle Anteil von algebraischen Zahlen durch einen von mir so genannten überrationalen Bruch dargestellt werden kann.

Ein überrationaler Bruch ist ein Bruch, der im Nenner und im Zähler unendlich große, teilerfremde Zahlen hat, deren Primfaktorzerlegung aus unendlich vielen endlichen Primzahlen endlich ganzzahliger Potenzen besteht. Dann wäre ein Produkt eines überrationalen Bruchs mit $ \s $ ebenfalls unendlich groß und ganzzahlig.

Zu den algebraischen Zahlen gehören auch ganzzahlige Wurzeln natürlicher Zahlen, wie $ \sqrt{2} $, womit dann beispielsweise $ \sqrt{2} \cdot \s $ ganzzahlig wäre.

Sollte die Überrationalitätsvermutung sich als wahr erweisen, dann wäre dies ebenfalls eine sehr bemerkenswerte Eigenschaft der Superial-Zahlen, die uns neue Informationen über algebraische Zahlen geben würde und so ein wichtiger Beitrag zur Zahlentheorie wäre. Denn so würde auch eine bessere Differenzierung zwischen den irrationalen und den transzendenten Zahlen ermöglicht.
(Durch den Beweis der Überrationalitätsvermutung haben sich die Koeffizienten der Superial-Zahlen von den endlichen rationalen Zahlen auf die Koeffizienten der algebraischen Zahlen erweitert, was noch berücksichtigt werden muss.)

Die Erweiterung der Arithmetik ins Unendliche

Die Superial-Zahlen erweitern die uns bekannte Arithmetik ins Aktual-Unendliche, wobei sehr viele ihrer Regeln nicht nur für ihre endlichen Zahlen gelten, sondern auch in der Erweiterung:

Unendliche Untermengen der Zahlen
Es werden auch die Untermengen der Zahlen erweitert. So gibt es zum Beispiel natürliche, ganze, gerade und ungerade Superial-Zahlen.

Unendliche Primzahlen
Auch eine Erweiterung der Primzahlen kann auf diese Weise definiert werden und man erhält die Menge $ \mathbb{S}_P $ der superialen Primzahlen. Zum Beispiel sind die Zahlen $ s - 1 $ und $ s + 1 $ unendlich große Primzahlen, weil sie durch keine endliche Primzahl ganzzahlig teilbar sind und auch keine andere Zahl in diesem System gefunden werden kann, die diese Zahlen ganzzahlig teilt. Die Zahlen $ s \pm 2 $ sind hingegen beide durch $ 2 $ teilbar, also keine Primzahlen.

Diese Erweiterung der Primzahlen ins Unendliche ist interessant, weil sie die Verteilung der Primzahlen im Unendlichen beleuchtet und so auch neue Einsichten für die endlichen Primzahlen verspricht.

Rechnen im Unendlichen
Auch das beliebige vorwärts und rückwärts Zählen, die Addition, die Multiplikation und deren Umkehrrechenarten, die Subtraktion und die Division, werden ins Unendliche erweitert. Ebenso gibt es weiter den Betrag einer Zahl, das Modulo und den Rest einer Teilung.

Gesetze im Unendlichen
Auch bleiben das Kommutativgesetz, das Assoziativgesetz und das Distributivgesetz erhalten.

Anordnung im Unendlichen
Und die Superial-Zahlen sind, wie gesagt, nach ihrer Größe lexikografisch angeordnet, unter Berücksichtigung ihrer Potenzen von $ \s $.

Eine unerwartete Verbindung der rationalen Zahlen mit dem Zählen
Das natürliche Zählen spiegelt sich in den natürlichen Superial-Zahlen $ \mathbb{S}_N $ wider. Diese enthalten alle endlichen rationalen Zahlen in ihren Koeffizienten der Potenzen von $ s $.

Nun wissen wir, dass wir rationale Zahlen nicht ihrer Größe nach aufzählen können, weil sie von ihrer Anordnung her dicht sind. Interessanter Weise zählen wir in den natürlichen Superial-Zahlen die rationalen Zahlen ihrer Größe nach, als Koeffizienten der Potenzen von $ \s $, implizit mit.

Denn wir zählen:

\[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \qquad\; 0,\; 1,\; 2,\; 3,\; \cdots \\ \quad\quad\; \vdots \\ \quad \cdots \frac{1}{3} \cdot s - 2,\; \frac{1}{3} \cdot s - 1,\; \frac{1}{3} \cdot s,\; \frac{1}{3} \cdot s + 1,\; \frac{1}{3} \cdot s + 2, \cdots \\ \quad\quad\; \vdots \\ \quad \cdots \frac{1}{2} \cdot s - 2,\; \frac{1}{2} \cdot s - 1,\; \frac{1}{2} \cdot s,\; \frac{1}{2} \cdot s + 1,\; \frac{1}{2} \cdot s + 2, \cdots \\ \quad\quad\; \vdots \\ \quad \cdots \frac{3}{2} \cdot s - 2,\; \frac{3}{2} \cdot s - 1,\; \frac{3}{2} \cdot s,\; \frac{3}{2} \cdot s + 1,\; \frac{3}{2} \cdot s + 2, \cdots \\ \quad\quad\; \vdots } \]

(SN.Ein.34)

Und so fort.

Dort wo drei vertikale Punkte ›⋮‹ stehen, werden alle von der Größe her dazwischen liegenden rationalen Koeffizienten mitgezählt. Die Superial-Zahlen bringen so die rationalen Zahlen mit dem Zählen von natürlichen und ganzen Zahlen in Verbindung.

Weitreichender Erkenntnisgewinn

Die Erkenntnisse, die wir mit den Superial-Zahlen und ihren systematischen Vorgängern, den Biordinalzahlen, jetzt schon erhalten, sind also weitreichend. Und wir dürfen erwarten, dass noch ein ganzes Reich an interessanten und erstaunlichen Erkenntnissen zu erforschen und zu schöpfen ist.

Zahlentheorie der Analysis
Eine direkte Verbindung von Analysis und Zahlentheorie
Über die Definition der und der durch die aktual unendlichen Superial-Zahlen wird die Analysis nun ganz direkt mit der Zahlentheorie verbunden. Denn hierdurch werden nicht „nur“ die Primzahlen mit analytischen Methoden untersucht, sondern die analytischen Methoden werden auf Basis eines unendlichen Produkts von Primzahlen definiert.

So spielen jetzt die Primzahlen auf beiden Seiten eine Rolle: Zur Analyse, als neue Zahlentheorie der Analysis, wie auch als Objekte der Analyse in der bekannten analytischen Zahlentheorie. Dies hat weitreichende Konsequenzen, die beispielsweise zum Beweis der Riemannschen Vermutung einen Beitrag leisten könnten.

Darüber hinaus wird eine einfache und anschauliche Definition von Ableitungen und Integralen möglich.

Feine Differenzierung des Aktual-Unendlichen
Durch die Definition der superialen Einheit $ \s $ als unendliches Primzahlprodukt erhalten die Superial-Zahlen den Mehrwert, dass sich das Aktual-Unendliche nach den gewohnten Regeln der Arithmetik behandeln und differenzieren lässt. Wichtige Elemente der Arithmetik, wie beispeilsweise natürliche, ganze, gerade und ungerade Zahlen sowie Primzahlen, lassen sich so im Unendlichen untersuchen. Dies hat auch Rückwirkung auf die Betrachtung des Endlichen. Denn so ergeben sich unter anderem neue Möglichkeiten die Verteilung der Primzahlen unter den großen endlichen natürlichen Zahlen besser zu verstehen. Auch die Primfaktorzerlegung und die Ordnung der rationalen Zahlen sind so noch einmal neu zu betrachten.

→

Grundlagen
Grundlagen

Fragestellungen und perspektivischer Erkenntnisgewinn
Fragestellungen und perspektivischer Erkenntnisgewinn

Fußnoten
Fußnoten

Stand 14. Dezember 2024, 13:00 CET.

• Permanente Links:
  (Klicke auf die Archivlogos
  zum Abruf und Ansehen
  der Archive dieser Seite.)

• 

• archive.today

  webpage capture

• ^{Crowdfunding:}