| ← |
Eigenschaften
Welche Erkenntnisse können wir aus den Superial-Zahlen lernen?
Die Superial-Zahlen, als aktual unendliche algebraische Gruppe, deren Basis über ein unendliches Primzahl-Produkt definiert ist, haben eine ganz besondere Struktur. Ihre Struktur verbindet über die Ordinalzahlen rationale und algebraische Zahlen tief mit den Primzahlen, den natürlichen Zahlen, den ganzen Zahlen und erweitert all diese ins Aktual-Unendliche.
Dieser Zusammenhang eröffnet ganz neue Perspektiven auf die Zahlentheorie und eröffnet auf diese Weise auch konkret die Anzahlen von Elementen in diesen Mengen und deren Teilmengen mit aktual unendlichen Zahlen zu beschreiben. Darüber können wir Summen der Elemente von diesen unendlichen Mengen bestimmen und gelangen schließlich zu einer neuen Definition des Integrals und der Ableitung über aktual unendliche Zahlen, die ohne den Limes auskommen.
Diese Summen können oft nur über die von mir entdeckten, geschöpften und auf diesen Seiten entwickelten Biordinalzahlen ausgedrückt werden. Gleiches gilt auch für die Beschreibung der hierfür notwendigen aktual unendlichen Potenzen der Primzahlen.
Die besonderen Eigenschaften der Superial-Zahlen, die auf dieser Seite näher untersucht werden, versprechen uns tiefe neue Einblicke in die Struktur der Zahlen, inklusive der transzendenten Zahlen, und begründen damit die Zahlentheorie der Analysis.
| → |
|
Was lernen wir über rationale beziehungsweise algebraische Zahlen |
|
| ← |
| ▾ | Notizen |
Nachkommastellen
• Wir können lernen, dass die rationale Zahl $ ⅓ = 0,\!33333\overline{3} = 0 \cdot 10^{0} + 3 \cdot 10^{-1} + 3 \cdot 10^{-2} + 3 \cdot 10^{-3} + \cdots $ oder auch die algebraische Zahl $ φ $ nur Nachkommastellen haben, die alle endliche Werte haben, also endliche negative Potenzen haben, auch, wenn es unendlich viele sind. Dies muss so sein, weil es sonst einen Übertrag in die nächst tiefere Stelle der Superial-Zahl gibt.
– Das ergibt sich aus den sinnvollen Koeffizienten der Superial-Zahlen.
(In Arbeit …)
| → |
|
| |
$ \mathbb{S} $ ist ein angeordneter Körper |
|
| ← |
|
(Durch den Beweis der Überrationalitätsvermutung haben sich die Koeffizienten der Superial-Zahlen von den endlichen rationalen Zahlen auf die Koeffizienten der algebraischen Zahlen erweitert, was noch berücksichtigt werden muss.)
Die Menge der Superial-Zahlen $ \mathbb{S} $ ist in vielerlei Hinsicht etwas Besonderes.
Wir können nämlich für zwei Superial-Zahlen, die nicht gleich sind, immer herausfinden, welche größer als die andere ist, weil sie eine lexikografische Ordnung haben. $ \mathbb{S} $ ist nämlich ein angeordneter Körper. (Dies ist zu beweisen: die Körpereigenschaft und das Angeordnetsein.)
Ist $ \mathbb{S} $ ein archimedisch angeordneter Körper?
Es stellt sich die Frage, ob die Superial-Zahlen, also die Menge $ \mathbb{S} $, auch ein archimedisch angeordneter Körper sind.
Das archimedische Axiom besagt,
dass in einem archimedisch angeordneten Körper $ \mathbb{K} $ immer eine natürliche Zahl existiert,
die als Faktor jede Zahl einer Menge größer machen kann als eine andere Zahl der gleichen Menge:
Es besagt also, dass alle Elemente des archimedisch angeordneten Körpers endlich sind, es jedoch unendlich viele davon gibt.
Dies gilt aber nicht für den angeordneten Körper der Superial-Zahlen, weil es Elemente einer Untermenge $ x \in \mathbb{Q} $ gibt, für das es keinen Faktor in $ \mathbb{N} $ gibt, um beides als Produkt größer als $ \s $ zu machen:
Denn $ \mathbb{S} $ enthält zum Beispiel mit $ q \cdot \s $ Elemente, die größer als jede endliche natürliche Zahl und damit unendlich groß sind.
Wie wir daran sehen, handelt es sich bei den Superial-Zahlen um eine ganz andere Menge, als bei Mengen endlicher Zahlen.
Gibt es eine größere geordnete Teilmenge der Superial-Zahlen, die auch unendliche Elemente oder Elemente mit solchen Anteilen, beinhaltet, die ein archimedisch angeordneter Körper ist?
(In Arbeit …)
Wie kann das archimedische Axiom für eine möglichst große Teilmenge von $ \mathbb{S} $ erfüllt werden?
Es scheint mir, dass dies erfüllt wird, wenn es keine unendlich großen Summanden in den Elementen der Menge gibt.
Sowohl $ x $ als auch $ y $ müssen zwischen den endlichen Zahlen liegen:
In Anlehnung an die Definition der Menge aller Superial-Zahlen in Formel SN.Fo.1 können wir diese Menge auch so schreiben:
So enthalten diese Superial-Zahlen keine Summanden mit Potenzen von $ \s $, die größer als Null sind.
(In Arbeit …)
Aber $ \mathbb{S} $ ist bezüglich der natürlichen Superial-Zahlen $ \mathbb{S}_N $ ein archimedisch angeordneter Körper
(In Arbeit …)
(In Arbeit …)
(In Arbeit …)
(In Arbeit …)
(In Arbeit …)
(In Arbeit …)
| → |
|
| |
Die Struktur von $ \s $ |
|
| ← |
|
Die Beschäftigung mit der Struktur von $ \s $ ist sehr ergiebig in Bezug auf weitere tiefe Erkenntnisse.
Inhalt
| → |
|
| → |
|
| → |
|
| → |
|
| → |
|
Was lernen wir über die Größe von $ ω $ und die Struktur von $ \s $ anhand der Frage der Vorgänger?
| ▾ | Notizen |
• Können wir die Anzahl der rationalen Zahlen (über den Calkin-Wilf-Baum(Verweis)) oder der reell algebraischen Zahlen quantifizieren?
Jede natürliche Superial-Zahl $ n $ hat so viele Vorgänger in $ \mathbb{S}_{\N} $, wie sie selber groß ist, wie bei den endlichen natürlichen Zahlen. Dies ist anders, als bei den von mir ebenfalls entdeckten und erforschten, auch ins Aktual-Unendliche gehenden Biordinalzahlen: Aktual unendliche Biordinalzahlen haben interessanter Weise mehr Vorgänger als ihr Wert groß ist. In mancherlei anderen Punkten können wir erkennen, dass sie die noch nicht so perfekten Vorläufer der Superial-Zahlen sind. Mathematisch gesehen sind die Biordinalzahlen eine Erweiterung der Ordinalzahlen zu einem algebraischen Ring.
Demnach hat $ \s $ also so viele Vorgänger, wie das Primzahl-Flächenprodukt groß ist. Interessanterweise ist das , obwohl es sich trotz gleicher Werte $ \s = ω^{ω} $ um unterschiedliche Strukturen handelt. Die Anzahl der Vorgänger von $ \s $ ist dann:
| • |
Die Anzahl aller reell algebraischen Koeffizienten $ a $ von $ \s $, für die gilt: $ 0 \leq a < 1 $. |
| • |
Multipliziert mit $ 2 ω $ für die Anzahl der endlichen ganzen Zahlen, siehe ›Eine fundamentale Asymmetrie‹, die ja zu jedem Koeffizienten addiert – und im Falle der negativen natürlich dann abgezogen – werden. Wobei im Falle von $ a = 0 $ nur natürliche Zahlen addiert und im Falle von $ a = 1 $ nur negative ganze Zahlen addiert, also effektiv abgezogen, werden. |
So formulieren wir die Vorgänger von $ \s $ folgendermaßen:
Das Intervall der Vorgänger der superialen Einheit ist im Detail
unter Berücksichtigung der unterschiedlichen Fälle.
Für die Anzahl der Vorgänger finden wir dann:
Seien $ \rbrack a, b \lbrack_{\mathbb{A}_{\S}} $ und $ \lbrack a, b \lbrack_{\mathbb{A}_{\S}} $ Intervall-Mengen aus $ \mathbb{A}_{\S} $,
dann ergibt sich $ \s $, nach vorstehendem Gedanken, zu
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \s\;\;\;=\;\;\;\# \mathbb{N} + \# \left( ] 0, 1 [_{\mathbb{A}_{\S}} \right) \cdot \# \mathbb{Z} + \# \mathbb{Z^{-}} } \] | (SN.Ei.S.L.2) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \# \mathbb{Z}\;\;\;=\;\;\;\# \mathbb{N} + \# \mathbb{Z^{-}} } \] | (SN.Ei.S.L.3) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}\s\;\;\;=\;\;\;\# \mathbb{Z} + \# \left( ] 0, 1 [_{\mathbb{A}_{\S}} \right) \cdot \# \mathbb{Z} } \] | (SN.Ei.S.L.4) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\s\;\;\;=\;\;\;\left( 1 + \# \left( ] 0, 1 [_{\mathbb{A}_{\S}} \right) \right) \cdot \# \mathbb{Z} } \] | (SN.Ei.S.L.5) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\s\;\;\;=\;\;\;\# \left( [ 0, 1 [_{\mathbb{A}_{\S}} \right) \; \cdot \; \# \mathbb{Z} } \] | (SN.Ei.S.L.6) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\s\;\;\;=\;\;\;\# \left( [ 0, 1 [_{\mathbb{A}_{\S}} \right) \; \cdot \; 2 ω } \] | (SN.Ei.S.L.7) | ||
was der Anzahl aller sinnvollen Koeffizienten der Superial-Zahlen entspricht,
die, nach unserer Vermutung, alle reell algebraischen Zahlen sind.
Denn mit
sind alle sinnvollen Koeffizienten, ohne Redundanzen – also Doppelungen – und Lücken, definiert und es folgt daraus
weil es in den sinnvollen Koeffizienten $ \mathbb{A}_{\S} $ das Interval $ \lbrack 0, 1 \lbrack_{\mathbb{A}_{\S}} $ für jede ganze Zahl in $ \mathbb{Z} $ gibt und sie damit vollständig beschrieben sind.
So gilt dann auch, nun doppelt bestätigt,
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\# \left( [ 0, 1 [_{\mathbb{A}_{\S}} \right)\;\;\;=\;\;\;\frac{ \s }{ 2 ω } } \] | (SN.Ei.S.L.12) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\# \left( [ 0, 1 [_{\mathbb{A}_{\S}} \right)\;\;\;=\;\;\;\frac{ ω^{ω} }{ 2 ω } } \] | (SN.Ei.S.L.13) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\# \left( [ 0, 1 [_{\mathbb{A}_{\S}} \right)\;\;\;=\;\;\;\frac{ ω^{ω - 1} }{ 2 } \;\; , } \] | (SN.Ei.S.L.14) | ||
nach Umformung und mit Hilfe von Formel SN.PP.174.
Hier muss es sich um eine ganze Zahl handeln, weil dies die Anzahl der Elemente einer Menge beschreibt, die immer ganz ist, womit nachfolgend diese Erkenntnis ein wichtiger Hinweisgeber zur und zentraler Baustein der Primzahlprodukt-Vermutung ist.
Ausgangspunkt der Primzahlprodukt-Vermutung
Und wir können sogar noch weiter gehen und feststellen, dass $ ω $ seine Primfaktoren mit $ \s $, siehe Formel SN.Ein.26, teilen muss, wenn die Anzahl der sinnvollen Koeffizienten in $ \lbrack 0, 1 \lbrack_{\mathbb{A}_{\S}} = \frac{ \s }{ 2 ω } $ aus Formel eine ganze Zahl ist. Weiter ist klar, dass $ ω $ aktual unendlich groß ist. Es kann also nur ein Produkt aus unendlich vielen endlichen Primzahlen sein.
Doch welches Teilprodukt von $ \s $ ist $ ω $, wenn klar ist, dass $ \s $ unendlich viel größer ist als $ ω $? Denn schon die Potenz oder der Turm der kleinsten Primzahl $ 2^{ω} $ im Primzahl-Flächenprodukt von $ \s $ ist definitiv sehr viel größer als $ ω $. Die einzelnen und kombinierten Türme aller Primzahlen $ p_{i}^{ω} $, mit $ p_{i} \in \mathbb{P} $, können so nicht als Faktoren in $ ω $ enthalten sein.
Das aktual unendlich große Primzahlprodukt, dass auf den ersten Blick bleibt, um $ ω $ darzustellen, ist schlicht die Zeile, die alle endlichen Primzahlen enthält, und lässt vermuten, dass $ ω \overset{?}{=} 2 \cdot 3 \cdot 5 \cdot 7 \cdot \cdots $ ist. Aber auch dieses Produkt erscheint auf den ersten Blick viel größer als die vollständige Induktion zu sein, die ja mit $ ω $ ausgedrückt wird. Im Beweis der Primzahlprodukt-Vermutung gelingt es uns tatsächlich zu zeigen, dass wirklich $ ω = 2 \cdot 3 \cdot 5 \cdot 7 \cdot \cdots $ gilt.
Erklärung der Anzahl der endlichen ganzen Zahlen durch ihren ontologischen Ursprung in der Struktur der Biordinalzahlen
Formulierung der Entstehung der negativen ganzen Zahlen durch Rückwärtszählen, ohne Umkehrung der Zählrichtung
Die vorstehend gemachten Aussagen sind entscheidend davon abhängig, wieviele endliche ganze Zahlen es gibt. Dies bestimmt zum einen, ob sich wirklich plausibel eine ganze Anzahl an sinnvollen Koeffizienten der Superial-Zahlen in $ \lbrack 0, 1 \lbrack_{\mathbb{A}_{\S}} $ ergibt, sodass wir keinen logischen Bruch und damit einen Widerspruch erhalten. Und damit wird bestimmt, ob wir sagen können, dass $ ω $ gemeinsame Teiler mit $ \s $ haben muss.
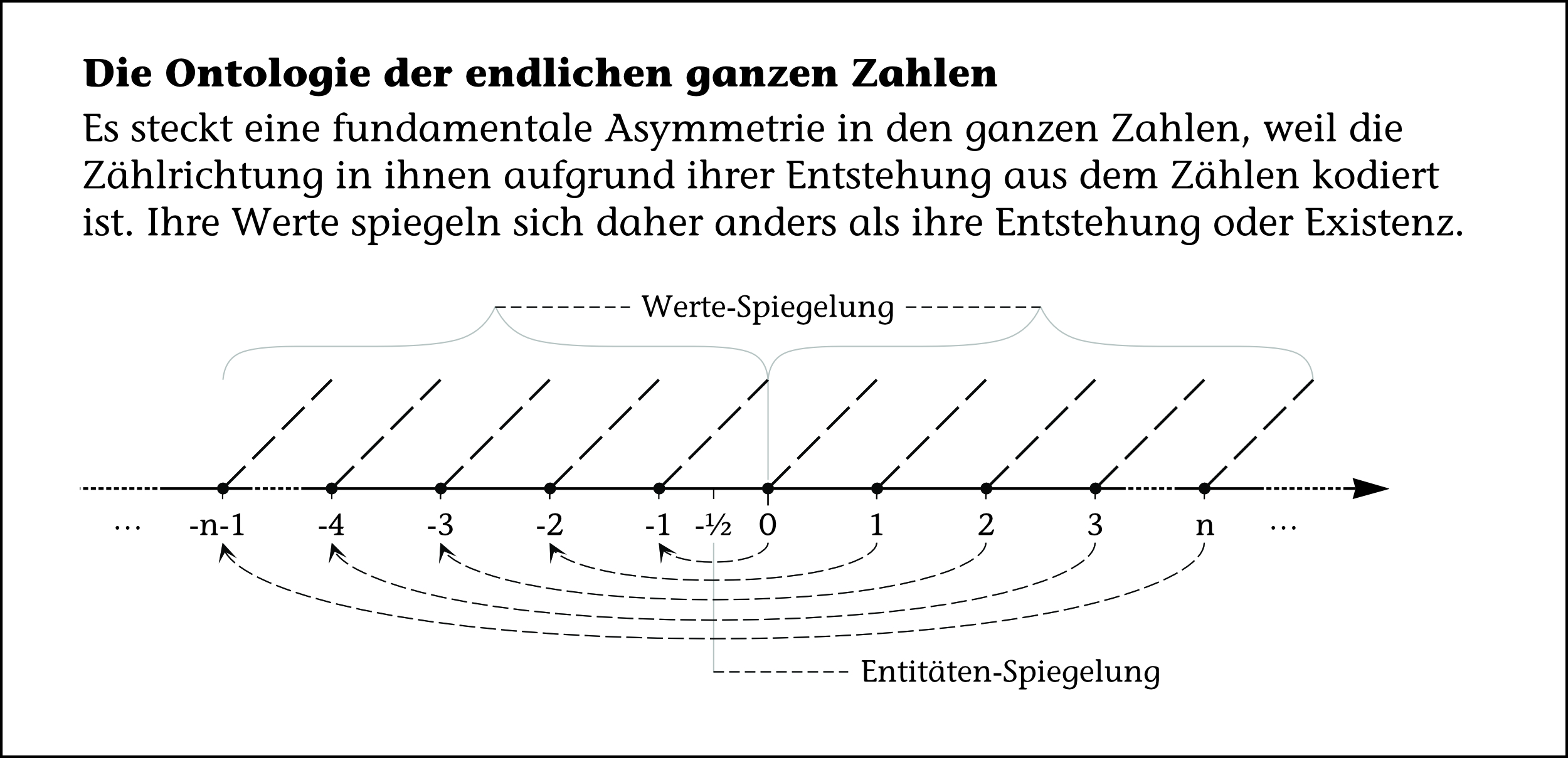
Dies ist einer der Gründe, weswegen ich mich mit den Ordinalzahlen beschäftigt, diese auf die Biordinalzahlen erweitert und ein Stück weit erforscht habe. Darauf basierend haben wir eine fundamentale Asymmetrie herausgearbeitet, die der von uns gefundenen und oben verwendeten Anzahl der endlichen ganzen Zahlen $ 2 ω $ zugrunde liegt.
Diese Anzahl der endlichen ganzen Zahlen ergibt sich wegen der auch im Negativen bleibenden Zählrichtung, die auch dort in Richtung der größer werdenden, und schließlich positiven Zahlen, ausgerichtet bleibt, weil alle Zahlen letztendlich aus dem Zählen hervorgehen. Siehe dazu auch den ›Zähloperator‹ in der ›Operialtheorie‹.
Um auszudrücken, dass jeder negative sinnvolle Koeffizient der Superial-Zahlen Teil eines an einer negativen ganzen Zahl hängenden Zahlenintervalls ist, wo jedes negative Zahlenintervall jeweils aus einem Zahlenintervall an einer natürlichen, also positiven Zahl oder der Null entsteht, berücksichtigen wir im Ansatz die ontologische Vorstellung, dass es sich bei Zahlen quasi um Sägezähne – oder spezielle Wellen – von einer Zahl zur nächsten handelt. Diese Sägezähne hängen in Zählrichtung an den ganzen Zahlen.
|
Die negativen Zahlen entstehen also eigentlich nicht durch eine Spiegelung all dieser Sägezähne an der Null, sondern durch deren jeweils einzelne Verschiebung. Bei einer Spiegelung an der Null wäre die Null auch strukturell gedoppelt – ontologisch redundant –, was keinen Sinn macht, und die Sägezähne drehten sich um, was, wie gesagt, ebenfalls unsinnig erscheint, weil es eine Umkehrung der Zählrichtung bedeutete.
Dieser Zusammenhang soll sich ganz korrekt in der Struktur der ersten Formulierung der Entstehung der negativen Sägezahnintervalle von $ \mathbb{A}_{\S}^{-} $ ausdrücken, die wir auf Basis der Formel ansetzen:
Die Intervalle $ u $, die zwischen den ganzen Zahlen liegen, hängen an der vorstehenden linksseitigen ganzen Zahl und werden auf diese Weise mit verschoben. Daher steht quasi am „Beginn“ der endlichen negativen ganzen Zahlen auch der Punkt einer ganzen Zahl, was eben der Grund dafür ist, dass es eine endliche negative ganze Zahl mehr geben muss, als positive, ohne die Null (siehe ). Denn das Zählen ist die Grundlage aller Zahlen.
Wir formen die Verschiebung vereinfachend um und erhalten:
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\mathbb{A}_{\S}^{-}\;\;\;=\;\;\;\left\{\; x\;~\middle|~\;\left( \forall n \in \mathbb{N} \right) \left( \forall u \in [ 0, 1 [_{\mathbb{A}_{\S}} \right) \\ \qquad\qquad\qquad\qquad\quad\;\;\, \left[\; x = \left( n - 2 n - 1 \right) + u \;\right] \;\right\} } \] | (SN.Ei.S.G.2) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\mathbb{A}_{\S}^{-}\;\;\;=\;\;\;\left\{\; x\;~\middle|~\;\left( \forall n \in \mathbb{N} \right) \left( \forall u \in [ 0, 1 [_{\mathbb{A}_{\S}} \right) \\ \qquad\qquad\qquad\qquad\quad\;\;\, \left[\; x = \left( - n - 1 \right) + u \;\right] \;\right\} } \] | (SN.Ei.S.G.3) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\mathbb{A}_{\S}^{-}\;\;\;=\;\;\;\left\{\; x\;~\middle|~\;\left( \forall n \in \mathbb{N} \right) \left( \forall u \in [ 0, 1 [_{\mathbb{A}_{\S}} \right) \\ \qquad\qquad\qquad\qquad\quad\, \left[\; x = - \left( n + 1 \right) + u \;\right] \;\right\} } \] | (SN.Ei.S.G.4) | ||
Mit Hilfe der Formeln und BO.Ein.NE.6 folgt dann:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \# \mathbb{N}\;\;\;=\;\;\;ω } \] | (BO.Ein.NE.6) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}\# \mathbb{A}_{\S}^{-}\;\;\;=\;\;\;\# \left( [ 0, 1 [_{\mathbb{A}_{\S}} \right) \, \cdot \; ω } \] | (SN.Ei.S.G.5) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\# \mathbb{A}_{\S}^{-}\;\;\;=\;\;\;\frac{ \s }{ 2 ω } \; \cdot \; ω } \] | (SN.Ei.S.G.6) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\# \mathbb{A}_{\S}^{-}\;\;\;=\;\;\;\frac{ \s }{ 2 } } \] | (SN.Ei.S.G.7) |
Dies passt dann eben auch zu Formel .
So ergibt sich dann schlüssig mit Formel :
Es gibt also eine quasi Spiegelung der Anzahlen von positiven und negativen ganzen Zahlen.
Aber die Spiegelung der Werte der ganzen Zahlen an der Null ist nicht korrekt. Die Spiegelung der Werte findet beim Wert $ -½ $ statt (siehe ). Wir sehen, es kann der falsche Eindruck einer Spiegelung der Entitäten der ganzen Zahlen oder der reell algebraischen Zahlen entstehen, wenn wir die Intervalle zwischen den ganzen Zahlen nicht explizit berücksichtigen und durch Dranhängen visualisieren würden.
Demnach sind wir sicher, dass die Anzahl der endlichen ganzen Zahlen wirklich $ 2 ω $ ist.
Die superiale Basis $ \s $ hat bezüglich der Struktur des Aktual-Unendlichen eine bemerkenswerte doppelte Bedeutung
Bezüglich der Anzahl von Zahlen in Mengen kommt die superiale Basis $ \s $ in zwei sehr ähnlichen und doch ganz unterschiedlichen Zusammenhängen vor, die in der Gegenüberstellung aufhorchen lassen und nachdenklich machen können. Eine bemerkenswerte Doppelung, wie ich finde, wo die eine Seite schließlich perfekt in die andere Seite greift.
Eine bemerkenswerte Doppelung
Formel zeigt uns mit $ \# \mathbb{A}_{\S} = \s $,
dass die Menge aller sinnvollen Koeffizienten der Superial-Zahlen die gleiche Anzahl an Elementen enthalten muss,
wie die Menge der superial kleinen ganzen Zahlen von der Null bis ohne die Eins $ \# \left( \lbrack 0, 1 \lbrack_{\mathbb{S}_{\N}^{-1}} \right) = \s $.
Die superial kleinen ganzen Zahlen und diese Formel ihrer Anzahl ergeben sich aus der arithmetischen Struktur der Geometrie
durch die Erkenntnis, dass die Teilung der Strecke zwischen Null und Eins in $ \s $ Teile zu $ \s $ Teilstrecken der Länge $ \s^{-1} $ führen muss.
Interessant ist im Vergleich, dass in der Menge $ \mathbb{A}_{\S} $ nur endliche Werte existieren, während in der Menge $ \lbrack 0, 1 \lbrack_{\mathbb{S}_{\N}^{-1}} $ die weit überwiegende Mehrheit der Elemente aktual unendlich kleine Summanden beinhaltet. Denn bei der Teilung der Strecke zwischen Null und Eins entsteht dadurch die Menge $ \lbrack 0, 1 \lbrack_{\mathbb{S}_{\N}^{-1}} $ der Punkte zwischen den Teilstrecken, die Adressierbar sind und deren benachbarte Punkte jeweils den Abstand beziehungsweise die Differenz $ \s^{-1} $ haben, was nur mit aktual unendlich kleinen Summand dieser Differenz beschreibbar ist.
Es ist, als wenn in der Geometrie die Anzahl $ \s $ an Entitäten – Existenzen – im endlichen auf einer endlosen Geraden, die den Zahlen der Menge $ \mathbb{A}_{\S} $ entsprechen, nicht dichter gepackt werden kann. Bei dem Versucht, die gleiche Anzahl an Entitäten auf kleinerem Raum – also dichter oder enger – zu packen, so, wie dies bei $ \lbrack 0, 1 \lbrack_{\mathbb{S}_{\N}^{-1}} $ geschieht, müssen folglich Anteile aktual unendlich kleiner Summanden herausfallen. Diese aktual unendlich kleinen Summanden, sind ganze Zahlen im superial Kleinen.
Die Zahlen der Menge $ \mathbb{A}_{\S} $, können – zumindest im Rahmen der Superial-Zahlen – als die maximal dichten Zahlen unserer endlichen Zahlengeraden verstanden werden. also als die Grundlage unserer Geometrie im Endlichen.
Die superial kleinen ganzen Zahlen der Menge $ \lbrack 0, 1 \lbrack_{\mathbb{S}_{\N}^{-1}} $ und deren Erweiterung auf den ganzen Zahlenstrahl, spielen dann eine zentrale Rolle in der neuen Differenzialrechnung auf Basis von Superial-Zahlen. Das tun sie zum einen in den Differenzen der Ableitung und sodann auch, zum anderen, bei der Integration, wo die superial kleinen ganzen Zahlen als Indizes der Summenglieder auftreten.
Existenz der maximalen Dichte der Zahlengeraden
Die eben entwickelte Vorstellung, dass eine weitere Verdichtung der maximaldichten rein endlichen Zahlengeraden zum „herausfallen“ aktual unendlich kleiner ganzer Summanden führt,
passt, wie oben gesagt, genau zu unserer Feststellung auf der Seite ›Die arithmetische Struktur der Geometrie‹.
Dort teilen wir die Strecke von der Null bis zur Eins mit Hilfe unserer endlichen Primzahlen jeweils bis zur Potenz der vollständigen Induktion $ ω $. Wobei wir feststellen, dass wir diese Strecke nicht sinnvoll noch feiner mit Hilfe endlicher Primzahlen teilen können, weil wir so bereits am Beginn einer aktual unendlichen fraktalen Wiederholung der arithmetischen Struktur der Geometrie angekommen sind.
So erkennen wir dann auch durch den Beweis der Überrationalitätsvermutung, dass wir mit dem Primzahl-Flächenprodukt $ \s $, der $ ω $-ten Potenz aller endlichen Primzahlen, bei der Teilung durch $ \s $ eine Feinheit der Teile erreichen, die nachweislich auch alle durch Radikale darstellbaren reell algebraischen Zahlen umfasst, also auch die irrationalen Wurzeln, wie beispielsweise $ \sqrt{ 2 } $, $ \sqrt{ 5 } $ oder den Goldenen Schnitt $ φ = \frac{ \sqrt{ 5 } + 1 }{ 2 } $, wenn nicht sogar alle reell algebraischen Zahlen.
Dies könnte in meinen Augen eben auch „mathematisch perfekt“ zur ›Algebraische-Koeffizienten-Vermutung‹ und zur ›Superiale-Transzendenz-Vermutung‹ passen, die ja beide noch zu beweisen sind. Es passte deshalb sehr gut, weil hinter diesen Vermutungen steht, dass die Trennlinie zwischen den Fraktalebenen der Superial-Zahlen im Grunde auch der Trennlinie zwischen den reell algebraischen Zahlen und den transzendenten Zahlen entspricht. Das würde also gut die bekannte Aufteilung der Zahlenmengen und deren Trennung ontologisch klar und verständlich erklären.
Und auch die Einblicke in die Zusammenhänge zwischen ganzen und reell algebraischen Zahlen vertieften sich deutlich und klar.
Tiefer Zusammenhang zwischen den Primzahlen und den sinnvollen Koeffizienten der Superial-Zahlen
Möglicherweise sogar zwischen den Primzahlen und den reell algebraischen Zahlen
Entspricht die Menge $ \mathbb{A}_{\S} $ tatsächlich der Menge aller reell algebraischen Zahlen $ \mathbb{A}_{\R} $,
dann werden diese in eine sehr enge existenzielle Beziehung mit den endlichen Primzahlen gebracht, die ich bisher so noch nicht gesehen habe
und die Anlass zu der Annahme gibt, dass wir diese in Zukunft noch detaillierter formulieren können.
Klar ist schon, dass das Raster des Primzahl-Flächenproduktes von $ \s $ aufs engste mit den sinnvollen Koeffizienten der Superial-Zahlen $ \mathbb{A}_{\S} $ – und, wenn $ \mathbb{A}_{\S} \overset{?}{=} \mathbb{A}_{\R} $, mit den reell algebraischen Zahlen $ \mathbb{A}_{\R} $ – verwoben ist. Denn alle $ a \cdot \s $, mit $ a \in \mathbb{A}_{\S} $, müssen nach Formel SN.SinK.2 ganze Zahl sein, siehe sinnvolle Koeffizienten der Superial-Zahlen. Dies ist ein fundamentaler Zusammenhang, der weitere Erkenntnisse erwarten lässt.
Der Beweis der Überrationalitätsvermutung zeigt beispielsweise für $ a = \sqrt{2} = \frac{ \sqrt{2} \cdot 2^{ω} }{ 2^{ω} } = \frac{ 2^{\frac{1}{2}} \cdot 2^{ω} }{ 2^{ω} } = \frac{ 2^{ω + \frac{1}{2}} }{ 2^{ω} } $, anhand dieses ganzzahligen Bruchs, dass $ \sqrt{2} \cdot \s $ eine ganze Zahl ist. Und zwar, weil $ \sqrt{2} \cdot 2^{ω} $ eine ganze Zahl ist, ebenso wie $ \s $, dessen Primzahl-Flächenprodukt ja auch den Faktor $ 2^{ω} $ enthält. Deshalb ist $ \sqrt{2} $ ein sinnvoller Koeffizient und es gilt $ \sqrt{2} \in \mathbb{A}_{\S} $. Schon hierin liegen einige erstaunliche neue Erkenntnisse, die bisher offenbar unbekannt waren. Denn wir lernen beim Beweis der Überrationalitätsvermutung zum Beispiel, wie wir irrationale Wurzeln durch Brüche mit aktual unendlichen Quotienten, von mir überrationale Brüche genannt, darstellen können. Und wir lernen, auch, wenn das Kürzen eines überrationalen Bruchs möglich ist, kann es dazu führen, dass wir eine gesuchte Lösung nicht finden können, wenn wir es tun.
Die Ähnlichkeit beider Mengen
Die Mengen werden beide mit sehr ähnlichen Definitionen beschrieben, an denen wir auch recht schnell erkennen können,
dass sie tatsächlich die gleiche Anzahl an Elementen beinhalten müssen:
Diese Menge in ihrer Normalform, nur mit endlichen natürlichen Zahlen bis ohne $ \s $, also bis ins aktual unendlich Große, gezählt, sieht dann so aus, nur zur Verdeutlichung:
| ▾ | In Stellenwert-Notation: |
Diese Menge in ihrer Normalform, nur mit endlichen natürlichen Zahlen bis ohne $ \s $, also bis ins aktual unendlich Große, gezählt, sieht dann so aus, nur zur Verdeutlichung:
Wobei die Elemente der Mengen dann konkret in Ausschnitten folgendermaßen aussehen, wenn $ φ $ der Goldene Schnitt ist:
Diese Menge in ihrer Normalform, nur mit endlichen natürlichen Zahlen bis ohne $ \s $, also bis ins aktual unendlich Große, gezählt, sieht dann so aus, nur zur Verdeutlichung:
| ▾ | In Stellenwert-Notation: |
Diese Menge in ihrer Normalform, nur mit endlichen natürlichen Zahlen bis ohne $ \s $, also bis ins aktual unendlich Große, gezählt, sieht dann so aus, nur zur Verdeutlichung:
Auffällig ist, dass bei der Menge $ \lbrack 0, 1 \lbrack_{\mathbb{S}_{\N}^{-1}} $ zu Beginn und am Ende die ganzen Zahlen $ \mathbb{Z} $ in $ \mathbb{N} $ und $ \mathbb{Z}^{-} $ aufgespalten sind und mitten drinne ganz $ \mathbb{Z} $ unendlich oft durchläuft, jedoch $ \lbrack 0, 1 \lbrack_{\mathbb{A}_{\S}} $ nur ein Mal durchlaufen wird.
Während die ganzen Zahlen $ \mathbb{Z} $ bei $ \mathbb{A}_{\S} $ nur ein Mal komplett durchlaufen werden. Die Menge $ \lbrack 0, 1 \lbrack_{\mathbb{A}_{\S}} $ wird jedoch unendlich oft durchlaufen.
Wenn nun aber beide Mengen die gleiche Anzahl an Elementen, sprich Zahlen, haben, dann stellt sich die Frage, ob und wie wir die Mengen aufeinander abbilden können.
Die Bedeutung beider Mengen im Stellenwertsystem der Superial-Zahlen
Die Menge $ \mathbb{A}_{\S} $ steht im Stellenwertsystem
der Superial-Zahlen für alle sinnvollen Koeffizienten,
dann entspricht die Anzahl ihrer Elemente quasi der Anzahl der möglichen Ziffern, nämlich $ \s $.
Da macht es natürlich Sinn, dass es genau so viele Ziffern gibt, wie die Basis des Stellenwertsystems, also ebenfalls $ \s $.
Dies ist bei anderen Stellenwertsystemen ebenso.
Beispielsweise gibt es im Zehnersystem genau zehn Ziffern.
Allerdings sind in der Menge $ \mathbb{A}_{\S} $ nicht nur natürliche Zahlen, wie bei den „gewöhnlichen“ Stellenwertsystemen,
sondern die meisten sind gebrochen und es sind sogar auch die negativen dabei.
Gleichzeitig ist die Menge $ \lbrack 0, 1 \lbrack_{\mathbb{S}_{\N}^{-1}} $ in ihrer Normalform $ \lbrack 0, \s \lbrack_{\mathbb{S}_{\N}} $ die Grundlage des Zählens von $ \s $ vielen, auch aktual unendlichen natürlichen Zahlen von Null bis ohne $ \s $. Dies entspricht in gewisser Weise ganzen Ziffern des Stellenwertsystems der Superial-Zahlen. Allerdings sind diese natürlichen Superial-Zahlen nicht die Koeffizienten des Stellenwertsystemens, wie wir es beispielsweise aus dem Zehnersystem für die ersten zehn Ziffern kennen. Dies kommt, weil bei den natürlichen Superial-Zahlen keine reinen Ziffern, sondern beim Übergang ins Aktual-Unendliche selber schon gemischte Zahlen im Sinne des Stellenwertsystems, wie beispielsweise $ \left\langle ⅔ \right\rangle \left\langle 7 \right\rangle\!. = ⅔ \s + 7 $, auftreten.
Die absolute Außergewöhnlichkeit des Stellenwertsystems der Superial-Zahlen
Die sinnvollen Koeffizienten und das natürliche Zählen fallen bei den Superial-Zahlen auseinander und passen gleichzeitig so auch perfekt ineinander.
Es erscheint ein wenig wie ein Wunder, dass beides exakt einander entspricht, ja entsprechen muss.
Diese Zwittrigkeit oder Zwitternatur der Anzahl $ \s $ in den ihr entsprechenden wichtigen Mengen unseres neuen Stellenwertsystemens, welche keine Widersprüchlichkeit ist, sondern in sich vollständig plausibel, machen es so außergewöhnlich. Dadurch bekommt es die Eigenschaften, die wir für die Beschreibung der Geometrie brauchen, um schließlich auch Differenzialrechnung darin zu betreiben.
Fragen die bleiben sind:
| • |
Können wir noch besser verstehen, warum das so ist oder sein muss? |
| • |
Hat diese Doppelung eventuell eine Verbindung zur analytischen Fortsetzung von Funktionen und damit zur Riemannschen Vermutung? |
| ▾ | Experimentell: Sind beide Mengen aufeinander linear abbildbar? |
Naiv können wir einmal annehmen, da die Werte beider Mengen offenbar nicht nur wohlgeordnet sind, sondern auch alle je in ihrer Menge die gleichen Abstände untereinander haben, dass sie vielleicht rein durch Verschiebung und einen Faktor Element für Element ihrer Reihenfolge nach aufeinander abgebildet werden können. Weil der Wertebereich von $ \mathbb{A}_{\S} $ nun $ 2 ω $ mal so groß ist, wie der von $ \lbrack 0, 1 \lbrack_{\mathbb{S}_{\N}^{-1}} $, und um die Mitte zentriert, womit wir als Ansatz eine Verschiebung um $ - ½ $ annehmen:
Betrachten wir als erstes die Grenzbereiche dieser versuchten Mengendefinition. Die linksseitige Grenze ist in der Menge $ \lbrack 0, 1 \lbrack_{\mathbb{S}_{\N}^{-1}} $ die Null und wird durch den neuen Definitionsversuch zu:
Hier sehen wir, dass die linksseitige Grenze Null zu $ - ω $ wird, was aber kein Element von $ \mathbb{A}_{\S} $ ist.
Die rechtsseitige Grenze $ 1 - \s^{-1} $ wird zu:
Die rechtsseitige Grenze $ 1 - \s^{-1} $ wird zu $ ω - 2 ω \s^{-1} $, was auch kein Element von $ \mathbb{A}_{\S} $ ist. Beide Grenzen werden zu aktual unendlich großen Werten, aber $ \mathbb{A}_{\S} $ enthält nur endliche Werte.
Was wird aus dem mittleren Wert? Was ist der mittlere Wert? Wir nehmen mal an, es ist $ ½ $:
Der mittlere Wert $ ½ $ wird zu Null. Doch Null ist vermutlich nicht der mittlere Wert von $ \mathbb{A}_{\S} $, denn der Mittelpunkt von $ \# \mathbb{Z} $ ist $ - ½ $.
(In Arbeit …)
Das Problem scheint …
Gleich mächtig, aber nur bedingt abbildbar …
Die Elemente beider Mengen sind nicht nach ihrer Größe geordnet aufeinander abbildbar, sondern nur,
wenn wir ihre Reihenfolge verändern ???
(In Arbeit …)
Die superiale Basis $ \s $ und die Ordinalzahl $ ω^{ω} $ im Strukturvergleich
Vom Wert her gleich und doch verschieden
Betrachten wir die arithmetische Struktur der Geometrie $ \s $ und die Adressierbarkeit ihrer Punkte, die durch die Teilung durch $ \s $ entstehen, dann ist es interessant, dass wir durch den Beweis der Primzahlprodukt-Vermutung auch in den Ordinalzahlen eine Wertgleichheit zu $ \s $ finden:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \s\;\;\;=\;\;\;ω^{ω} } \] | (SN.PP.174) |
In der echten Klasse der Ordinalzahlen $ \mathbb{On} $ hat das Element $ ω^{ω} $ genau so viele Vorgänger, wie sein Wert groß ist, nämlich die Elemente $ \left\lbrack 0, ω^{ω} \right\lbrack_{\mathbb{On}} $. Dies gilt ebenso für das Element $ \s $ in der Menge der natürlichen Superial-Zahlen $ \mathbb{S_{\N}} $, wo $ \left\lbrack 0, \s \right\lbrack_{\mathbb{S}_{\N}} $ alle Vorgänger enthält. Die Gleichheit der Werte drückt folglich aus, dass in beiden Fällen gleich viele Vorgänger vorhanden sind, die Vorgängermengen also gleich viele Elemente haben.
Für alle Elemente in $ \mathbb{On} $ und in $ \mathbb{S_{\N}} $ gilt, dass jedes Element genau so viele Vorgänger hat, wie sein Wert ausdrückt, womit beide zur Klasse $ \mathbb{K}_{\infty,c} $ der Anzahl äquivalenten Klassen gehören:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \mathbb{On}\;\;\;\in\;\;\;\mathbb{K}_{\infty,c} } \] | (BO.Ein.NE.79) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \mathbb{S}_{\N}\;\;\;\in\;\;\;\mathbb{K}_{\infty,c} } \] | (SN.Ei.S.V.1) |
In beiden Klassen $ \mathbb{On} $ und $ \mathbb{S_{\N}} $ – denn eine Menge ist nur eine besondere Klasse – haben auch alle Zahlen einen direkten Nachfolger. Und trotzdem sind beide von ihren Elementen her nicht gleich, denn in $ \mathbb{S_{\N}} $ haben alle Zahlen auch einen direkten Vorgänger, außer die Null. In $ \mathbb{On} $ hingegen gilt dies nicht, weil nicht nur die Null keinen direkten Vorgänger hat, sondern alle sogenannten Limeszahlen haben keinen direkten Vorgänger. Also haben $ ω $ und $ ω^{ω} $ ebenfalls keine direkten Vorgänger:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}[ 0, \s [_{\mathbb{S}_{\N}}\;\;\;\neq\;\;\;[ 0, ω^{ω} [_{\mathbb{On}} } \] | (SN.Ei.S.V.2) |
Der strukturelle Unterschied dieser beiden Anzahl äquivalenten Klassen – beim Vergleich werden die Werte betrachtet –, trotz Wertgleichheit von $ \s $ und $ ω^{ω} $, ist sehr bemerkenswert und bedarf einer näheren Untersuchung.
Die beiden Mengen sehen konkret folgendermaßen aus:
Wir sehen: In der Menge $ \left\lbrack 0, \s \right\lbrack_{\mathbb{S}_{\N}} $ sind Elemente der Menge $ \left\lbrack 0, ω^{ω} \right\lbrack_{\mathbb{On}} $, wie $ ω $, $ ω + 1 $ oder $ ω^{2} $, $ ω^{2} + 1 $ und so weiter, gar nicht enthalten. Umgekehrt gibt es in $ \left\lbrack 0, ω^{ω} \right\lbrack_{\mathbb{On}} $ keinen direkten Vorgänger von $ ω^{ω} $, wie es sie in der Menge der natürlichen Superial-Zahlen vor $ \s $ mit $ \s - 1 $ und so weiter gibt. Und auch Ausdrücke, wie $ \frac{1}{2} \s $ oder $ \frac{\sqrt{5}}{3} \s + 1 $ können wir in $ \left\lbrack 0, ω^{ω} \right\lbrack_{\mathbb{On}} $ nicht finden und benennen.
Genauer können wir sagen, außer allen natürlichen Zahlen gibt es keine einzige weitere Zahl, die wir in beiden Mengen explizit angeben können. Aber die Anzahl aller Zahlen, wie gesagt, und sogar ihre Summe, wie wir gleich sehen werden, sind in beiden Mengen gleich.
Summengleichheit trotz der strukturellen Unterschiede
Mit der angepassten Gaußschen Summenformel, damit auch die Berechnung von Summen unendlich großer Mengen, die kein größtes Element haben, möglich ist, können wir die Summen ganzer Zahlen von Null bis ohne $ \s $ oder $ ω^{ω} $ berechnen, wenn die Klassen ihrer Vorgänger zur Klasse $ \mathbb{K}_{\infty,g} $ Gauß-Summen äquivalenter Klassen gehören:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \left( \mathbb{M} \in \mathbb{K}_{\infty,g} \right) \left( \forall n \in \mathbb{M} \right) \left[\; \sum_{ \forall i \in [ 0, n [_{\mathbb{M}} } \!\!\!\! i\;\;\;=\;\;\;\frac{ n^{2} - n }{ 2 } \;\right] } \] | (BO.Ein.NE.82) |
Für die Summe aller endlichen natürlichen Zahlen erhalten wir beispielsweise:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \sum_{ \forall i \in ω } i\;\;\;=\;\;\;\frac{ ω^{2} - ω }{ 2 } } \] | (BO.Ein.NE.85) |
Für die beiden gleichwertigen Zahlen und die Summen der unendlich vielen positiven ganzen Zahlen, für die sie jeweils stehen, erhalten wir dann:
Die Richtigkeit der Summe aller natürlichen Superial-Zahlen bis ohne $ \s $ besteht schon wegen Formel BO.Ein.NE.83 aufgrund der Tatsache, dass diese Menge zur Klasse $ \mathbb{K}_{\infty,c} $ der Anzahläquivalenten Klassen gehört:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}\mathbb{S}_{\N}\;\;\;\in\;\;\;\mathbb{K}_{\infty,g} } \] | (SN.Ei.S.V.7) |
So gehört sie dann auch zur Klasse $ \mathbb{K}_{\infty,g} $ der Gauß-Summen äquivalenten Klassen.
Desweiteren sehen wir diese Richtigkeit noch an zwei Dingen zusammen. Zum einen an dem allgemeinen Beweis, dass das Ableitung die Umkehrung des Integrals ist. Und zum anderen an dem Beispiel der Integration der Ableitung von $ f(x) = x^{2} $, also von $ f'(x) = \left\langle 2 x \right\rangle\!. \left\langle 1 \right\rangle $, in dem genau die angepasste Gaußsche Summenformel zur korrekten Lösung angewandt wird und der einzige fragliche Term ist.
Die Richtigkeit der Summe aller Ordinalzahlen bis ohne $ ω^{ω} $ ist bereits aus Formel BO.Ein.NE.84 bekannt und ergibt sich ganz einfach aus der Definition der Ordinalzahlen, die dazu gemacht sind, solche Zusammenhänge über die vollständige Induktion der natürlichen Zahlen auszudrücken. Nur, dass der Wert ohne die Biordinalzahlen bisher nicht ausgedrückt werden konnte, was nun möglich ist.
Aus der Wertgleichheit beider Werte in der Formel SN.PP.174 folgt dann
und dies, obwohl die Mengen, deren Elemente hier summiert werden, ja recht unterschiedlich sind. Und genau hier kann die nähere Untersuchung interessant sein.
Wenn wir die Menge $ \left\lbrack 0, \s \right\lbrack_{\mathbb{S}_{\N}} $ aller natürlichen Superial-Zahlen bis ohne $ \s $ mit $ ω^{ω} $ ausdrücken, dann erhalten wir:
Vergleichen wir ihre Elemente nun mit denen der davor stehenden Menge $ \left\lbrack 0, ω^{ω} \right\lbrack_{\mathbb{On}} $ in Formel so fällt auf, dass die aktual unendlich großen Elemente der Menge hier mit endlichen Faktoren vor $ ω^{ω} $ ausgedrückt werden, also quasi im Bereich von $ ω^{ω} $, während die genannte Menge $ \left\lbrack 0, ω^{ω} \right\lbrack_{\mathbb{On}} $ oben nur Elemente weiter unterhalb von $ ω^{ω} $ enthält, ohne $ ω^{ω} $ selbst in den Ausdrücken zu benutzen.
Umso erstaunlicher, dass beide Mengen nicht nur gleich viele Elemente, sondern auch die gleiche Summe haben, wie vorstehend gezeigt. Es stellt sich demnach so dar, dass beide Mengen trotz ihrer Unterschiede in gewisser Hinsicht äquivalent sind. Die endlichen Faktoren vor $ ω^{ω} $ beziehungsweise $ \s $ werden also in ihrer potenziellen Unendlichkeit doch sehr klein, während die Polynome des Wertes $ ω $ potenziell doch sehr groß werden.
Wie oben bereits geklärt dürfen wir zur Berechnung der Summe die angepasste Gaußsche Summenformel einsetzen. Insofern ist die folgende Berechnung nicht der Beweis dafür, dass diese Summe innerhalb der natürlichen Superial-Zahlen korrekt ist, denn das wissen wir schon. Sondern es ist die Probe, dass sich auch wirklich das oben gezeigte Ergebnis aus dem von uns bereits entwickelten Wissen ergibt, wenn wir die Summe in allen Einzelheiten berechnen. Es ist also unser Plausibilitäts-Check.
Wenn wir die Elemente der Menge $ \left\lbrack 0, \s \right\lbrack_{\mathbb{S}_{\N}} $
summieren, ergibt sich nach der angepassten Gaußschen Summenformel
für die erste Zeile, die alle endlichen natürlichen Zahlen enthält, die Summe:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \sum_{ \forall i \in \mathbb{N} } i\;\;\;=\;\;\;\sum_{ \forall i \in ω } i\;\;\;=\;\;\;\frac{ ω^{2} - ω }{ 2 } } \] | (BO.Ein.NE.85) |
Um die mittleren Zeilen der Gesamtsumme, ohne die erste und die letzte, zu berechnen, benötigen wir folgende Formeln:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \# \mathbb{Z}^{-}\;\;\;=\;\;\;\# \mathbb{N}\;\;\;=\;\;\;ω\;\;\;=\;\;\;\mathbb{N} } \] | (BO.Ein.NE.6) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \# \mathbb{Z}\;\;\;=\;\;\;2 ω } \] | (BO.Ein.NE.7) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \sum_{ \forall z \in \mathbb{Z}} z\;\;\;=\;\;\;- ω } \] | (BO.Ein.NE.12) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\sum_{ \forall z \in \mathbb{Z}} z\;\;\;=\;\;\;\sum_{ \forall z^{-} \in \mathbb{Z}^{-} } \!\! z^{-} + \sum_{ \forall n \in \mathbb{N} } n } \] | (SN.Ei.S.V.10) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}- ω\;\;\;=\;\;\;\sum_{ \forall z^{-} \in \mathbb{Z}^{-} } \!\! z^{-} + \frac{ ω^{2} - ω }{ 2 } } \] | (SN.Ei.S.V.11) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\sum_{ \forall z^{-} \in \mathbb{Z}^{-} } \!\! z^{-}\;\;\;=\;\;\;- \frac{ ω^{2} - ω }{ 2 } - ω } \] | (SN.Ei.S.V.12) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \# \left( [ 0, 1 [_{\mathbb{A}_{\S}} \right)\;\;\;=\;\;\;\frac{ \s }{ 2 ω } } \] | () | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\# ] 0, 1 [_{\mathbb{A}_{\S}}\;\;\;=\;\;\;\frac{ \s }{ 2 ω } - 1 } \] | (SN.Ei.S.V.13) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \sum_{ \forall a \in [ 0, x [_{\mathbb{A}_{\S}}} \!\! a\;\;\;=\;\;\;\frac{ x^{2} \cdot \s }{ 4 ω } - \frac{ x }{ 2 } } \] | (SN.AbIn.NU.39) | ||
Für die mittleren Zeilen ergibt sich dann, wenn wir die Summe mit $ y $ zur Übersichtlichkeit substituieren:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \sum_{ \forall a \in ] 0, 1 [_{\mathbb{A}_{\S}} } \sum_{ \forall z \in \mathbb{Z} } \left( a \cdot ω^{ω} + z \right)\;\;\;=\;\;\;y } \] | (SN.Ei.S.V.14) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}y\;\;\;=\;\;\;\sum_{ \forall a \in ] 0, 1 [_{\mathbb{A}_{\S}} } \left( a \cdot ω^{ω} \cdot \# \mathbb{Z} + \! \sum_{ \forall z \in \mathbb{Z} } z \right) } \] | (SN.Ei.S.V.15) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}y\;\;\;=\;\;\;\sum_{ \forall a \in ] 0, 1 [_{\mathbb{A}_{\S}} } \left( a \cdot ω^{ω} \cdot 2 ω + \! \sum_{ \forall z \in \mathbb{Z} } z \right) } \] | (SN.Ei.S.V.16) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}y\;\;\;=\;\;\;\sum_{ \forall a \in ] 0, 1 [_{\mathbb{A}_{\S}} } \!\!\!\! \left( a \cdot ω^{ω} \cdot 2 ω + \left( - ω \right) \right) } \] | (SN.Ei.S.V.17) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}y\;\;\;=\;\;\;\sum_{ \forall a \in ] 0, 1 [_{\mathbb{A}_{\S}} } \!\!\!\! \left( a \cdot ω^{ω} \cdot 2 ω - ω \right) } \] | (SN.Ei.S.V.18) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}y\;\;\;=\;\;\;\sum_{ \forall a \in ] 0, 1 [_{\mathbb{A}_{\S}} } \!\!\!\! a \cdot ω^{ω} \cdot 2 ω \;\; - \!\! \sum_{ \forall a \in ] 0, 1 [_{\mathbb{A}_{\S}} } \!\!\!\! ω } \] | (SN.Ei.S.V.19) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}y\;\;\;=\;\;\;ω^{ω} \cdot 2 ω \cdot \!\! \sum_{ \forall a \in ] 0, 1 [_{\mathbb{A}_{\S}} } \!\!\!\! a \;\; - \!\! \sum_{ \forall a \in ] 0, 1 [_{\mathbb{A}_{\S}} } \!\!\!\! ω } \] | (SN.Ei.S.V.20) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}y\;\;\;=\;\;\;ω^{ω} \cdot 2 ω \cdot \!\! \sum_{ \forall a \in ] 0, 1 [_{\mathbb{A}_{\S}} } \!\!\!\! a \;\; - \;\; \left( \frac{ \s }{ 2 ω } - 1 \right) \cdot ω } \] | (SN.Ei.S.V.21) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}y\;\;\;=\;\;\;ω^{ω} \cdot 2 ω \cdot \!\! \sum_{ \forall a \in ] 0, 1 [_{\mathbb{A}_{\S}} } \!\!\!\! a \;\; - \;\; \left( \frac{ ω^{ω} }{ 2 ω } - 1 \right) \cdot ω } \] | (SN.Ei.S.V.22) | ||
Um die noch enthaltene variable Summe zu berechnen, können wir, ohne sie zu verändern, die Null in ihre Basismenge integrieren und sie dann mit Hilfe von Formel SN.AbIn.NU.39 berechnen:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}y\;\;\;=\;\;\;ω^{ω} \cdot 2 ω \cdot \!\! \sum_{ \forall a \in [ 0, 1 [_{\mathbb{A}_{\S}} } \!\!\!\! a \;\; - \;\; \left( \frac{ ω^{ω} }{ 2 ω } - 1 \right) \cdot ω } \] | (SN.Ei.S.V.23) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}y\;\;\;=\;\;\;ω^{ω} \cdot 2 ω \cdot \!\! \sum_{ \forall a \in [ 0, 1 [_{\mathbb{A}_{\S}} } \!\!\!\! a \;\; - \;\; \left( \frac{ ω^{ω} \cdot ω }{ 2 ω } - ω \right) } \] | (SN.Ei.S.V.24) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}y\;\;\;=\;\;\;ω^{ω} \cdot 2 ω \cdot \!\! \sum_{ \forall a \in [ 0, 1 [_{\mathbb{A}_{\S}} } \!\!\!\! a \;\; - \;\; \left( \frac{ ω^{ω} }{ 2 } - ω \right) } \] | (SN.Ei.S.V.25) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}y\;\;\;=\;\;\;ω^{ω} \cdot 2 ω \cdot \!\! \sum_{ \forall a \in [ 0, 1 [_{\mathbb{A}_{\S}} } \!\!\!\! a \;\; - \;\; \frac{ ω^{ω} }{ 2 } \;\; + \;\; ω } \] | (SN.Ei.S.V.26) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}y\;\;\;=\;\;\;ω^{ω} \cdot 2 ω \cdot \left( \frac{ \s }{ 4 ω } - \frac{ 1 }{ 2 } \right) \;\; - \;\; \frac{ ω^{ω} }{ 2 } \;\; + \;\; ω } \] | (SN.Ei.S.V.27) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}y\;\;\;=\;\;\;ω^{ω} \cdot 2 ω \cdot \left( \frac{ ω^{ω} }{ 4 ω } - \frac{ 1 }{ 2 } \right) \;\; - \;\; \frac{ ω^{ω} }{ 2 } \;\; + \;\; ω } \] | (SN.Ei.S.V.28) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}y\;\;\;=\;\;\;\frac{ ω^{ω} \cdot 2 ω \cdot ω^{ω} }{ 4 ω } - \frac{ ω^{ω} \cdot 2 ω }{ 2 } - \frac{ ω^{ω} }{ 2 } + ω } \] | (SN.Ei.S.V.29) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}y\;\;\;=\;\;\;\frac{ \left( ω^{ω} \right)^{2} }{ 2 } - ω^{ω} \cdot ω - \frac{ ω^{ω} }{ 2 } + ω } \] | (SN.Ei.S.V.30) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}y\;\;\;=\;\;\;\frac{ \left( ω^{ω} \right)^{2} - ω^{ω} }{ 2 } - ω^{ω} \cdot ω + ω } \] | (SN.Ei.S.V.31) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}y\;\;\;=\;\;\;\frac{ \left( ω^{ω} \right)^{2} - ω^{ω} }{ 2 } - \left( ω^{ω} \cdot ω - ω \right) } \] | (SN.Ei.S.V.32) | ||
Die letzte Zeile summiert sich dann zu:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \sum_{ \forall z^{-} \in \mathbb{Z}^{-} } \left( ω^{ω} + z^{-} \right)\;\;\;=\;\;\;\sum_{ \forall z^{-} \in \mathbb{Z}^{-} } ω^{ω} \; + \! \sum_{ \forall z^{-} \in \mathbb{Z}^{-} } \!\! z^{-} } \] | (SN.Ei.S.V.33) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\!\! \sum_{ \forall z^{-} \in \mathbb{Z}^{-} } \left( ω^{ω} + z^{-} \right)\;\;\;=\;\;\;ω^{ω} \cdot ω \; + \! \sum_{ \forall z^{-} \in \mathbb{Z}^{-} } \!\! z^{-} } \] | (SN.Ei.S.V.34) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\!\! \sum_{ \forall z^{-} \in \mathbb{Z}^{-} } \left( ω^{ω} + z^{-} \right)\;\;\;=\;\;\;ω^{ω} \cdot ω + \left( - \frac{ ω^{2} - ω }{ 2 } - ω \right) } \] | (SN.Ei.S.V.35) | ||
Wenn wir alle drei Summen nun addieren
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \sum_{ \forall i \in [ 0, \s [_{\mathbb{S}_{\N}} } \!\!\! i\;\;\;=\;\;\;\frac{ ω^{2} - ω }{ 2 } \\ \qquad\qquad\quad\;\; + \frac{ \left( ω^{ω} \right)^{2} - ω^{ω} }{ 2 } - \left( ω^{ω} \cdot ω - ω \right) \\ \qquad\qquad\quad\;\; + ω^{ω} \cdot ω + \! \left( - \frac{ ω^{2} - ω }{ 2 } - ω \right) } \] | (SN.Ei.S.V.36) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\!\! \sum_{ \forall i \in [ 0, \s [_{\mathbb{S}_{\N}} } \!\!\! i\;\;\;=\;\;\;\frac{ \left( ω^{ω} \right)^{2} - ω^{ω} }{ 2 } - ω^{ω} \cdot ω + ω \\ \qquad\qquad\qquad\qquad\;\; + ω^{ω} \cdot ω - ω } \] | (SN.Ei.S.V.37) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\!\! \sum_{ \forall i \in [ 0, \s [_{\mathbb{S}_{\N}} } \!\!\! i\;\;\;=\;\;\;\frac{ \left( ω^{ω} \right)^{2} - ω^{ω} }{ 2 } } \] | (SN.Ei.S.V.38) | ||
ergibt sich auch tatsächlich das erwartete Ergebnis.
Unser Plausibilitäts-Check ist also positiv ausgefallen.
Die Wertgleichheit von $ \s $ und $ ω^{ω} $ sowie die Gleichheit der Summe ihrer natürlichen Vorgänger markiert die besondere Bedeutung ihres Werts
| ▾ | Notizen |
• Mein Gefühl sagt mir, dass die Wertgleichheit von $ \s $ und $ ω^{ω} $ und deren unterschiedliche Zählstruktur etwas mit dem Zusammenhang zwischen den Nullstellen von Polynomen und deren Lösungen in Form von algebraischen Zahlen zu tun hat.
• Wir können auch sagen, dass die Superial-Zahlen eher mit den $ ω $-ten Potenzen von Primzahlen oder natürlichen Zahlen in Verbindung stehen, während die Ordinalzahlen mit der Basis $ ω $ in natürlichen Potenzen im Zusammenhang stehen. Bei $ ω^{ω} $ treffen sich beide Perspektiven dann.
Das der Wert der aktual unendlichen geometrischen Teilung der Eins $ \s $ mit dem Wert der aktual unendlich möglichen Varianten an Polynomen $ ω^{ω} $ zusammenfällt, drückt seine besondere Bedeutung aus.
Es handelt sich nicht um irgendeinen Wert, sondern darum, wie oft wir die endlich lange Strecke von der Null bis zur Eins normiert teilen können, ohne zur Beschreibung der Teilungspunkte aktual unendlich kleine Summanden benutzen zu müssen, die selber wieder gebrochen sind. Wir kommen auf diese Weise so nämlich mit ganzen Zahlen im unendlich Kleinen aus und erhalten eine normierte Vorschrift, von einer Skala natürlicher oder ganzer Zahlen zur nächsten unendlich kleineren oder unendlich größeren zu gelangen. Und unser so definierter Skalenfaktor basiert auf der Menge aller endlichen Primzahlen $ \mathbb{P} $, die alle möglichen dieser Teilungen damit normiert vorgibt.
Gleichzeitig sehen wir, dass die Koeffizienten von $ \s $ in einer Fraktalebene den Nullstellen von Polynomen entsprechen, also mit elliptischen Kurven und abschließend mit algebraischen Kurven vollständig dargestellt werden können.
Strukturelle Interpretation von $ \s $ und $ ω^{ω} $
Beschäftigen wir uns mit der Entstehungsgeschichte der Menge $ \mathbb{S} $ und der echten Klasse $ \mathbb{On} $ beziehungsweise mit der Struktur der Mengen $ \left\lbrack 0, \s \right\lbrack_{\mathbb{S}_{\N}} $ und $ \left\lbrack 0, ω^{ω} \right\lbrack_{\mathbb{On}} $, dann können wir zu folgender Interpretation kommen:
Die echte Klasse der Ordinalzahlen $ \mathbb{On} $ basiert im Grunde auf dem Zählen und somit auf der Addition. Dabei wird das Symbol $ ω $ der kleinsten Unendlichkeit, der vollständigen Induktion, als unteilbar betrachtet. Dies führt dazu, dass keine weiteren arithmetischen Operation und Ganzzahligkeitsanalysen möglich sind, als die, die sich aus dem Zählen ergeben.
Anders bei $ \s $, denn $ \s $ ist als das Flächenprodukt aller endlichen Primzahlen $ ω $-ter Potenz definiert. Dadurch ergeben sich ganz andere arithmetische Operation, die zu ganzen Zahlen führen, als bei den Ordinalzahlen. So gesehen sind die Superial-Zahlen Zahlen, die im Grunde über Produkte definiert sind.
So haben wir es mit zwei Zahlensystem zu tun, die auf ganz unterschiedlichen Grundstrukturen basieren. Und erst aufgrund der Kombination beider Zahlensysteme kommen wir überhaupt in die Lage, die Anzahlen der Elemente wichtiger Zahlenmengen, wie den reell algebraischen Zahlen
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \# \left( [ 0, 1 [_{\mathbb{A}_{\S}} \right)\;\;\;=\;\;\;\frac{ \s }{ 2 ω } \;\; , } \] | () |
und die arithmetische Struktur von $ ω $, als
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { ω\;\;\;=\;\;\;2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 13 \cdot 17 \cdot 19 \cdot 23 \cdot \cdots \;\; , } \] | (SN.PP.173) |
zu verstehen, denn beide Zahlensysteme ergänzen sich auf faszinierende Weise.
| → |
|
| |
Neue Rechenregeln im Unendlichen |
|
| ← |
|
Im Aktual-Unendlichen gelten bezüglich ganzer Zahlen hier und dort ungewohnte neue Rechenregeln, mit denen wir uns etwas näher befassen.
Inhalt
| → |
|
| → |
|
| → |
|
| → |
|
Wurzeln aus aktual unendlich großen ganzen Superial-Zahlen
Wurzeln aus Summen genügend großer aktual unendlicher ganzer Superial-Zahlen sind selber ganze Superial-Zahlen.
So sind die ganzen Zahlen $ a_{s} \s^{y} $ und $ b_{s} \s^{y} $ durch den Faktor $ \s^{y} $ so groß, dass sogar aus deren Summe immer die $ y $-te Wurzel gezogen werden kann, so, dass sich immer eine ganze Superial-Zahl ergibt, was im Endlichen im Regelfall nicht gilt.
Wie wir aus dem Abschnitt ›Geschachtelte Radikale oder ihre Kehrwerte mit Summen‹ wissen,
ist eine beliebige Wurzel aus einer Summe von reell algebraischen Zahl multipliziert mit unserer superialen Basis $ \s $
eine ganze Superial-Zahl der ersten Exponentenschicht
was durch Umformung unsere Behauptung zeigt, denn die Summanden sind auch ganze Superial-Zahlen
was Voraussetzung war.
Sehr bemerkenswert auch.
Pythagoreische Tripel
Im Endlichen gibt es tatsächlich unendlich viele pythagoreische Tripel, bei denen alle drei Zahlen ganzzahlig sind. Allerdings gibt es natürlich auch sehr viele Kombinationen von ganzen Zahlen, die nicht gleich sind.
Pythagoreische Tripel im Endlichen
Pythagoreische Tripel im Superialen
Sei:
In dem Moment, wo wir sie ins Superiale skalieren
sind die superialen pythagoreischen Tripel $ a_{s} \s $, $ b_{s} \s $ und $ c_{s} \s $ für alle reell algebraischen Zahlen $ a_{s} $, $ b_{s} $ und $ c_{s} $ ganzzahlig.
So sind im Superial-Unendlichen alle pythagoreischen Tripel, deren Koordinaten reell algebraisch sind, ganzzahlig.
Und wir können verstehen, dass sie dann vor dem Hochskalieren, also im Endlichen, auf die superial kleine Exponentenschicht $ \s^{-1} $ bezogen, superial klein ganzzahlig sind und damit auf das den endlichen Zahlen unterliegende Raster fallen, dass im Kapitel ›Die arithmetische Struktur der Geometrie‹ beleuchtet wird. So ist dann auch zu verstehen, dass die Kreise mit reell algebraisch Koordinaten ebenso auf dieses Raster fallen.
Großer Fermatscher Satz
Die pythagoreischen Tripel lassen sich auf höhere Potenzen als zwei erweitern und wir landen bei den Fermatschen Tripeln und damit beim Großen Fermatschen Satz. Dieser besagt, dass es keine einzige Kombination ganzen Zahlen gibt, die die Gleichung erfüllt.
Großer Fermatscher Satz im Endlichen
Fermatsche Tripel im Superialen
Sei:
In dem Moment, wo wir es ins Superiale skalieren
sind alle superialen Fermatschen Tripel $ a_{s} \s $, $ b_{s} \s $ und $ c_{s} \s $ für alle reell algebraischen Zahlen $ a_{s} $, $ b_{s} $ und $ c_{s} $ ganz.
Bei den Fermatschen Tripeln ist bemerkenswert, dass es im Endlichen nicht eine einzige Lösung für ganze Zahlen gibt, im superialen Unendlichen sind dann alle Lösungen ganze Zahlen.
Dies hat eine gewisse Ähnlichkeit mit dem Beweis der Überrationalitätsvermutung, bei dem ganzzahlige Brüche zur Darstellung von irrationalen Wurzeln gesucht werden.
Aktual-Unendliche Exponenten der Primzahlen in Potenzzahlen
Der Beweis der Überrationalitätsvermutung bringt neue Erkenntnisse bezüglich des Rechnens mit aktual unendlichen Potenzen von Primzahlen oder allgemeiner von natürlichen Zahlen in Potenzzahlen mit sich. Diese betreffen die Ganzzahligkeit von aktual unendlichen Exponenten mit endlichen rationalen Anteilen in ihrer Summe:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \left( \forall i \in \mathbb{N} \right) \left( g \in \mathbb{N}_{\infty} \right) \left[\; i < g \;\right] } \] | (SN.ÜV.112) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}\left( \forall n \in \mathbb{N} \right) \left[\; n^{g}\;\;\;\in\;\;\;\mathbb{N}_{\infty} \;\right] } \] | (SN.ÜV.120) |
Hier steht $ g $ für jede aktual unendlich große ganze Zahl. $ n^{g} $ ist demnach dann auch eine aktual unendlich große ganze Zahl.
Dies können wir noch etwas eleganter und genauer ausdrücken, wenn wir die Klasse der wirklich aktual unendlich großen ganzen Zahlen $ \mathbb{N}_{\infty}^{\infty} $ definieren:
Nun wissen wir schon aus Formel SN.ÜV.122, dass:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \left( \forall x \in \mathbb{N}^{+} \right) \left[\; n^{g + \frac{ 1 }{ x }}\;\;\;\in\;\;\;\mathbb{N}_{\infty} \;\right] } \] | (SN.ÜV.122) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}n^{g + \frac{ 1 }{ x }}\;\;\;\in\;\;\;\mathbb{N}_{\infty}^{\infty} } \] | (SN.Ei.NR.Exp.4) |
Dann gilt auch
denn
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \left( n^{g + \frac{ 1 }{ x }} \right)^{y}\;\;\;\in\;\;\;\mathbb{N}_{\infty}^{\infty} } \] | (SN.Ei.NR.Exp.6) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \left( n^{g} \right)^{y - 1}\;\;\;\in\;\;\;\mathbb{N}_{\infty}^{\infty} } \] | (SN.Ei.NR.Exp.7) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { n^{g + \frac{ y }{ x }}\;\;\;=\;\;\;\frac{ \left( n^{g + \frac{ 1 }{ x }} \right)^{y} }{ \left( n^{g} \right)^{y - 1} } } \] | (SN.Ei.NR.Exp.8) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}n^{g + \frac{ y }{ x }}\;\;\;=\;\;\;\frac{ n^{y g + \frac{ y }{ x }} }{ n^{(y - 1) g} } } \] | (SN.Ei.NR.Exp.9) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}n^{g + \frac{ y }{ x }}\;\;\;=\;\;\;n^{\left( y g + \frac{ y }{ x } \right) - (y - 1) g} } \] | (SN.Ei.NR.Exp.10) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}n^{g + \frac{ y }{ x }}\;\;\;=\;\;\;n^{y g - (y - 1) g + \frac{ y }{ x }} } \] | (SN.Ei.NR.Exp.11) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}n^{g + \frac{ y }{ x }}\;\;\;=\;\;\;n^{g + \frac{ y }{ x }} \;\; . } \] | (SN.Ei.NR.Exp.12) | ||
| ▾ | In faktorisierter Form: |
Die ganzzahlige Teilbarkeit des Bruchs wird durch die um $ y $ erhöhte Potenz des Zähler garantiert, im Verhältnis zu der die Erhöhung der Potenz des Nenners mit $ y - 1 $ geringer ausfällt.
Betrachtung im Rahmen der Potenzialzahlen
Die Potenzialzahlen $ \mathbb{Pn} $ sind Zahlen, die im Allgemeinen nicht in der Menge der Superial-Zahlen $ \mathbb{S} $ und auch nicht in der Klasse der Ordinalzahlen $ \mathbb{On} $ sind. Sie spielen beim Beweis der Überrationalitätsvermutung eine entscheidende Rolle, der für die Superial-Zahlen sehr bedeutsam ist, und ergänzen die vorgenannte Klasse und Menge systematisch.
Sie sind Potenzen natürlicher Zahlen beziehungsweise von Primzahlen, die bis zur vollständigen Induktion $ ω $ und noch weiter hinauf reichen und Summen dieser. Die aktual unendliche Größe $ g $ in den obigen allgemeinen Rechenregeln ist bei den Potenzialzahlen durch positive natürliche Potenzen von $ ω $ und deren positive natürliche Vielfache ersetzt.
So sind die Potenzialzahlen diesbezüglich einfach ein Spezialfall.
| → |
|
| |
Vergleich mit hyperreellen Zahlen |
|
| ← |
|
| ▾ | Notizen |
• Die Null ist in den Superial-Zahlen viel simpler definiert, als in den hyperreellen Zahlen.
• In den Superial-Zahlen brauchen wir nicht eine Reihe von unendlich vielen Zahlen, um infinite und infinitesimale Zahlen zu definieren.
– Wir können das Symbol $ \s $ für ein unendliches Flächenprodukt der Primzahlen nehmen, siehe oben, und dieses mit endlichen Symbolen, wie Brüchen, kombinieren.
(In Arbeit …)
(In Arbeit …)
(In Arbeit …)
| → |
|
| |
Untersuchungen zur Kontinuumshypothese |
|
Die Mächtigkeit der reellen Zahlen
| ← |
|
| ▾ | Notizen |
• Verweisen auf Die arithmetische Struktur der Geometrie.
Die Mächtigkeit der reellen Zahlen wird mit $ \mathfrak{c} $ bezeichnet:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \mathfrak{c}\;\;\;=\;\;\;\left| \mathbb{R} \right| } \] | (SN.Eig.UK.1) |
Wäre die Kontinuumshypothese wahr, dann könnte gezeigt werden, dass die Mächtigkeit des Kontinuums der Potenzmenge von $ \mathbb{N} $ entspricht. Warum die Kontinuumshypothese genau dies annimmt, hab ich noch nicht ganz genau verstanden. Die Mächtigkeit des Kontinuums wird dann mit Hilfe von $ ω $ als $ \aleph_{1} $ formuliert:
Die Kontinuumshypothese vermutet, dass die reellen Zahlen die gleiche Mächtigkeit besitzen, wie das Kontinuum:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \mathfrak{c}\;\;\;\overset{?}{=}\;\;\;\aleph_{1} } \] | (SN.Eig.UK.5) |
Die Idee ist also, dass die Mächtigkeit der reellen Zahlen der Mächtigkeit der Potenzmenge der Menge $ \mathbb{N} $ der natürlichen Zahlen, also $ \vert \mathcal{P}(\mathbb{N}) \vert $, mit $ 2^{ω} $ entspricht. Die Mächtigkeit einer Menge ist dabei nicht unbedingt der Anzahl der Elemente dieser Menge gleich.
Dies möchte ich nicht bezüglich der Mächtigkeit grundsätzlich in Frage stellen. Sondern ich möchte die Kontinuumshypothese durch die mit den Superial-Zahlen gefundene Struktur des Unendlichen, der Dichte oder das Rasters der arithmetischen Struktur der Geometrie, differenzierter und tiefer beleuchten sowie gegebenenfalls sinnvoller formulieren, um weitere Erkenntnisse zu gewinnen.
Mit der Kontinuumshypothese wird angenommen:
» Es gibt keine Menge, deren Mächtigkeit zwischen der Mächtigkeit der natürlichen Zahlen und der Mächtigkeit der reellen Zahlen liegt. «
Dies soll erst einmal so stehen bleiben, weil es hier nicht direkt um den Beweis oder die Widerlegung der Kontinuumshypothese geht.
Es soll vorerst darum gehen, die Struktur der Zahlen, bestenfalls der reellen Zahlen, tiefer zu beleuchten, um zu sehen, ob und, wenn ja, welche Erkenntnisse sich diesbezüglich ergeben.
Die Potenz $ 2^{ω} $ ist uns aus dem Primzahl-Flächenprodukt bereits bekannt
Die von uns bewiesene Primzahlprodukt-Vermutung zeigt, dass die Anzahl aller endlichen natürlichen Zahlen $ ω $ im Primzahl-Flächenprodukt zu finden ist. Und zwar in der Zeile, die das Produkt aller endlichen Primzahlen darstellt:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { ω\;\;\;=\;\;\;2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 13 \cdot 17 \cdot 19 \cdot 23 \cdot \cdots } \] | (SN.PP.173) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \s\;\;\;=\;\;\;ω^{ω} } \] | (SN.PP.174) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\s\;\;\;=\;\;\;\left( 2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 13 \cdot 17 \cdot 19 \cdot 23 \cdot \cdots \right)^{ω} } \] | (SN.Ein.29) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\s\;\;\;=\;\;\;2^{ω} \cdot 3^{ω} \cdot 5^{ω} \cdot 7^{ω} \cdot 11^{ω} \cdot 13^{ω} \cdot 17^{ω} \cdot 19^{ω} \cdot 23^{ω} \cdot \cdots } \] | (SN.Eig.UK.6) |
Wir sehen die Potenz $ 2^{ω} $ als ersten Primzahlturm im Produkt von $ \s $.
Weiterhin ergibt sich die neue Erkenntnis, dass $ \aleph_{1} $ in seiner Potenz von $ 2 $ im Exponenten das Produkt aller Primzahlen enthält:
Dies sind Formulierungen, die neu sind, soweit mir bekannt.
Die Konstruktion und der Sinn von $ \s $ wirft Fragen bezüglich der Struktur der reellen Zahlen auf
Nun geht es bei der Kontinuumshypothese auch um die Mächtigkeit der reellen Zahlen und um die der natürlichen Zahlen; schließlich ja um die Frage, ob es noch eine Mächtigkeit zwischen denen dieser beiden Mengen gibt.
Die superiale Basis $ \s $ ist nun so konstruiert, dass ein Produkt mit ihr und jeder reell algebraischen Zahl, die durch Radikale darstellbar ist, eine ganze Zahl ergibt, wie wir im Abschnitt ›Die sinnvollen Koeffizienten der Superial-Zahlen‹ zeigen. Dies gelingt unter anderem mit Hilfe unseres Beweises der Überrationalitätsvermutung. Und wir vermuten, dass dies sogar für alle reell algebraischen Zahlen gilt, was allerdings noch zu beweisen aussteht.
Es ist offensichtlich, dass jedes Produkt einer rationalen Zahl mit unserer superialen Basis $ \s $ eine ganze Zahl ergibt. Wir können daran erkennen, dass schon die Struktur der reell algebraischen Zahlen es erfordert, nicht nur $ 2^{ω} $, sondern auch $ 3^{ω} $ und ebenso alle anderen aktual unendlichen Potenzen endlicher Primzahlen bis ins Unendliche, einzubeziehen. Da scheint es Fraglich, ob $ 2^{ω} $ ausreichen kann, die Komplexität oder Feinheit der Struktur aller reellen Zahlen darzustellen. Dazu kommt, dass die reellen Zahlen auch noch alle transzendenten Zahlen enthalten sollen, was im Rahmen der Superial-Zahlen weitere interessante Fragen aufwirft, siehe Seite ›Superiale-Transzendenz-Vermutung‹ oder auch den folgenden Abschnitt ›‹.
Während die Mächtigkeit der reell algebraischen Zahlen, der der natürlichen Zahlen entspricht, weil sie abzählbar sind, ist die Mächtigkeit der transzendenten Zahlen überabzählbar.
Durch die Superial-Zahlen sehen wir nun, dass die Anzahl der sinnvollen Koeffizienten der Superial-Zahlen $ \# \mathbb{A}_{\S} $ dem besagten aktual unendlichen Flächenprodukt $ \s $ geteilt durch die Anzahl der endlichen ganzen Zahlen $ \# \mathbb{Z} = 2 \cdot ω $, also $ \# \mathbb{A}_{\S} = \frac{ \s }{ 2 \cdot ω } $, entspricht, siehe Formel .
Wenn wir dies alles in einer Gesamtschau betrachten, bekomme ich den Eindruck, dass hier etwas nicht zusammenpasst und überdacht werden sollte.
Unabhängigkeit von der Mengenlehre (ZFC)
An dieser Stelle möchte ich darauf aufmerksam machen, dass die Kontinuumshypothese von der
Zermelo-Fraenkel-Mengenlehre mit Auswahlaxiom (ZFC) insgesamt unabhängig ist.
Dass bedeutet, die Mengenlehre – genauer die ZFC-Mengenlehre – gibt uns nicht die Möglichkeit zu entscheiden, ob die Kontinuumshypothese wahr oder falsch ist.
Hier kommen die auf diesen Seiten entwickelten Superial-Zahlen, und die mit ihnen verbundenen Biordinalzahlen, ins Spiel. Die Superial-Zahlen begründen das Aktual-Unendliche auf den endlichen Primzahlen und so auf der Arithmetik und bringen sie mit der Mengenlehre zusammen. Sie erweitern so die reell algebraischen Zahlen, die durch Radikale darstellbar sind, und vielleicht sogar alle, auf einen aktual unendlichen angeordneten algebraischen Körper,. Das heißt, wir haben durch die Superial-Zahlen nicht nur die Mengenlehre, sondern auch eine Arithmetik des Aktual-Unendlichen mit ausgezeichneten Eigenschaften zur Verfügung.
Und dadurch konnten wir schon neue Erkenntnisse der Arithmetik des Aktual-Unendlichen gewinnen, wie eine neue Definition der Ableitung, des Integrals, also der Erweiterung des Zählens, und der Primzahlen, der Definition der vollständigen Induktion über endliche Primzahlen sowie der Definition von irrationalen reell algebraischen Zahlen mit überratiionalen Brüchen, also Brüchen aus aktual unendlichen ganzen Zahlen, die irrationale Wurzeln und ähnliches beschreiben.
All dies steht offensichtlich in Beziehung zur Kontinuumshypothese und kann so zu deren besseren Verständnis herangezogen werden.
Transzendente Zahlen
Hinsichtlich der transzendenten Zahlen möchte ich am Beispiel der superialen Eulerschen Zahl $ \e_\s $ zeigen, dass sich hier weitere Fragen ergeben:
Auf der Seite Die eulersche Zahl e und ihre Exponentialfunktion kommen wir zu dem Schluss, dass die Eulersche Zahl keine rein endliche irrationale Zahl ist, nicht einmal eine Superial-Zahl der auf dieser Seite definierten 1. Ordnung, weil sie unweigerlich aktual unendlich kleine Summanden der Größenordnung $ \s^{-\s} $ enthält, die nicht Null werden können. Wie gesagt, fällt sie hierdurch selbst aus der Menge $ \mathbb{S} $ der Superial-Zahlen heraus. Sie ist also keine rein endliche reelle Zahl, die nur aus Summanden endlicher Größe besteht.
An dieser Stelle würde ich sagen, dass zumindestens $ \e_\s $ keine reelle Zahl ist und die Frage im Raum steht, ob nicht auch alle anderen transzendenten Zahlen eigentlich gar keine reellen Zahlen sind. Sondern, wir lassen uns vielleicht dadurch täuschen, dass wir glauben, transzendente Zahlen wären durch Dezimalzahlen mit unendlich vielen Nachkommastellen darstellbar, ohne zu beantworten, wie groß diese minimale Unendlichkeit der Nachkommastellen denn eigentlich ist; ob es nicht vielleicht unendliche Größenordnungen mehr sind, als die Unendlichkeit der vollständigen Induktion, also $ \s = ω^{ω} $ viele Nachkommastellen.
Schlussfolgerung zur Untersuchung der Kontinuumshypothese
Ich denke, wir sollten die Struktur der reellen Zahlen und ihre Aufteilung in Untermengen mit Hilfe der Primzahlen – und somit mit Hilfe der Superial-Zahlen – tiefer untersuchen und verstehen, damit wir in die Lage kommen, die Kontinuumshypothese im Detail zu beleuchten und hoffentlich dann für uns sinnvolle Antworten zu finden.
| → |
| |
Fußnoten |
|
| 1. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Abelsche Gruppe. | |
| 2. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Ordinalzahl. | |
| 3. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Algebraische Zahl. | |
| 4. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Transzendente Zahl. | |
| 5. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Lexikographische Ordnung. Vgl. Wikipedia, Stellenwertsystem, Lexikographische Ordnung. | |
| 6. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Geordneter Körper. | |
| 7. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Geordneter Körper, Strukturaussagen. Vgl. Wikipedia, Archimedisches Axiom. | |
| 8. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Archimedisches Axiom. | |
| 9. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Ordinalzahl. | |
| 10. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Ring (Algebra). | |
| 11. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Vollständige Induktion, Das Axiom der vollständigen Induktion. Vgl. Wikipedia, Unendlichkeitsaxiom, Formulierung; Bedeutung für die Mathematik, Natürliche Zahlen. | |
| 12. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Ordinalzahl. | |
| 13. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Stellenwertsystem. | |
| 14. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Riemannsche Vermutung. | |
| 15. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Ordinalzahl. | |
| 16. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Klasse (Mengenlehre), Echte Klassen. | |
| 17. |
Alle Ordinalzahlen als Ganzes ist eine echte Klasse und keine(!) Menge: (Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Ordinalzahl. | |
| 18. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Ordinalzahl, Motivation und Definition, Limes- und Nachfolgerzahlen. | |
| 19. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Gaußsche Summenformel. | |
| 20. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Vollständige Induktion, Das Axiom der vollständigen Induktion. Vgl. Wikipedia, Unendlichkeitsaxiom, Formulierung; Bedeutung für die Mathematik, Natürliche Zahlen. | |
| 21. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Elliptische Kurve. | |
| 22. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Algebraische Kurve. | |
| 23. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Vollständige Induktion, Das Axiom der vollständigen Induktion. Vgl. Wikipedia, Unendlichkeitsaxiom, Formulierung; Bedeutung für die Mathematik, Natürliche Zahlen. | |
| 24. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Pythagoreisches Tripel. | |
| 25. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Großer Fermatscher Satz. | |
| 26. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Ordinalzahl. | |
| 27. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Vollständige Induktion, Das Axiom der vollständigen Induktion. Vgl. Wikipedia, Unendlichkeitsaxiom, Formulierung; Bedeutung für die Mathematik, Natürliche Zahlen. | |
| 28. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Mächtigkeit. | |
| 29. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Kontinuumshypothese, Aussage, Einfache Kontinuumshypothese. | |
| 30. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Kontinuumshypothese. | |
| 31. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Kontinuumshypothese, Aussage, Einfache Kontinuumshypothese. | |
| 32. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Kontinuumshypothese, Aussage, Einfache Kontinuumshypothese. | |
| 33. |
Internet: Wikipedia, Kontinuumshypothese, Aussage. | |
| 34. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Algebraische Zahl, Eigenschaften. | |
| 35. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Transzendente Zahl. | |
| 36. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Transzendente Zahl, Überabzählbarkeit. | |
| 37. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Kontinuumshypothese, Unabhängigkeit von ZFC. | |
| 38. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Körper (Algebra). | |
| 39. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Algebraischer Zahlkörper. |
| |
Stand 20. November 2025, 23:00 CET.
-
Permanente Links:
(Klicke auf die Archivlogos
zum Abruf und Ansehen
der Archive dieser Seite.) -

-
archive.todaywebpage capture